Consensus Learning with Deep Sets for Essential Matrix Estimation

Robust estimation of the essential matrix, which encodes the relative position and orientation of two cameras, is a fundamental step in structure from motion pipelines. Recent deep-based methods achieved accurate estimation by using complex network architectures that involve graphs, attention layers, and hard pruning steps. Here, we propose a simpler network architecture based on Deep Sets. Given a collection of point matches extracted from two images, our method identifies outlier point matches and models the displacement noise in inlier matches. A weighted DLT module uses these predictions to regress the essential matrix. Our network achieves accurate recovery that is superior to existing networks with significantly more complex architectures.

CinePile: A Long Video Question Answering Dataset and Benchmark

Current datasets for long-form video understanding often fall short of providing genuine long-form comprehension challenges, as many tasks derived from these datasets can be successfully tackled by analyzing just one or a few random frames from a video. To address this issue, we present a novel dataset and benchmark, CinePile, specifically designed for authentic long-form video understanding. This paper details our innovative approach for creating a question-answer dataset, utilizing advanced LLMs with human-in-the-loop and building upon human-generated raw data. Our comprehensive dataset comprises 305,000 multiple-choice questions (MCQs), covering various visual and multimodal aspects, including temporal comprehension, understanding human-object interactions, and reasoning about events or actions within a scene. Additionally, we evaluate recent video-centric LLMs, both open-source and proprietary, on the test split of our dataset. The findings reveal that even state-of-the-art video-centric LLMs significantly lag behind human performance in these tasks, highlighting the complexity and challenge inherent in video understanding. The dataset is available at https://hf.co/datasets/tomg-group-umd/cinepile

RESFM: Robust Equivariant Multiview Structure from Motion

Multiview Structure from Motion is a fundamental and challenging computer vision problem. A recent deep-based approach was proposed utilizing matrix equivariant architectures for the simultaneous recovery of camera pose and 3D scene structure from large image collections. This work however made the unrealistic assumption that the point tracks given as input are clean of outliers. Here we propose an architecture suited to dealing with outliers by adding an inlier/outlier classifying module that respects the model equivariance and by adding a robust bundle adjustment step. Experiments demonstrate that our method can be successfully applied in realistic settings that include large image collections and point tracks extracted with common heuristics and include many outliers.

Controlling the Inductive Bias of Wide Neural Networks by Modifying the Kernel's Spectrum

Wide neural networks are biased towards learning certain functions, influencing both the rate of convergence of gradient descent (GD) and the functions that are reachable with GD in finite training time. As such, there is a great need for methods that can modify this bias according to the task at hand. To that end, we introduce Modified Spectrum Kernels (MSKs), a novel family of constructed kernels that can be used to approximate kernels with desired eigenvalues for which no closed form is known. We leverage the duality between wide neural networks and Neural Tangent Kernels and propose a preconditioned gradient descent method, which alters the trajectory of GD. As a result, this allows for a polynomial and, in some cases, exponential training speedup without changing the final solution. Our method is both computationally efficient and simple to implement.

GRelPose: Generalizable End-to-End Relative Camera Pose Regression

This paper proposes a generalizable, end-to-end deep learning-based method for relative pose regression between two images. Given two images of the same scene captured from different viewpoints, our algorithm predicts the relative rotation and translation between the two respective cameras. Despite recent progress in the field, current deep-based methods exhibit only limited generalization to scenes not seen in training. Our approach introduces a network architecture that extracts a grid of coarse features for each input image using the pre-trained LoFTR network. It subsequently relates corresponding features in the two images, and finally uses a convolutional network to recover the relative rotation and translation between the respective cameras. Our experiments indicate that the proposed architecture can generalize to novel scenes, obtaining higher accuracy than existing deep-learning-based methods in various settings and datasets, in particular with limited training data.

A Kernel Perspective of Skip Connections in Convolutional Networks

Over-parameterized residual networks (ResNets) are amongst the most successful convolutional neural architectures for image processing. Here we study their properties through their Gaussian Process and Neural Tangent kernels. We derive explicit formulas for these kernels, analyze their spectra, and provide bounds on their implied condition numbers. Our results indicate that (1) with ReLU activation, the eigenvalues of these residual kernels decay polynomially at a similar rate compared to the same kernels when skip connections are not used, thus maintaining a similar frequency bias; (2) however, residual kernels are more locally biased. Our analysis further shows that the matrices obtained by these residual kernels yield favorable condition numbers at finite depths than those obtained without the skip connections, enabling therefore faster convergence of training with gradient descent.

On the Spectral Bias of Convolutional Neural Tangent and Gaussian Process Kernels

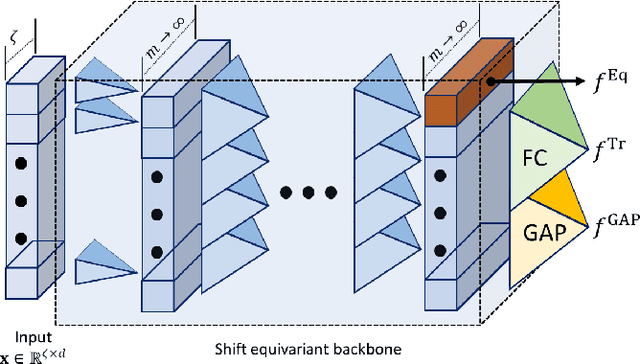
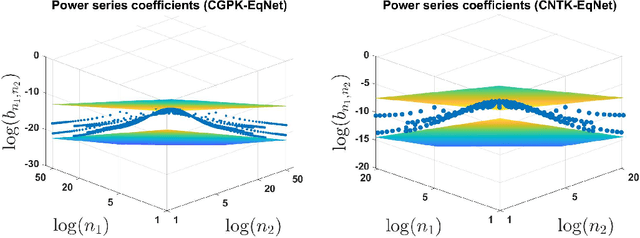
We study the properties of various over-parametrized convolutional neural architectures through their respective Gaussian process and neural tangent kernels. We prove that, with normalized multi-channel input and ReLU activation, the eigenfunctions of these kernels with the uniform measure are formed by products of spherical harmonics, defined over the channels of the different pixels. We next use hierarchical factorizable kernels to bound their respective eigenvalues. We show that the eigenvalues decay polynomially, quantify the rate of decay, and derive measures that reflect the composition of hierarchical features in these networks. Our results provide concrete quantitative characterization of over-parameterized convolutional network architectures.

Deep Permutation Equivariant Structure from Motion

Existing deep methods produce highly accurate 3D reconstructions in stereo and multiview stereo settings, i.e., when cameras are both internally and externally calibrated. Nevertheless, the challenge of simultaneous recovery of camera poses and 3D scene structure in multiview settings with deep networks is still outstanding. Inspired by projective factorization for Structure from Motion (SFM) and by deep matrix completion techniques, we propose a neural network architecture that, given a set of point tracks in multiple images of a static scene, recovers both the camera parameters and a (sparse) scene structure by minimizing an unsupervised reprojection loss. Our network architecture is designed to respect the structure of the problem: the sought output is equivariant to permutations of both cameras and scene points. Notably, our method does not require initialization of camera parameters or 3D point locations. We test our architecture in two setups: (1) single scene reconstruction and (2) learning from multiple scenes. Our experiments, conducted on a variety of datasets in both internally calibrated and uncalibrated settings, indicate that our method accurately recovers pose and structure, on par with classical state of the art methods. Additionally, we show that a pre-trained network can be used to reconstruct novel scenes using inexpensive fine-tuning with no loss of accuracy.

Spectral Analysis of the Neural Tangent Kernel for Deep Residual Networks

Deep residual network architectures have been shown to achieve superior accuracy over classical feed-forward networks, yet their success is still not fully understood. Focusing on massively over-parameterized, fully connected residual networks with ReLU activation through their respective neural tangent kernels (ResNTK), we provide here a spectral analysis of these kernels. Specifically, we show that, much like NTK for fully connected networks (FC-NTK), for input distributed uniformly on the hypersphere $\mathbb{S}^{d-1}$, the eigenfunctions of ResNTK are the spherical harmonics and the eigenvalues decay polynomially with frequency $k$ as $k^{-d}$. These in turn imply that the set of functions in their Reproducing Kernel Hilbert Space are identical to those of FC-NTK, and consequently also to those of the Laplace kernel. We further show, by drawing on the analogy to the Laplace kernel, that depending on the choice of a hyper-parameter that balances between the skip and residual connections ResNTK can either become spiky with depth, as with FC-NTK, or maintain a stable shape.

Shift Invariance Can Reduce Adversarial Robustness

Shift invariance is a critical property of CNNs that improves performance on classification. However, we show that invariance to circular shifts can also lead to greater sensitivity to adversarial attacks. We first characterize the margin between classes when a shift-invariant linear classifier is used. We show that the margin can only depend on the DC component of the signals. Then, using results about infinitely wide networks, we show that in some simple cases, fully connected and shift-invariant neural networks produce linear decision boundaries. Using this, we prove that shift invariance in neural networks produces adversarial examples for the simple case of two classes, each consisting of a single image with a black or white dot on a gray background. This is more than a curiosity; we show empirically that with real datasets and realistic architectures, shift invariance reduces adversarial robustness. Finally, we describe initial experiments using synthetic data to probe the source of this connection.