Javier Morales
Improving Content Recommendation: Knowledge Graph-Based Semantic Contrastive Learning for Diversity and Cold-Start Users
Mar 27, 2024Abstract:Addressing the challenges related to data sparsity, cold-start problems, and diversity in recommendation systems is both crucial and demanding. Many current solutions leverage knowledge graphs to tackle these issues by combining both item-based and user-item collaborative signals. A common trend in these approaches focuses on improving ranking performance at the cost of escalating model complexity, reducing diversity, and complicating the task. It is essential to provide recommendations that are both personalized and diverse, rather than solely relying on achieving high rank-based performance, such as Click-through Rate, Recall, etc. In this paper, we propose a hybrid multi-task learning approach, training on user-item and item-item interactions. We apply item-based contrastive learning on descriptive text, sampling positive and negative pairs based on item metadata. Our approach allows the model to better understand the relationships between entities within the knowledge graph by utilizing semantic information from text. It leads to more accurate, relevant, and diverse user recommendations and a benefit that extends even to cold-start users who have few interactions with items. We perform extensive experiments on two widely used datasets to validate the effectiveness of our approach. Our findings demonstrate that jointly training user-item interactions and item-based signals using synopsis text is highly effective. Furthermore, our results provide evidence that item-based contrastive learning enhances the quality of entity embeddings, as indicated by metrics such as uniformity and alignment.
Leveraging Unlabeled Data for Sketch-based Understanding
Apr 26, 2022



Abstract:Sketch-based understanding is a critical component of human cognitive learning and is a primitive communication means between humans. This topic has recently attracted the interest of the computer vision community as sketching represents a powerful tool to express static objects and dynamic scenes. Unfortunately, despite its broad application domains, the current sketch-based models strongly rely on labels for supervised training, ignoring knowledge from unlabeled data, thus limiting the underlying generalization and the applicability. Therefore, we present a study about the use of unlabeled data to improve a sketch-based model. To this end, we evaluate variations of VAE and semi-supervised VAE, and present an extension of BYOL to deal with sketches. Our results show the superiority of sketch-BYOL, which outperforms other self-supervised approaches increasing the retrieval performance for known and unknown categories. Furthermore, we show how other tasks can benefit from our proposal.
Traditional and accelerated gradient descent for neural architecture search
Jul 02, 2020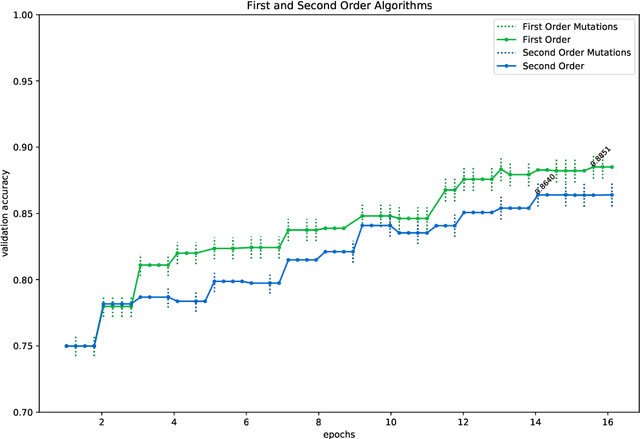
Abstract:In this paper, we introduce two algorithms for neural architecture search (NASGD and NASAGD) following the theoretical work by two of the authors [4], which aimed at introducing the conceptual basis for new notions of traditional and accelerated gradient descent algorithms for the optimization of a function on a semi-discrete space using ideas from optimal transport theory. Our methods, which use the network morphism framework introduced in [3] as a baseline, can analyze forty times as many architectures as the hill climbing methods [3,11] while using the same computational resources and time and achieving comparable levels of accuracy. For example, using NASGD on CIFAR-10, our method designs and trains networks with an error rate of 4.06 in only 12 hours on a single GPU.
Semi-discrete optimization through semi-discrete optimal transport: a framework for neural architecture search
Jun 26, 2020Abstract:In this paper we introduce a theoretical framework for semi-discrete optimization using ideas from optimal transport. Our primary motivation is in the field of deep learning, and specifically in the task of neural architecture search. With this aim in mind, we discuss the geometric and theoretical motivation for new techniques for neural architecture search (in the companion work \cite{practical}; we show that algorithms inspired by our framework are competitive with contemporaneous methods). We introduce a Riemannian like metric on the space of probability measures over a semi-discrete space $\mathbb{R}^d \times \mathcal{G}$ where $\mathcal{G}$ is a finite weighted graph. With such Riemmanian structure in hand, we derive formal expressions for the gradient flow of a relative entropy functional, as well as second order dynamics for the optimization of said energy. Then, with the aim of providing a rigorous motivation for the gradient flow equations derived formally we also consider an iterative procedure known as minimizing movement scheme (i.e., Implicit Euler scheme, or JKO scheme) and apply it to the relative entropy with respect to a suitable cost function. For some specific choices of metric and cost, we rigorously show that the minimizing movement scheme of the relative entropy functional converges to the gradient flow process provided by the formal Riemannian structure. This flow coincides with a system of reaction-diffusion equations on $\mathbb{R}^d$.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge