Puzzle: Distillation-Based NAS for Inference-Optimized LLMs

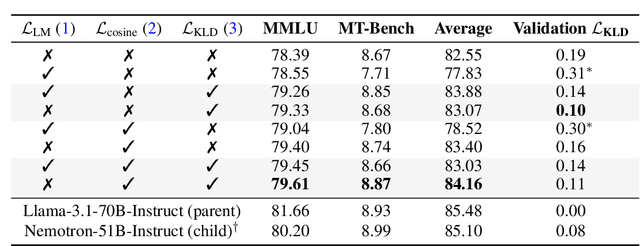
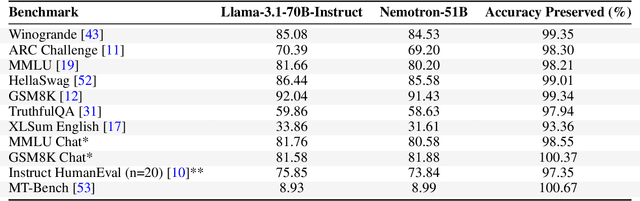
Large language models (LLMs) have demonstrated remarkable capabilities, but their adoption is limited by high computational costs during inference. While increasing parameter counts enhances accuracy, it also widens the gap between state-of-the-art capabilities and practical deployability. We present Puzzle, a framework to accelerate LLM inference on specific hardware while preserving their capabilities. Through an innovative application of neural architecture search (NAS) at an unprecedented scale, Puzzle systematically optimizes models with tens of billions of parameters under hardware constraints. Our approach utilizes blockwise local knowledge distillation (BLD) for parallel architecture exploration and employs mixed-integer programming for precise constraint optimization. We demonstrate the real-world impact of our framework through Llama-3.1-Nemotron-51B-Instruct (Nemotron-51B), a publicly available model derived from Llama-3.1-70B-Instruct. Nemotron-51B achieves a 2.17x inference throughput speedup, fitting on a single NVIDIA H100 GPU while preserving 98.4% of the original model's capabilities. Nemotron-51B currently stands as the most accurate language model capable of inference on a single GPU with large batch sizes. Remarkably, this transformation required just 45B training tokens, compared to over 15T tokens used for the 70B model it was derived from. This establishes a new paradigm where powerful models can be optimized for efficient deployment with only negligible compromise of their capabilities, demonstrating that inference performance, not parameter count alone, should guide model selection. With the release of Nemotron-51B and the presentation of the Puzzle framework, we provide practitioners immediate access to state-of-the-art language modeling capabilities at significantly reduced computational costs.

SelectiveNet: A Deep Neural Network with an Integrated Reject Option

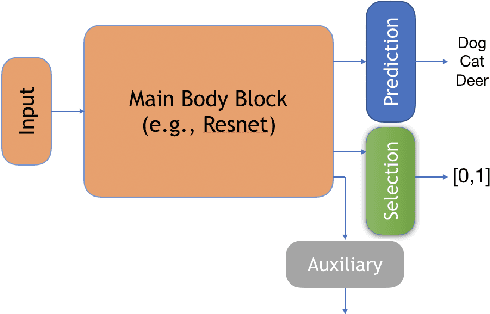
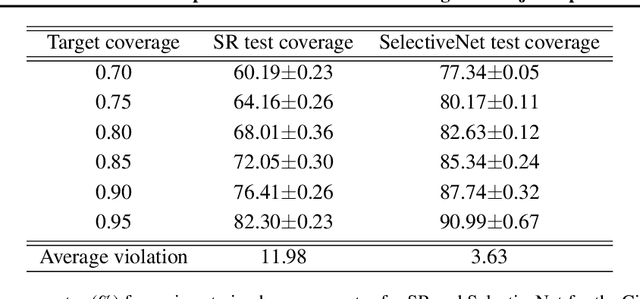
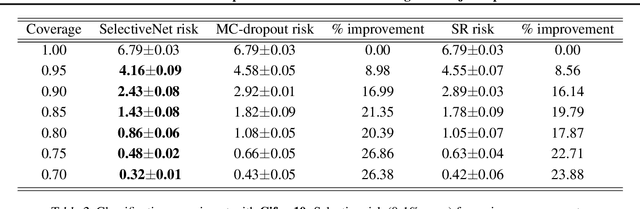
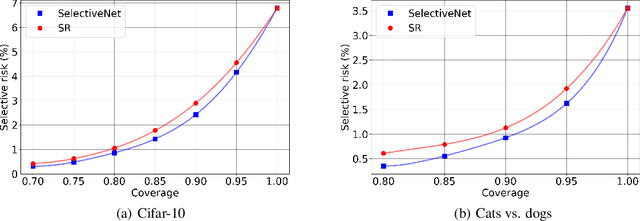
We consider the problem of selective prediction (also known as reject option) in deep neural networks, and introduce SelectiveNet, a deep neural architecture with an integrated reject option. Existing rejection mechanisms are based mostly on a threshold over the prediction confidence of a pre-trained network. In contrast, SelectiveNet is trained to optimize both classification (or regression) and rejection simultaneously, end-to-end. The result is a deep neural network that is optimized over the covered domain. In our experiments, we show a consistently improved risk-coverage trade-off over several well-known classification and regression datasets, thus reaching new state-of-the-art results for deep selective classification.

Deep Active Learning with a Neural Architecture Search

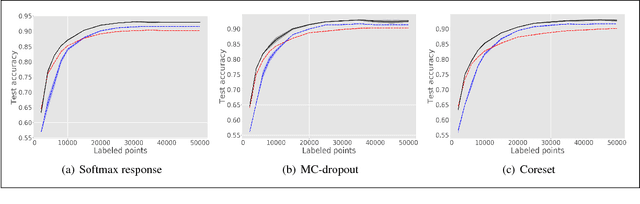
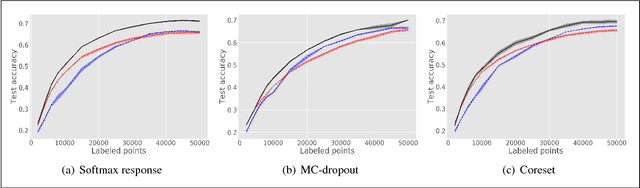
We consider active learning of deep neural networks. Most active learning works in this context have focused on studying effective querying mechanisms and assumed that an appropriate network architecture is a priori known for the problem at hand. We challenge this assumption and propose a novel active strategy whereby the learning algorithm searches for effective architectures on the fly, while actively learning. We apply our strategy using three known querying techniques (softmax response, MC-dropout, and coresets) and show that the proposed approach overwhelmingly outperforms active learning using fixed architectures.

Bias-Reduced Uncertainty Estimation for Deep Neural Classifiers

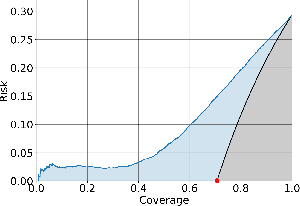
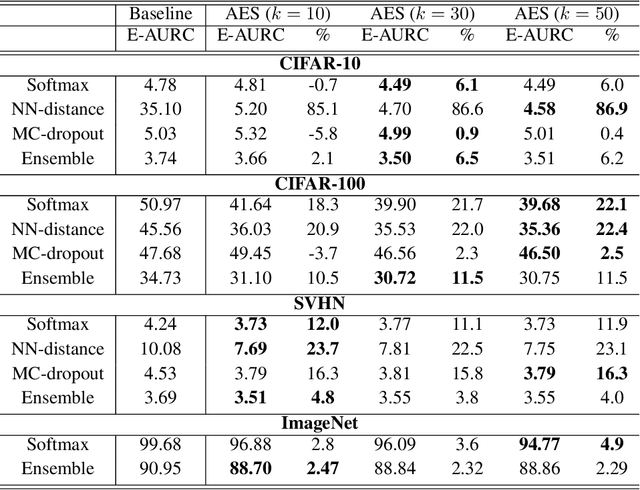
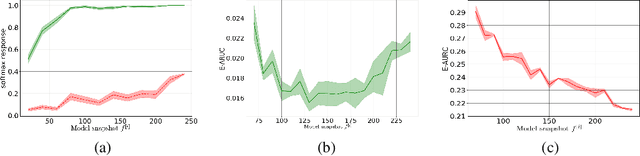
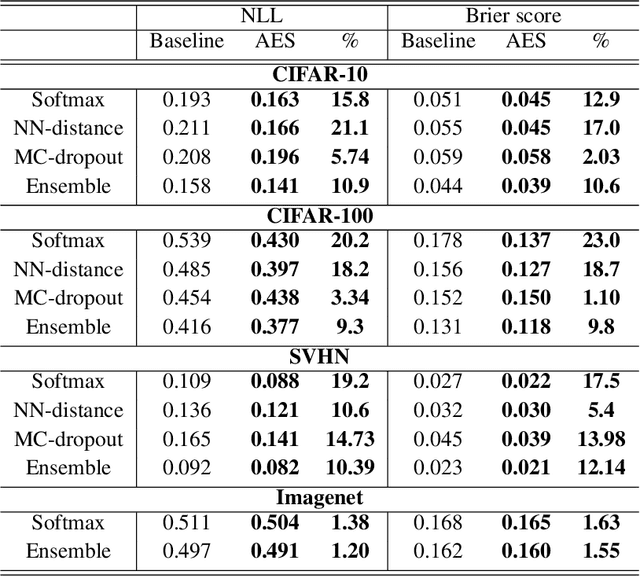
We consider the problem of uncertainty estimation in the context of (non-Bayesian) deep neural classification. In this context, all known methods are based on extracting uncertainty signals from a trained network optimized to solve the classification problem at hand. We demonstrate that such techniques tend to introduce biased estimates for instances whose predictions are supposed to be highly confident. We argue that this deficiency is an artifact of the dynamics of training with SGD-like optimizers, and it has some properties similar to overfitting. Based on this observation, we develop an uncertainty estimation algorithm that selectively estimates the uncertainty of highly confident points, using earlier snapshots of the trained model, before their estimates are jittered (and way before they are ready for actual classification). We present extensive experiments indicating that the proposed algorithm provides uncertainty estimates that are consistently better than all known methods.

Deep Active Learning over the Long Tail

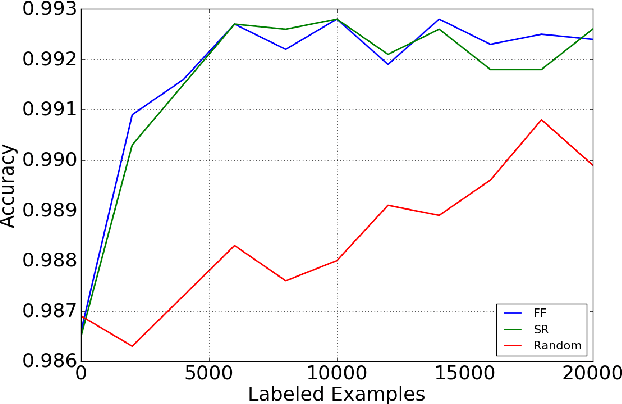
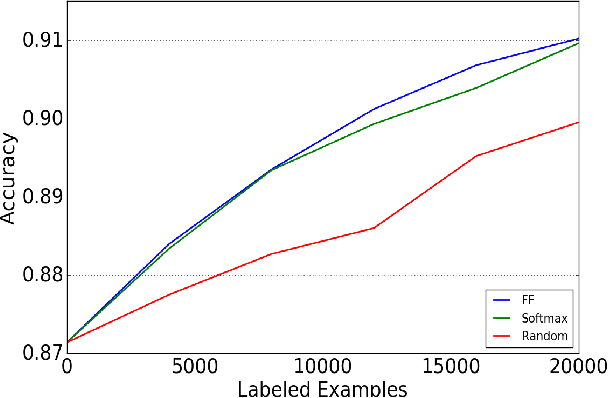
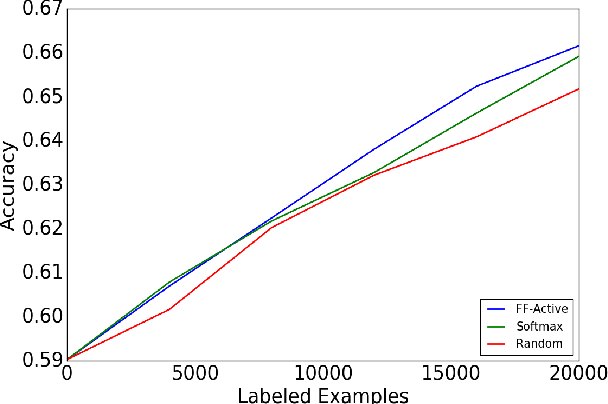
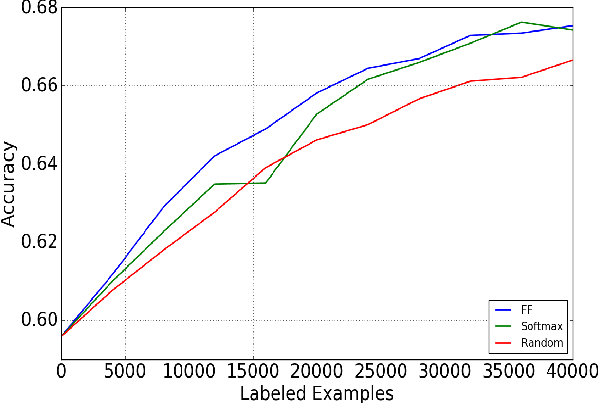
This paper is concerned with pool-based active learning for deep neural networks. Motivated by coreset dataset compression ideas, we present a novel active learning algorithm that queries consecutive points from the pool using farthest-first traversals in the space of neural activation over a representation layer. We show consistent and overwhelming improvement in sample complexity over passive learning (random sampling) for three datasets: MNIST, CIFAR-10, and CIFAR-100. In addition, our algorithm outperforms the traditional uncertainty sampling technique (obtained using softmax activations), and we identify cases where uncertainty sampling is only slightly better than random sampling.

Selective Classification for Deep Neural Networks

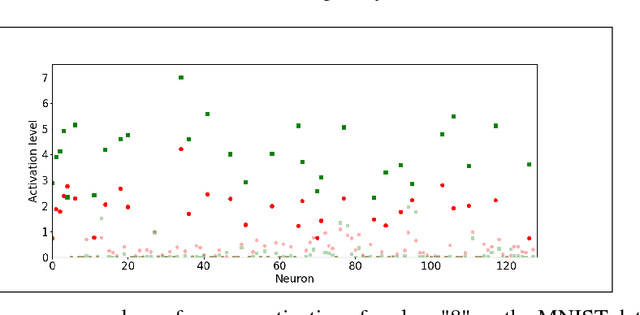
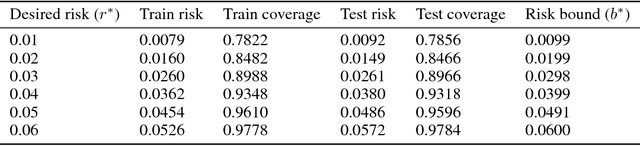
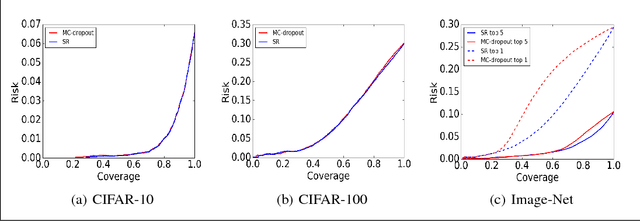
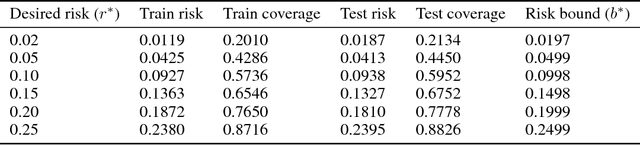
Selective classification techniques (also known as reject option) have not yet been considered in the context of deep neural networks (DNNs). These techniques can potentially significantly improve DNNs prediction performance by trading-off coverage. In this paper we propose a method to construct a selective classifier given a trained neural network. Our method allows a user to set a desired risk level. At test time, the classifier rejects instances as needed, to grant the desired risk (with high probability). Empirical results over CIFAR and ImageNet convincingly demonstrate the viability of our method, which opens up possibilities to operate DNNs in mission-critical applications. For example, using our method an unprecedented 2% error in top-5 ImageNet classification can be guaranteed with probability 99.9%, and almost 60% test coverage.

The Prediction Advantage: A Universally Meaningful Performance Measure for Classification and Regression

We introduce the Prediction Advantage (PA), a novel performance measure for prediction functions under any loss function (e.g., classification or regression). The PA is defined as the performance advantage relative to the Bayesian risk restricted to knowing only the distribution of the labels. We derive the PA for well-known loss functions, including 0/1 loss, cross-entropy loss, absolute loss, and squared loss. In the latter case, the PA is identical to the well-known R-squared measure, widely used in statistics. The use of the PA ensures meaningful quantification of prediction performance, which is not guaranteed, for example, when dealing with noisy imbalanced classification problems. We argue that among several known alternative performance measures, PA is the best (and only) quantity ensuring meaningfulness for all noise and imbalance levels.