The Prediction Advantage: A Universally Meaningful Performance Measure for Classification and Regression
Paper and Code
May 26, 2017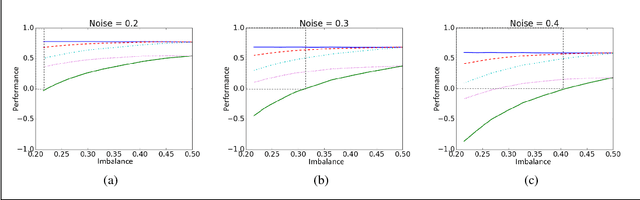
We introduce the Prediction Advantage (PA), a novel performance measure for prediction functions under any loss function (e.g., classification or regression). The PA is defined as the performance advantage relative to the Bayesian risk restricted to knowing only the distribution of the labels. We derive the PA for well-known loss functions, including 0/1 loss, cross-entropy loss, absolute loss, and squared loss. In the latter case, the PA is identical to the well-known R-squared measure, widely used in statistics. The use of the PA ensures meaningful quantification of prediction performance, which is not guaranteed, for example, when dealing with noisy imbalanced classification problems. We argue that among several known alternative performance measures, PA is the best (and only) quantity ensuring meaningfulness for all noise and imbalance levels.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge