The Prediction Advantage: A Universally Meaningful Performance Measure for Classification and Regression

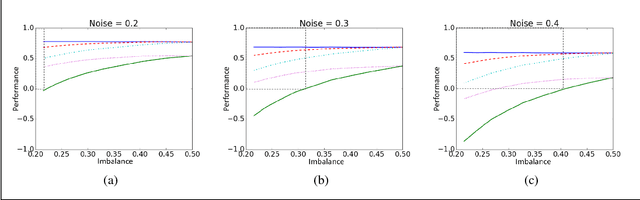
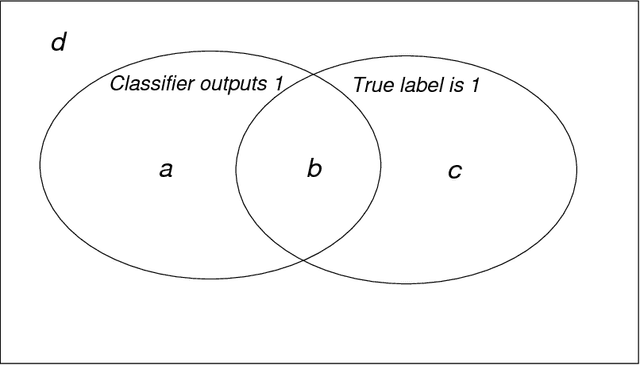
We introduce the Prediction Advantage (PA), a novel performance measure for prediction functions under any loss function (e.g., classification or regression). The PA is defined as the performance advantage relative to the Bayesian risk restricted to knowing only the distribution of the labels. We derive the PA for well-known loss functions, including 0/1 loss, cross-entropy loss, absolute loss, and squared loss. In the latter case, the PA is identical to the well-known R-squared measure, widely used in statistics. The use of the PA ensures meaningful quantification of prediction performance, which is not guaranteed, for example, when dealing with noisy imbalanced classification problems. We argue that among several known alternative performance measures, PA is the best (and only) quantity ensuring meaningfulness for all noise and imbalance levels.

A Compression Technique for Analyzing Disagreement-Based Active Learning

We introduce a new and improved characterization of the label complexity of disagreement-based active learning, in which the leading quantity is the version space compression set size. This quantity is defined as the size of the smallest subset of the training data that induces the same version space. We show various applications of the new characterization, including a tight analysis of CAL and refined label complexity bounds for linear separators under mixtures of Gaussians and axis-aligned rectangles under product densities. The version space compression set size, as well as the new characterization of the label complexity, can be naturally extended to agnostic learning problems, for which we show new speedup results for two well known active learning algorithms.