NVIDIA Nemotron 3: Efficient and Open Intelligence

We introduce the Nemotron 3 family of models - Nano, Super, and Ultra. These models deliver strong agentic, reasoning, and conversational capabilities. The Nemotron 3 family uses a Mixture-of-Experts hybrid Mamba-Transformer architecture to provide best-in-class throughput and context lengths of up to 1M tokens. Super and Ultra models are trained with NVFP4 and incorporate LatentMoE, a novel approach that improves model quality. The two larger models also include MTP layers for faster text generation. All Nemotron 3 models are post-trained using multi-environment reinforcement learning enabling reasoning, multi-step tool use, and support granular reasoning budget control. Nano, the smallest model, outperforms comparable models in accuracy while remaining extremely cost-efficient for inference. Super is optimized for collaborative agents and high-volume workloads such as IT ticket automation. Ultra, the largest model, provides state-of-the-art accuracy and reasoning performance. Nano is released together with its technical report and this white paper, while Super and Ultra will follow in the coming months. We will openly release the model weights, pre- and post-training software, recipes, and all data for which we hold redistribution rights.

Changing Base Without Losing Pace: A GPU-Efficient Alternative to MatMul in DNNs

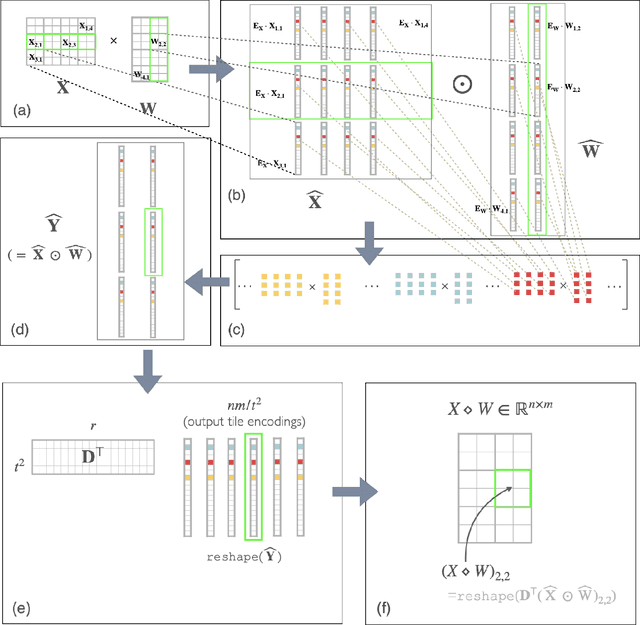
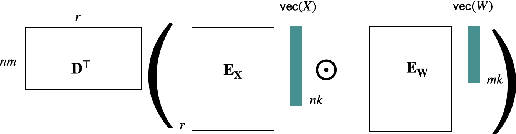
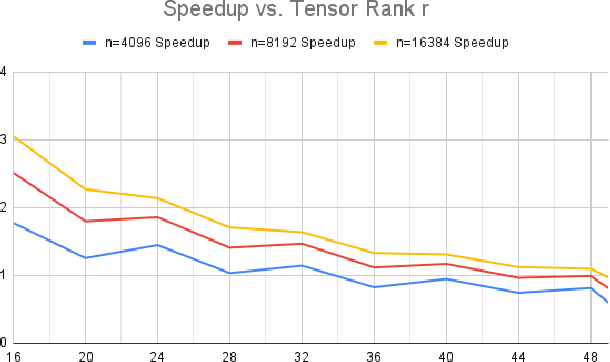
We propose a cheaper alternative bilinear operator to matrix-multiplication in deep neural networks (DNNs). Unlike many stubborn attempts to accelerate MatMuls in DNN inference, this operator is supported by capabilities of existing GPU hardware, most notably NVIDIA TensorCores. To our knowledge, this is the first GPU-native acceleration technique which \emph{does not decrease} (in fact, increases) the number of trainable parameters of the network, mitigating the accuracy-loss of compression-based techniques. Hence, this operator is at the same time more expressive than MatMul, yet requires substantially \emph{fewer} FLOPs to evaluate. We term this new operator \emph{Strassen-Tile} (STL). The main idea behind STL$(X,W)$ is a \emph{local} change-of-basis (learnable encoder) on weights and activation \emph{tiles}, after which we perform batched \emph{elementwise} products between tiles, and a final decoding transformation (inspired by algebraic pipelines from fast matrix and polynomial multiplication). We compare STL against two benchmarks. The first one is SoTA T2T-ViT on Imagenet-1K. Here we show that replacing \emph{all} linear layers with STL and training from scratch, results in factor x2.7 reduction in FLOPs with a 0.5 \emph{accuracy improvement}. Our second speed-accuracy comparison benchmark for pretrained LLMs is the most practical GPU-acceleration technique, \twofour structured Sparsity. Finetuning TinyLlama \cite{tinyllama24} with STL layers on the Slim Pajama dataset, achieves similar accuracy to 2:4, with x2.2 FLOP speedup compared to x1.7 of the latter. Finally, we discuss a group-theoretic approach for discovering \emph{universal} encoders for STL, which could lead to fast \emph{black-box} acceleration via approximate matrix-multiplication (AMM).

Puzzle: Distillation-Based NAS for Inference-Optimized LLMs

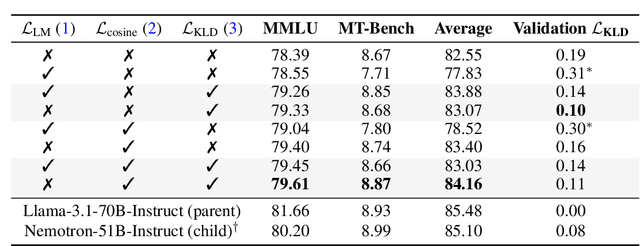
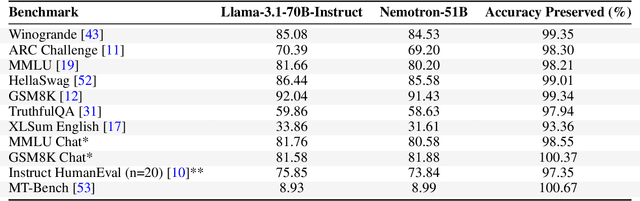
Large language models (LLMs) have demonstrated remarkable capabilities, but their adoption is limited by high computational costs during inference. While increasing parameter counts enhances accuracy, it also widens the gap between state-of-the-art capabilities and practical deployability. We present Puzzle, a framework to accelerate LLM inference on specific hardware while preserving their capabilities. Through an innovative application of neural architecture search (NAS) at an unprecedented scale, Puzzle systematically optimizes models with tens of billions of parameters under hardware constraints. Our approach utilizes blockwise local knowledge distillation (BLD) for parallel architecture exploration and employs mixed-integer programming for precise constraint optimization. We demonstrate the real-world impact of our framework through Llama-3.1-Nemotron-51B-Instruct (Nemotron-51B), a publicly available model derived from Llama-3.1-70B-Instruct. Nemotron-51B achieves a 2.17x inference throughput speedup, fitting on a single NVIDIA H100 GPU while preserving 98.4% of the original model's capabilities. Nemotron-51B currently stands as the most accurate language model capable of inference on a single GPU with large batch sizes. Remarkably, this transformation required just 45B training tokens, compared to over 15T tokens used for the 70B model it was derived from. This establishes a new paradigm where powerful models can be optimized for efficient deployment with only negligible compromise of their capabilities, demonstrating that inference performance, not parameter count alone, should guide model selection. With the release of Nemotron-51B and the presentation of the Puzzle framework, we provide practitioners immediate access to state-of-the-art language modeling capabilities at significantly reduced computational costs.

Efficient NTK using Dimensionality Reduction

Recently, neural tangent kernel (NTK) has been used to explain the dynamics of learning parameters of neural networks, at the large width limit. Quantitative analyses of NTK give rise to network widths that are often impractical and incur high costs in time and energy in both training and deployment. Using a matrix factorization technique, we show how to obtain similar guarantees to those obtained by a prior analysis while reducing training and inference resource costs. The importance of our result further increases when the input points' data dimension is in the same order as the number of input points. More generally, our work suggests how to analyze large width networks in which dense linear layers are replaced with a low complexity factorization, thus reducing the heavy dependence on the large width.

Sparse Linear Networks with a Fixed Butterfly Structure: Theory and Practice

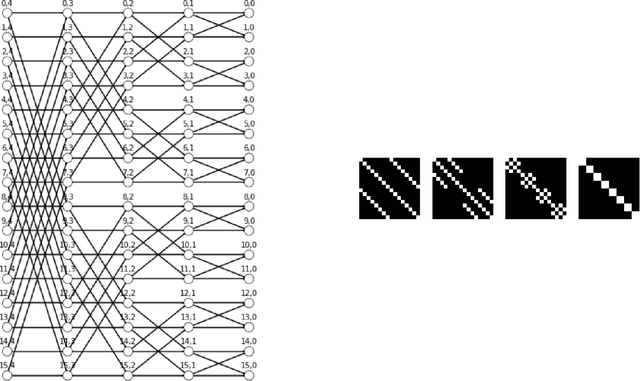
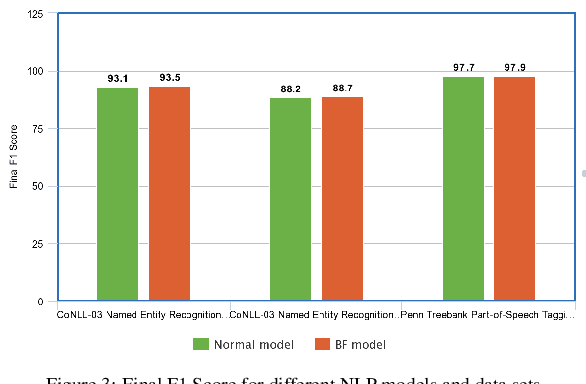
Fast Fourier transform, Wavelets, and other well-known transforms in signal processing have a structured representation as a product of sparse matrices which are referred to as butterfly structures. Research in the recent past have used such structured linear networks along with randomness as pre-conditioners to improve the computational performance of large scale linear algebraic operations. With the advent of deep learning and AI and the computational efficiency of such structured matrices, it is natural to study sparse linear deep networks in which the location of the non-zero weights are predetermined by the butterfly structure. This work studies, both theoretically and empirically, the feasibility of training such networks in different scenarios. Unlike convolutional neural networks, which are structured sparse networks designed to recognize local patterns in lattices representing a spatial or a temporal structure, the butterfly architecture used in this work can replace any dense linear operator with a gadget consisting of a sequence of logarithmically (in the network width) many sparse layers, containing a total of near linear number of weights. This improves on the quadratic number of weights required in a standard dense layer, with little compromise in expressibility of the resulting operator. We show in a collection of empirical experiments that our proposed architecture not only produces results that match and often outperform existing known architectures, but it also offers faster training and prediction in deployment. This empirical phenomenon is observed in a wide variety of experiments that we report, including both supervised prediction on NLP and vision data, as well as in unsupervised representation learning using autoencoders. Preliminary theoretical results presented in the paper explain why training speed and outcome are not compromised by our proposed approach.

Spatial contrasting for deep unsupervised learning

Convolutional networks have marked their place over the last few years as the best performing model for various visual tasks. They are, however, most suited for supervised learning from large amounts of labeled data. Previous attempts have been made to use unlabeled data to improve model performance by applying unsupervised techniques. These attempts require different architectures and training methods. In this work we present a novel approach for unsupervised training of Convolutional networks that is based on contrasting between spatial regions within images. This criterion can be employed within conventional neural networks and trained using standard techniques such as SGD and back-propagation, thus complementing supervised methods.

Semi-supervised deep learning by metric embedding

Deep networks are successfully used as classification models yielding state-of-the-art results when trained on a large number of labeled samples. These models, however, are usually much less suited for semi-supervised problems because of their tendency to overfit easily when trained on small amounts of data. In this work we will explore a new training objective that is targeting a semi-supervised regime with only a small subset of labeled data. This criterion is based on a deep metric embedding over distance relations within the set of labeled samples, together with constraints over the embeddings of the unlabeled set. The final learned representations are discriminative in euclidean space, and hence can be used with subsequent nearest-neighbor classification using the labeled samples.

Deep unsupervised learning through spatial contrasting

Convolutional networks have marked their place over the last few years as the best performing model for various visual tasks. They are, however, most suited for supervised learning from large amounts of labeled data. Previous attempts have been made to use unlabeled data to improve model performance by applying unsupervised techniques. These attempts require different architectures and training methods. In this work we present a novel approach for unsupervised training of Convolutional networks that is based on contrasting between spatial regions within images. This criterion can be employed within conventional neural networks and trained using standard techniques such as SGD and back-propagation, thus complementing supervised methods.

Deep metric learning using Triplet network

Deep learning has proven itself as a successful set of models for learning useful semantic representations of data. These, however, are mostly implicitly learned as part of a classification task. In this paper we propose the triplet network model, which aims to learn useful representations by distance comparisons. A similar model was defined by Wang et al. (2014), tailor made for learning a ranking for image information retrieval. Here we demonstrate using various datasets that our model learns a better representation than that of its immediate competitor, the Siamese network. We also discuss future possible usage as a framework for unsupervised learning.

Bandit Online Optimization Over the Permutahedron

The permutahedron is the convex polytope with vertex set consisting of the vectors $(\pi(1),\dots, \pi(n))$ for all permutations (bijections) $\pi$ over $\{1,\dots, n\}$. We study a bandit game in which, at each step $t$, an adversary chooses a hidden weight weight vector $s_t$, a player chooses a vertex $\pi_t$ of the permutahedron and suffers an observed loss of $\sum_{i=1}^n \pi(i) s_t(i)$. A previous algorithm CombBand of Cesa-Bianchi et al (2009) guarantees a regret of $O(n\sqrt{T \log n})$ for a time horizon of $T$. Unfortunately, CombBand requires at each step an $n$-by-$n$ matrix permanent approximation to within improved accuracy as $T$ grows, resulting in a total running time that is super linear in $T$, making it impractical for large time horizons. We provide an algorithm of regret $O(n^{3/2}\sqrt{T})$ with total time complexity $O(n^3T)$. The ideas are a combination of CombBand and a recent algorithm by Ailon (2013) for online optimization over the permutahedron in the full information setting. The technical core is a bound on the variance of the Plackett-Luce noisy sorting process's "pseudo loss". The bound is obtained by establishing positive semi-definiteness of a family of 3-by-3 matrices generated from rational functions of exponentials of 3 parameters.