Supratim Shit
Deterministic Coreset for Lp Subspace
Jan 01, 2026Abstract:We introduce the first iterative algorithm for constructing a $\varepsilon$-coreset that guarantees deterministic $\ell_p$ subspace embedding for any $p \in [1,\infty)$ and any $\varepsilon > 0$. For a given full rank matrix $\mathbf{X} \in \mathbb{R}^{n \times d}$ where $n \gg d$, $\mathbf{X}' \in \mathbb{R}^{m \times d}$ is an $(\varepsilon,\ell_p)$-subspace embedding of $\mathbf{X}$, if for every $\mathbf{q} \in \mathbb{R}^d$, $(1-\varepsilon)\|\mathbf{Xq}\|_{p}^{p} \leq \|\mathbf{X'q}\|_{p}^{p} \leq (1+\varepsilon)\|\mathbf{Xq}\|_{p}^{p}$. Specifically, in this paper, $\mathbf{X}'$ is a weighted subset of rows of $\mathbf{X}$ which is commonly known in the literature as a coreset. In every iteration, the algorithm ensures that the loss on the maintained set is upper and lower bounded by the loss on the original dataset with appropriate scalings. So, unlike typical coreset guarantees, due to bounded loss, our coreset gives a deterministic guarantee for the $\ell_p$ subspace embedding. For an error parameter $\varepsilon$, our algorithm takes $O(\mathrm{poly}(n,d,\varepsilon^{-1}))$ time and returns a deterministic $\varepsilon$-coreset, for $\ell_p$ subspace embedding whose size is $O\left(\frac{d^{\max\{1,p/2\}}}{\varepsilon^{2}}\right)$. Here, we remove the $\log$ factors in the coreset size, which had been a long-standing open problem. Our coresets are optimal as they are tight with the lower bound. As an application, our coreset can also be used for approximately solving the $\ell_p$ regression problem in a deterministic manner.
Accurate Coresets for Latent Variable Models and Regularized Regression
Dec 28, 2024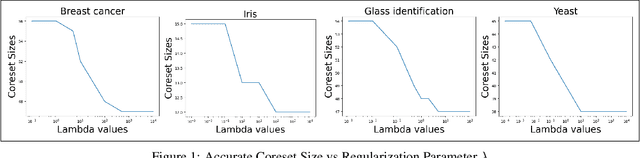


Abstract:Accurate coresets are a weighted subset of the original dataset, ensuring a model trained on the accurate coreset maintains the same level of accuracy as a model trained on the full dataset. Primarily, these coresets have been studied for a limited range of machine learning models. In this paper, we introduce a unified framework for constructing accurate coresets. Using this framework, we present accurate coreset construction algorithms for general problems, including a wide range of latent variable model problems and $\ell_p$-regularized $\ell_p$-regression. For latent variable models, our coreset size is $O\left(\mathrm{poly}(k)\right)$, where $k$ is the number of latent variables. For $\ell_p$-regularized $\ell_p$-regression, our algorithm captures the reduction of model complexity due to regularization, resulting in a coreset whose size is always smaller than $d^{p}$ for a regularization parameter $\lambda > 0$. Here, $d$ is the dimension of the input points. This inherently improves the size of the accurate coreset for ridge regression. We substantiate our theoretical findings with extensive experimental evaluations on real datasets.
Efficient NTK using Dimensionality Reduction
Oct 10, 2022Abstract:Recently, neural tangent kernel (NTK) has been used to explain the dynamics of learning parameters of neural networks, at the large width limit. Quantitative analyses of NTK give rise to network widths that are often impractical and incur high costs in time and energy in both training and deployment. Using a matrix factorization technique, we show how to obtain similar guarantees to those obtained by a prior analysis while reducing training and inference resource costs. The importance of our result further increases when the input points' data dimension is in the same order as the number of input points. More generally, our work suggests how to analyze large width networks in which dense linear layers are replaced with a low complexity factorization, thus reducing the heavy dependence on the large width.
Online Coresets for Clustering with Bregman Divergences
Dec 11, 2020
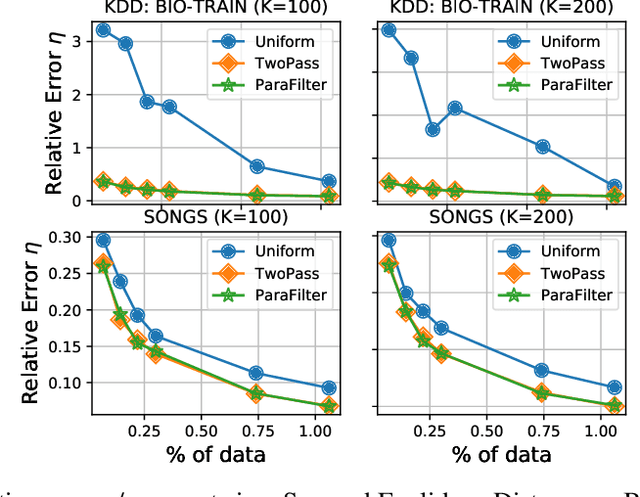
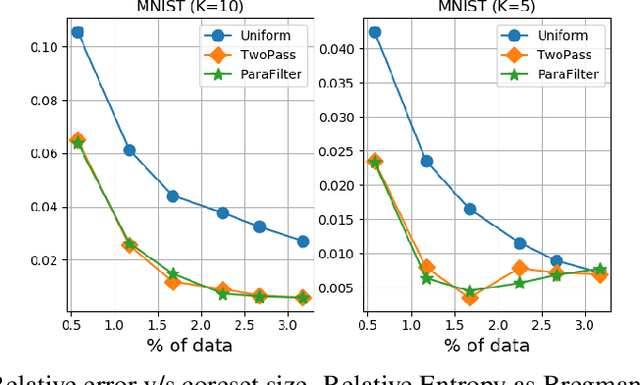
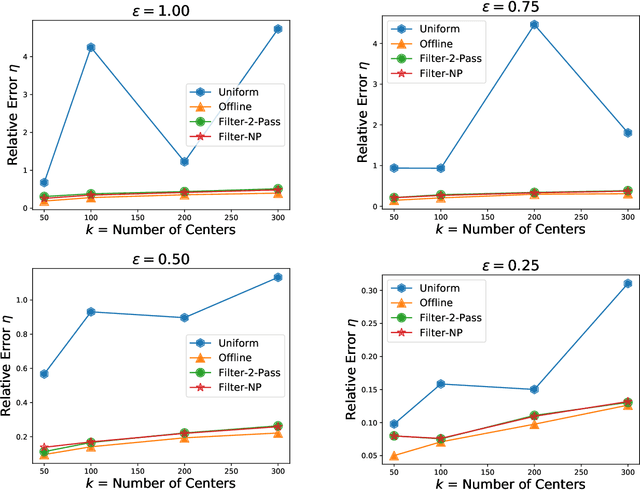
Abstract:We present algorithms that create coresets in an online setting for clustering problems according to a wide subset of Bregman divergences. Notably, our coresets have a small additive error, similar in magnitude to the lightweight coresets Bachem et. al. 2018, and take update time $O(d)$ for every incoming point where $d$ is dimension of the point. Our first algorithm gives online coresets of size $\tilde{O}(\mbox{poly}(k,d,\epsilon,\mu))$ for $k$-clusterings according to any $\mu$-similar Bregman divergence. We further extend this algorithm to show existence of a non-parametric coresets, where the coreset size is independent of $k$, the number of clusters, for the same subclass of Bregman divergences. Our non-parametric coresets are larger by a factor of $O(\log n)$ ($n$ is number of points) and have similar (small) additive guarantee. At the same time our coresets also function as lightweight coresets for non-parametric versions of the Bregman clustering like DP-Means. While these coresets provide additive error guarantees, they are also significantly smaller (scaling with $O(\log n)$ as opposed to $O(d^d)$ for points in $\~R^d$) than the (relative-error) coresets obtained in Bachem et. al. 2015 for DP-Means. While our non-parametric coresets are existential, we give an algorithmic version under certain assumptions.
On Coresets For Regularized Regression
Jun 30, 2020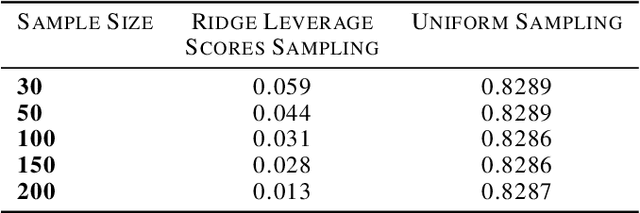
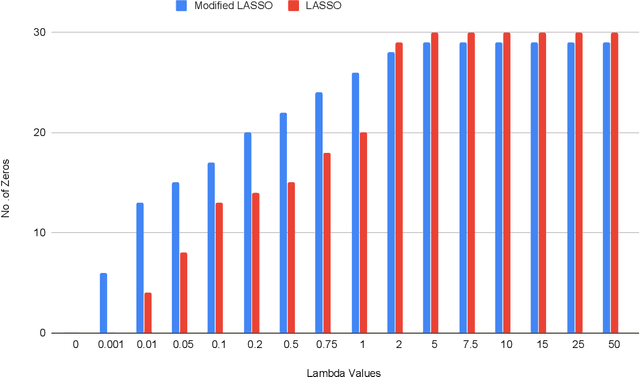
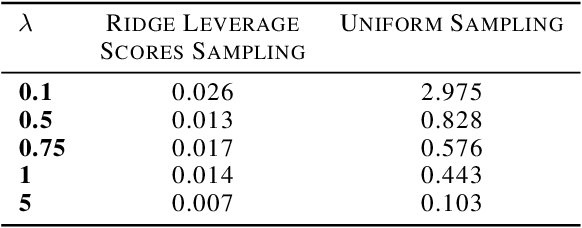
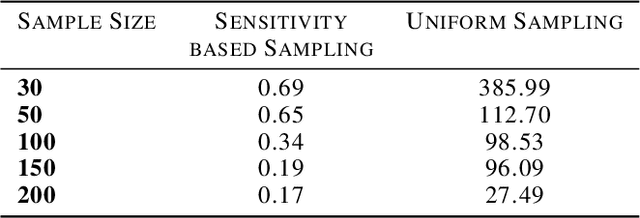
Abstract:We study the effect of norm based regularization on the size of coresets for regression problems. Specifically, given a matrix $ \mathbf{A} \in {\mathbb{R}}^{n \times d}$ with $n\gg d$ and a vector $\mathbf{b} \in \mathbb{R} ^ n $ and $\lambda > 0$, we analyze the size of coresets for regularized versions of regression of the form $\|\mathbf{Ax}-\mathbf{b}\|_p^r + \lambda\|{\mathbf{x}}\|_q^s$ . Prior work has shown that for ridge regression (where $p,q,r,s=2$) we can obtain a coreset that is smaller than the coreset for the unregularized counterpart i.e. least squares regression (Avron et al). We show that when $r \neq s$, no coreset for regularized regression can have size smaller than the optimal coreset of the unregularized version. The well known lasso problem falls under this category and hence does not allow a coreset smaller than the one for least squares regression. We propose a modified version of the lasso problem and obtain for it a coreset of size smaller than the least square regression. We empirically show that the modified version of lasso also induces sparsity in solution, similar to the original lasso. We also obtain smaller coresets for $\ell_p$ regression with $\ell_p$ regularization. We extend our methods to multi response regularized regression. Finally, we empirically demonstrate the coreset performance for the modified lasso and the $\ell_1$ regression with $\ell_1$ regularization.
Streaming Coresets for Symmetric Tensor Factorization
Jun 01, 2020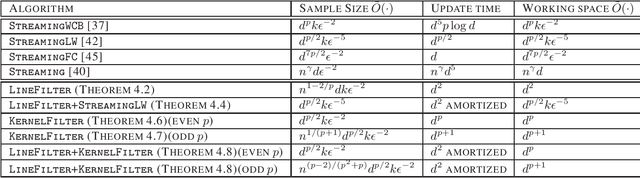
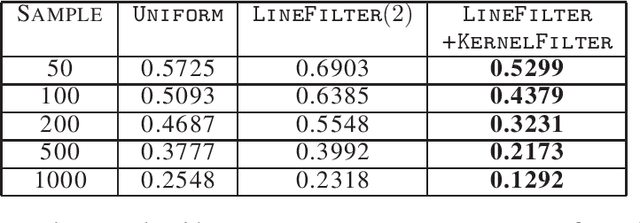
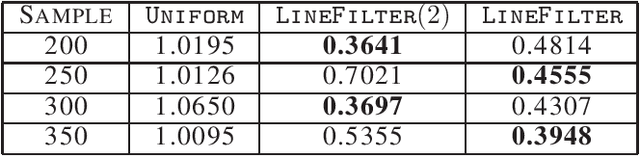
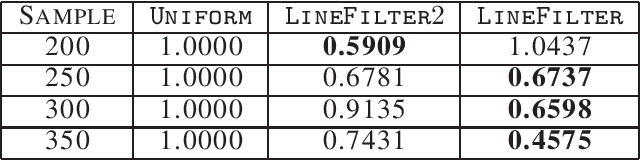
Abstract:Factorizing tensors has recently become an important optimization module in a number of machine learning pipelines, especially in latent variable models. We show how to do this efficiently in the streaming setting. Given a set of $n$ vectors, each in $\mathbb{R}^d$, we present algorithms to select a sublinear number of these vectors as coreset, while guaranteeing that the CP decomposition of the $p$-moment tensor of the coreset approximates the corresponding decomposition of the $p$-moment tensor computed from the full data. We introduce two novel algorithmic techniques: online filtering and kernelization. Using these two, we present four algorithms that achieve different tradeoffs of coreset size, update time and working space, beating or matching various state of the art algorithms. In case of matrices (2-ordered tensor) our online row sampling algorithm guarantees $(1 \pm \epsilon)$ relative error spectral approximation. We show applications of our algorithms in learning single topic modeling.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge