Jayesh Choudhari
Online Coresets for Clustering with Bregman Divergences
Dec 11, 2020
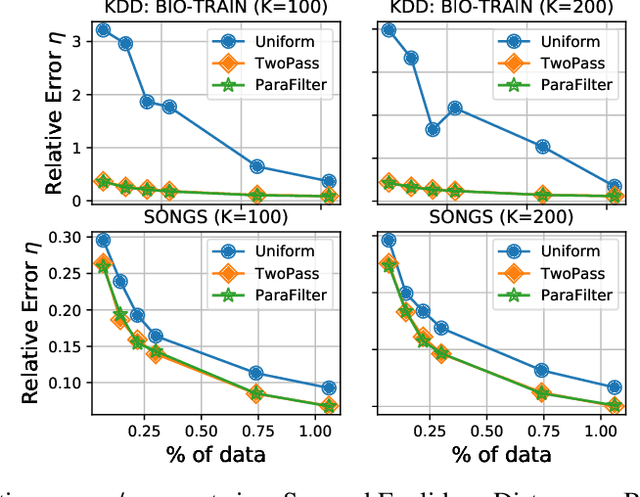
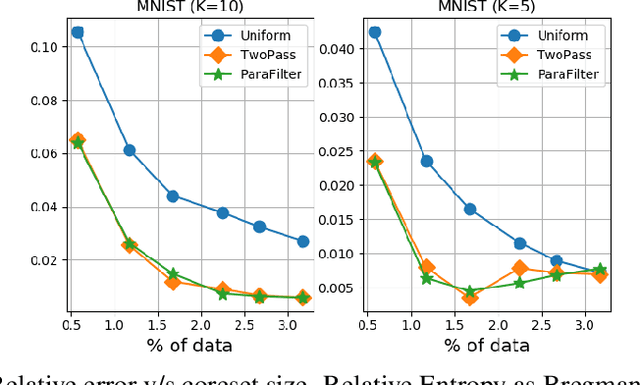
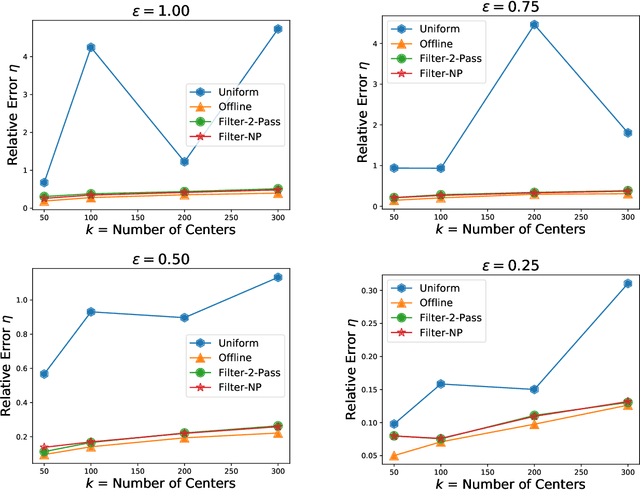
Abstract:We present algorithms that create coresets in an online setting for clustering problems according to a wide subset of Bregman divergences. Notably, our coresets have a small additive error, similar in magnitude to the lightweight coresets Bachem et. al. 2018, and take update time $O(d)$ for every incoming point where $d$ is dimension of the point. Our first algorithm gives online coresets of size $\tilde{O}(\mbox{poly}(k,d,\epsilon,\mu))$ for $k$-clusterings according to any $\mu$-similar Bregman divergence. We further extend this algorithm to show existence of a non-parametric coresets, where the coreset size is independent of $k$, the number of clusters, for the same subclass of Bregman divergences. Our non-parametric coresets are larger by a factor of $O(\log n)$ ($n$ is number of points) and have similar (small) additive guarantee. At the same time our coresets also function as lightweight coresets for non-parametric versions of the Bregman clustering like DP-Means. While these coresets provide additive error guarantees, they are also significantly smaller (scaling with $O(\log n)$ as opposed to $O(d^d)$ for points in $\~R^d$) than the (relative-error) coresets obtained in Bachem et. al. 2015 for DP-Means. While our non-parametric coresets are existential, we give an algorithmic version under certain assumptions.
Streaming Coresets for Symmetric Tensor Factorization
Jun 01, 2020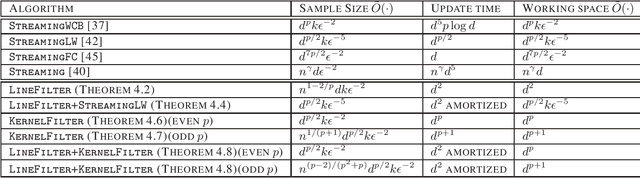
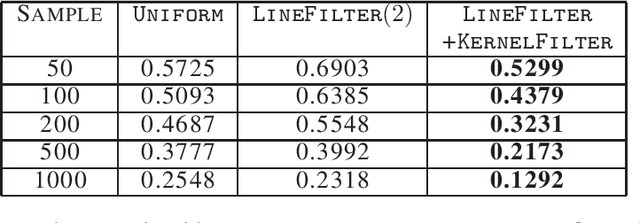
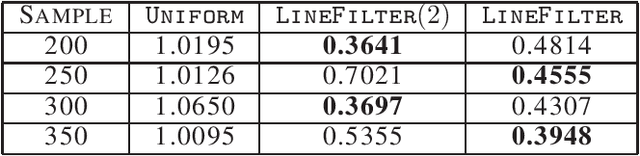
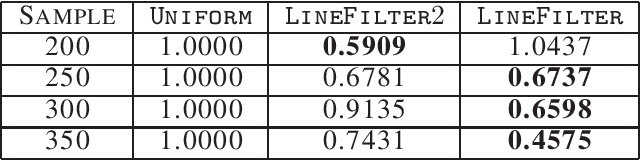
Abstract:Factorizing tensors has recently become an important optimization module in a number of machine learning pipelines, especially in latent variable models. We show how to do this efficiently in the streaming setting. Given a set of $n$ vectors, each in $\mathbb{R}^d$, we present algorithms to select a sublinear number of these vectors as coreset, while guaranteeing that the CP decomposition of the $p$-moment tensor of the coreset approximates the corresponding decomposition of the $p$-moment tensor computed from the full data. We introduce two novel algorithmic techniques: online filtering and kernelization. Using these two, we present four algorithms that achieve different tradeoffs of coreset size, update time and working space, beating or matching various state of the art algorithms. In case of matrices (2-ordered tensor) our online row sampling algorithm guarantees $(1 \pm \epsilon)$ relative error spectral approximation. We show applications of our algorithms in learning single topic modeling.
Discovering Topical Interactions in Text-based Cascades using Hidden Markov Hawkes Processes
Sep 12, 2018


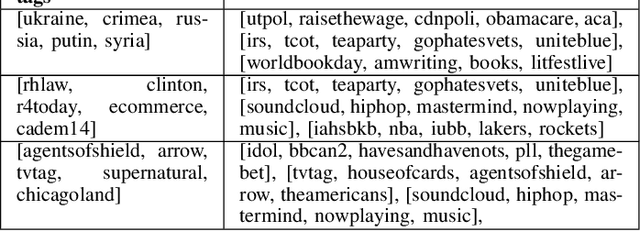
Abstract:Social media conversations unfold based on complex interactions between users, topics and time. While recent models have been proposed to capture network strengths between users, users' topical preferences and temporal patterns between posting and response times, interaction patterns between topics has not been studied. We propose the Hidden Markov Hawkes Process (HMHP) that incorporates topical Markov Chains within Hawkes processes to jointly model topical interactions along with user-user and user-topic patterns. We propose a Gibbs sampling algorithm for HMHP that jointly infers the network strengths, diffusion paths, the topics of the posts as well as the topic-topic interactions. We show using experiments on real and semi-synthetic data that HMHP is able to generalize better and recover the network strengths, topics and diffusion paths more accurately than state-of-the-art baselines. More interestingly, HMHP finds insightful interactions between topics in real tweets which no existing model is able to do.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge