Deterministic Coreset for Lp Subspace

We introduce the first iterative algorithm for constructing a $\varepsilon$-coreset that guarantees deterministic $\ell_p$ subspace embedding for any $p \in [1,\infty)$ and any $\varepsilon > 0$. For a given full rank matrix $\mathbf{X} \in \mathbb{R}^{n \times d}$ where $n \gg d$, $\mathbf{X}' \in \mathbb{R}^{m \times d}$ is an $(\varepsilon,\ell_p)$-subspace embedding of $\mathbf{X}$, if for every $\mathbf{q} \in \mathbb{R}^d$, $(1-\varepsilon)\|\mathbf{Xq}\|_{p}^{p} \leq \|\mathbf{X'q}\|_{p}^{p} \leq (1+\varepsilon)\|\mathbf{Xq}\|_{p}^{p}$. Specifically, in this paper, $\mathbf{X}'$ is a weighted subset of rows of $\mathbf{X}$ which is commonly known in the literature as a coreset. In every iteration, the algorithm ensures that the loss on the maintained set is upper and lower bounded by the loss on the original dataset with appropriate scalings. So, unlike typical coreset guarantees, due to bounded loss, our coreset gives a deterministic guarantee for the $\ell_p$ subspace embedding. For an error parameter $\varepsilon$, our algorithm takes $O(\mathrm{poly}(n,d,\varepsilon^{-1}))$ time and returns a deterministic $\varepsilon$-coreset, for $\ell_p$ subspace embedding whose size is $O\left(\frac{d^{\max\{1,p/2\}}}{\varepsilon^{2}}\right)$. Here, we remove the $\log$ factors in the coreset size, which had been a long-standing open problem. Our coresets are optimal as they are tight with the lower bound. As an application, our coreset can also be used for approximately solving the $\ell_p$ regression problem in a deterministic manner.

Private Sketches for Linear Regression

Linear regression is frequently applied in a variety of domains. In order to improve the efficiency of these methods, various methods have been developed that compute summaries or \emph{sketches} of the datasets. Certain domains, however, contain sensitive data which necessitates that the application of these statistical methods does not reveal private information. Differentially private (DP) linear regression methods have been developed for mitigating this problem. These techniques typically involve estimating a noisy version of the parameter vector. Instead, we propose releasing private sketches of the datasets. We present differentially private sketches for the problems of least squares regression, as well as least absolute deviations regression. The availability of these private sketches facilitates the application of commonly available solvers for regression, without the risk of privacy leakage.

Linear Programming based Approximation to Individually Fair k-Clustering with Outliers

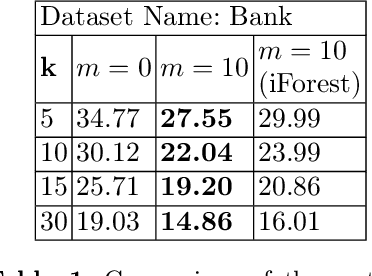
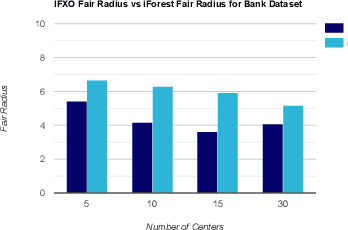
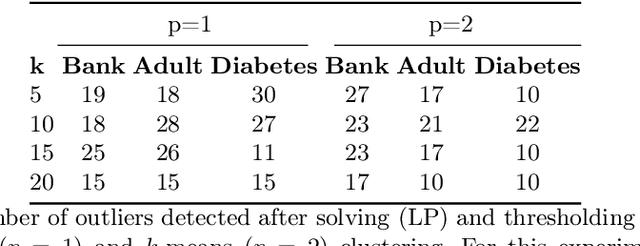
Individual fairness guarantees are often desirable properties to have, but they become hard to formalize when the dataset contains outliers. Here, we investigate the problem of developing an individually fair $k$-means clustering algorithm for datasets that contain outliers. That is, given $n$ points and $k$ centers, we want that for each point which is not an outlier, there must be a center within the $\frac{n}{k}$ nearest neighbours of the given point. While a few of the recent works have looked into individually fair clustering, this is the first work that explores this problem in the presence of outliers for $k$-means clustering. For this purpose, we define and solve a linear program (LP) that helps us identify the outliers. We exclude these outliers from the dataset and apply a rounding algorithm that computes the $k$ centers, such that the fairness constraint of the remaining points is satisfied. We also provide theoretical guarantees that our method leads to a guaranteed approximation of the fair radius as well as the clustering cost. We also demonstrate our techniques empirically on real-world datasets.

Faster Inference Time for GNNs using coarsening

Graph Neural Networks (GNNs) have shown remarkable success in various graph-based tasks, including node classification, node regression, graph classification, and graph regression. However, their scalability remains a significant challenge, particularly when dealing with large-scale graphs. To tackle this challenge, coarsening-based methods are used to reduce the graph into a smaller one, resulting in faster computation. However, no previous research has tackled the computation cost during the inference. This motivated us to ponder whether we can trade off the improvement in training time of coarsening-based approaches with inference time. This paper presents a novel approach to improve the scalability of GNNs through subgraph-based techniques. We reduce the computational burden during the training and inference phases by using the coarsening algorithm to partition large graphs into smaller, manageable subgraphs. Previously, graph-level tasks had not been explored using this approach. We propose a novel approach for using the coarsening algorithm for graph-level tasks such as graph classification and graph regression. We conduct extensive experiments on multiple benchmark datasets to evaluate the performance of our approach. The results demonstrate that our subgraph-based GNN method achieves competitive results in node classification, node regression, graph classification, and graph regression tasks compared to traditional GNN models. Furthermore, our approach significantly reduces the inference time, enabling the practical application of GNNs to large-scale graphs.

Simple Weak Coresets for Non-Decomposable Classification Measures

While coresets have been growing in terms of their application, barring few exceptions, they have mostly been limited to unsupervised settings. We consider supervised classification problems, and non-decomposable evaluation measures in such settings. We show that stratified uniform sampling based coresets have excellent empirical performance that are backed by theoretical guarantees too. We focus on the F1 score and Matthews Correlation Coefficient, two widely used non-decomposable objective functions that are nontrivial to optimize for and show that uniform coresets attain a lower bound for coreset size, and have good empirical performance, comparable with ``smarter'' coreset construction strategies.

A Novel Pipeline for Improving Optical Character Recognition through Post-processing Using Natural Language Processing

Optical Character Recognition (OCR) technology finds applications in digitizing books and unstructured documents, along with applications in other domains such as mobility statistics, law enforcement, traffic, security systems, etc. The state-of-the-art methods work well with the OCR with printed text on license plates, shop names, etc. However, applications such as printed textbooks and handwritten texts have limited accuracy with existing techniques. The reason may be attributed to similar-looking characters and variations in handwritten characters. Since these issues are challenging to address with OCR technologies exclusively, we propose a post-processing approach using Natural Language Processing (NLP) tools. This work presents an end-to-end pipeline that first performs OCR on the handwritten or printed text and then improves its accuracy using NLP.

Improving Expressivity of Graph Neural Networks using Localization

In this paper, we propose localized versions of Weisfeiler-Leman (WL) algorithms in an effort to both increase the expressivity, as well as decrease the computational overhead. We focus on the specific problem of subgraph counting and give localized versions of $k-$WL for any $k$. We analyze the power of Local $k-$WL and prove that it is more expressive than $k-$WL and at most as expressive as $(k+1)-$WL. We give a characterization of patterns whose count as a subgraph and induced subgraph are invariant if two graphs are Local $k-$WL equivalent. We also introduce two variants of $k-$WL: Layer $k-$WL and recursive $k-$WL. These methods are more time and space efficient than applying $k-$WL on the whole graph. We also propose a fragmentation technique that guarantees the exact count of all induced subgraphs of size at most 4 using just $1-$WL. The same idea can be extended further for larger patterns using $k>1$. We also compare the expressive power of Local $k-$WL with other GNN hierarchies and show that given a bound on the time-complexity, our methods are more expressive than the ones mentioned in Papp and Wattenhofer[2022a].

Statistical Measures For Defining Curriculum Scoring Function

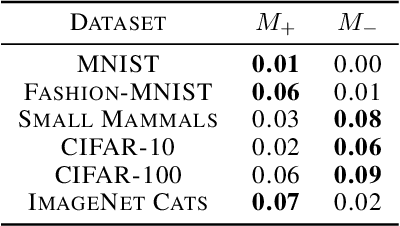
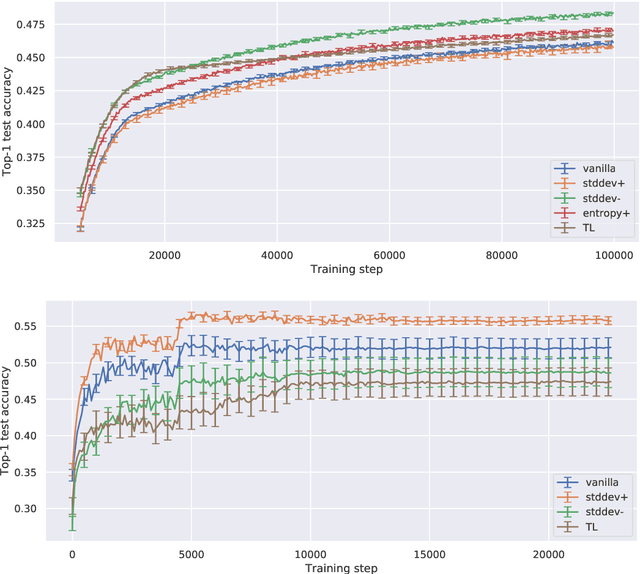
Curriculum learning is a training strategy that sorts the training examples by some measure of their difficulty and gradually exposes them to the learner to improve the network performance. In this work, we propose two novel curriculum learning algorithms, and empirically show their improvements in performance with convolutional and fully-connected neural networks on multiple real image datasets. Motivated by our insights from implicit curriculum ordering, we introduce a simple curriculum learning strategy that uses statistical measures such as standard deviation and entropy values to score the difficulty of data points for real image classification tasks. We also propose and study the performance of a dynamic curriculum learning algorithm. Our dynamic curriculum algorithm tries to reduce the distance between the network weight and an optimal weight at any training step by greedily sampling examples with gradients that are directed towards the optimal weight. Further, we also use our algorithms to discuss why curriculum learning is helpful.

Online Coresets for Clustering with Bregman Divergences

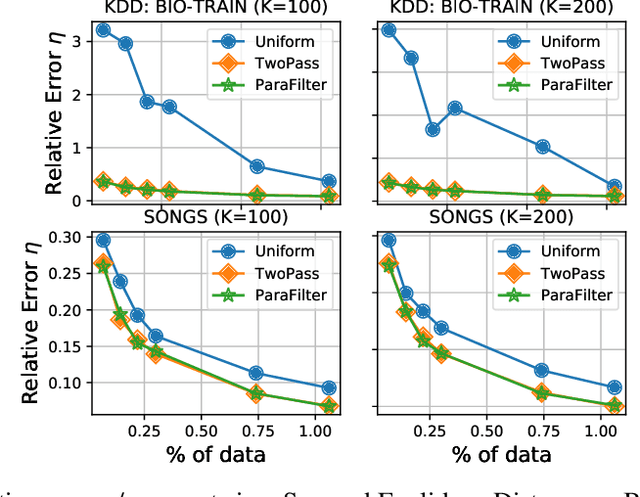
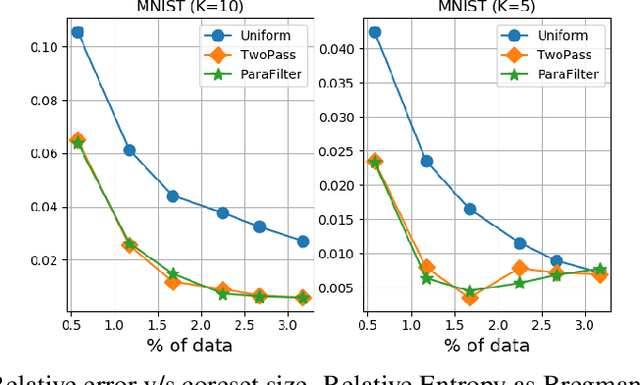
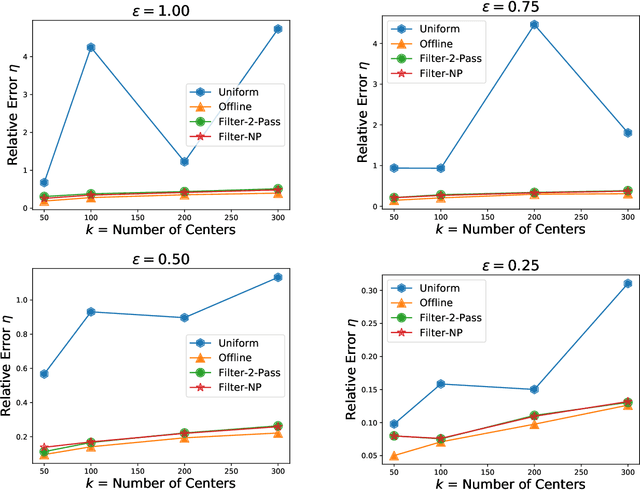
We present algorithms that create coresets in an online setting for clustering problems according to a wide subset of Bregman divergences. Notably, our coresets have a small additive error, similar in magnitude to the lightweight coresets Bachem et. al. 2018, and take update time $O(d)$ for every incoming point where $d$ is dimension of the point. Our first algorithm gives online coresets of size $\tilde{O}(\mbox{poly}(k,d,\epsilon,\mu))$ for $k$-clusterings according to any $\mu$-similar Bregman divergence. We further extend this algorithm to show existence of a non-parametric coresets, where the coreset size is independent of $k$, the number of clusters, for the same subclass of Bregman divergences. Our non-parametric coresets are larger by a factor of $O(\log n)$ ($n$ is number of points) and have similar (small) additive guarantee. At the same time our coresets also function as lightweight coresets for non-parametric versions of the Bregman clustering like DP-Means. While these coresets provide additive error guarantees, they are also significantly smaller (scaling with $O(\log n)$ as opposed to $O(d^d)$ for points in $\~R^d$) than the (relative-error) coresets obtained in Bachem et. al. 2015 for DP-Means. While our non-parametric coresets are existential, we give an algorithmic version under certain assumptions.

On Additive Approximate Submodularity

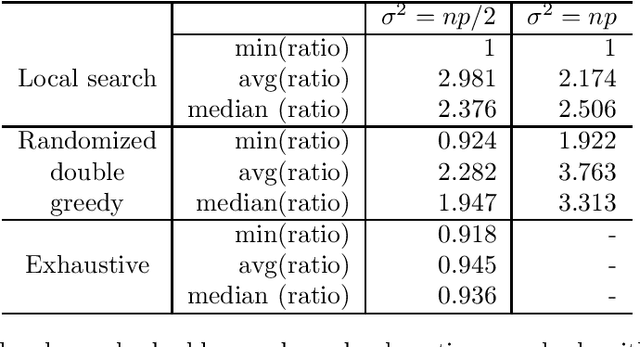
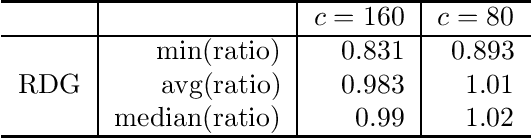
A real-valued set function is (additively) approximately submodular if it satisfies the submodularity conditions with an additive error. Approximate submodularity arises in many settings, especially in machine learning, where the function evaluation might not be exact. In this paper we study how close such approximately submodular functions are to truly submodular functions. We show that an approximately submodular function defined on a ground set of $n$ elements is $O(n^2)$ pointwise-close to a submodular function. This result also provides an algorithmic tool that can be used to adapt existing submodular optimization algorithms to approximately submodular functions. To complement, we show an $\Omega(\sqrt{n})$ lower bound on the distance to submodularity. These results stand in contrast to the case of approximate modularity, where the distance to modularity is a constant, and approximate convexity, where the distance to convexity is logarithmic.