Approximating a RUM from Distributions on k-Slates

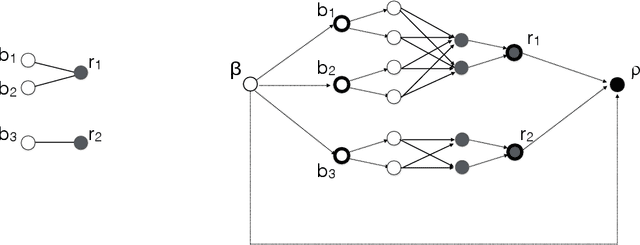
In this work we consider the problem of fitting Random Utility Models (RUMs) to user choices. Given the winner distributions of the subsets of size $k$ of a universe, we obtain a polynomial-time algorithm that finds the RUM that best approximates the given distribution on average. Our algorithm is based on a linear program that we solve using the ellipsoid method. Given that its corresponding separation oracle problem is NP-hard, we devise an approximate separation oracle that can be viewed as a generalization of the weighted feedback arc set problem to hypergraphs. Our theoretical result can also be made practical: we obtain a heuristic that is effective and scales to real-world datasets.

Correlation Clustering Reconstruction in Semi-Adversarial Models

Correlation Clustering is an important clustering problem with many applications. We study the reconstruction version of this problem in which one is seeking to reconstruct a latent clustering that has been corrupted by random noise and adversarial modifications. Concerning the latter, we study a standard "post-adversarial" model, in which adversarial modifications come after the noise, and also introduce and analyze a "pre-adversarial" model in which adversarial modifications come before the noise. Given an input coming from such a semi-adversarial generative model, the goal is to reconstruct almost perfectly and with high probability the latent clustering. We focus on the case where the hidden clusters have equal size and show the following. In the pre-adversarial setting, spectral algorithms are optimal, in the sense that they reconstruct all the way to the information-theoretic threshold beyond which no reconstruction is possible. In contrast, in the post-adversarial setting their ability to restore the hidden clusters stops before the threshold, but the gap is optimally filled by SDP-based algorithms.

On Additive Approximate Submodularity

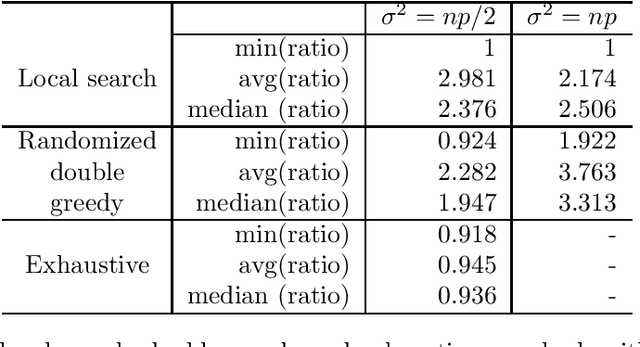
A real-valued set function is (additively) approximately submodular if it satisfies the submodularity conditions with an additive error. Approximate submodularity arises in many settings, especially in machine learning, where the function evaluation might not be exact. In this paper we study how close such approximately submodular functions are to truly submodular functions. We show that an approximately submodular function defined on a ground set of $n$ elements is $O(n^2)$ pointwise-close to a submodular function. This result also provides an algorithmic tool that can be used to adapt existing submodular optimization algorithms to approximately submodular functions. To complement, we show an $\Omega(\sqrt{n})$ lower bound on the distance to submodularity. These results stand in contrast to the case of approximate modularity, where the distance to modularity is a constant, and approximate convexity, where the distance to convexity is logarithmic.

Fair Clustering Through Fairlets

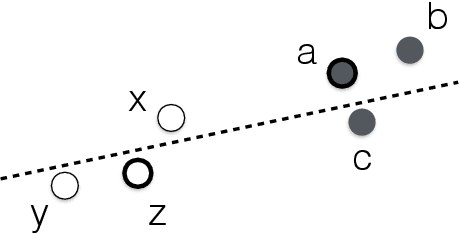
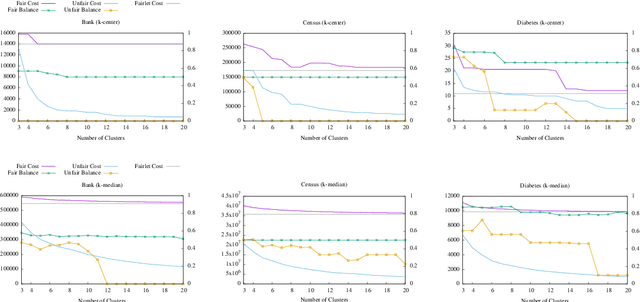
We study the question of fair clustering under the {\em disparate impact} doctrine, where each protected class must have approximately equal representation in every cluster. We formulate the fair clustering problem under both the $k$-center and the $k$-median objectives, and show that even with two protected classes the problem is challenging, as the optimum solution can violate common conventions---for instance a point may no longer be assigned to its nearest cluster center! En route we introduce the concept of fairlets, which are minimal sets that satisfy fair representation while approximately preserving the clustering objective. We show that any fair clustering problem can be decomposed into first finding good fairlets, and then using existing machinery for traditional clustering algorithms. While finding good fairlets can be NP-hard, we proceed to obtain efficient approximation algorithms based on minimum cost flow. We empirically quantify the value of fair clustering on real-world datasets with sensitive attributes.