Learning Multinomial Logits in $O(n \log n)$ time

A Multinomial Logit (MNL) model is composed of a finite universe of items $[n]=\{1,..., n\}$, each assigned a positive weight. A query specifies an admissible subset -- called a slate -- and the model chooses one item from that slate with probability proportional to its weight. This query model is also known as the Plackett-Luce model or conditional sampling oracle in the literature. Although MNLs have been studied extensively, a basic computational question remains open: given query access to slates, how efficiently can we learn weights so that, for every slate, the induced choice distribution is within total variation distance $\varepsilon$ of the ground truth? This question is central to MNL learning and has direct implications for modern recommender system interfaces. We provide two algorithms for this task, one with adaptive queries and one with non-adaptive queries. Each algorithm outputs an MNL $M'$ that induces, for each slate $S$, a distribution $M'_S$ on $S$ that is within $\varepsilon$ total variation distance of the true distribution. Our adaptive algorithm makes $O\left(\frac{n}{\varepsilon^{3}}\log n\right)$ queries, while our non-adaptive algorithm makes $O\left(\frac{n^{2}}{\varepsilon^{3}}\log n \log\frac{n}{\varepsilon}\right)$ queries. Both algorithms query only slates of size two and run in time proportional to their query complexity. We complement these upper bounds with lower bounds of $Ω\left(\frac{n}{\varepsilon^{2}}\log n\right)$ for adaptive queries and $Ω\left(\frac{n^{2}}{\varepsilon^{2}}\log n\right)$ for non-adaptive queries, thus proving that our adaptive algorithm is optimal in its dependence on the support size $n$, while the non-adaptive one is tight within a $\log n$ factor.

Approximating a RUM from Distributions on k-Slates

In this work we consider the problem of fitting Random Utility Models (RUMs) to user choices. Given the winner distributions of the subsets of size $k$ of a universe, we obtain a polynomial-time algorithm that finds the RUM that best approximates the given distribution on average. Our algorithm is based on a linear program that we solve using the ellipsoid method. Given that its corresponding separation oracle problem is NP-hard, we devise an approximate separation oracle that can be viewed as a generalization of the weighted feedback arc set problem to hypergraphs. Our theoretical result can also be made practical: we obtain a heuristic that is effective and scales to real-world datasets.

About latent roles in forecasting players in team sports

Forecasting players in sports has grown in popularity due to the potential for a tactical advantage and the applicability of such research to multi-agent interaction systems. Team sports contain a significant social component that influences interactions between teammates and opponents. However, it still needs to be fully exploited. In this work, we hypothesize that each participant has a specific function in each action and that role-based interaction is critical for predicting players' future moves. We create RolFor, a novel end-to-end model for Role-based Forecasting. RolFor uses a new module we developed called Ordering Neural Networks (OrderNN) to permute the order of the players such that each player is assigned to a latent role. The latent role is then modeled with a RoleGCN. Thanks to its graph representation, it provides a fully learnable adjacency matrix that captures the relationships between roles and is subsequently used to forecast the players' future trajectories. Extensive experiments on a challenging NBA basketball dataset back up the importance of roles and justify our goal of modeling them using optimizable models. When an oracle provides roles, the proposed RolFor compares favorably to the current state-of-the-art (it ranks first in terms of ADE and second in terms of FDE errors). However, training the end-to-end RolFor incurs the issues of differentiability of permutation methods, which we experimentally review. Finally, this work restates differentiable ranking as a difficult open problem and its great potential in conjunction with graph-based interaction models. Project is available at: https://www.pinlab.org/aboutlatentroles

Correlation Clustering Reconstruction in Semi-Adversarial Models

Correlation Clustering is an important clustering problem with many applications. We study the reconstruction version of this problem in which one is seeking to reconstruct a latent clustering that has been corrupted by random noise and adversarial modifications. Concerning the latter, we study a standard "post-adversarial" model, in which adversarial modifications come after the noise, and also introduce and analyze a "pre-adversarial" model in which adversarial modifications come before the noise. Given an input coming from such a semi-adversarial generative model, the goal is to reconstruct almost perfectly and with high probability the latent clustering. We focus on the case where the hidden clusters have equal size and show the following. In the pre-adversarial setting, spectral algorithms are optimal, in the sense that they reconstruct all the way to the information-theoretic threshold beyond which no reconstruction is possible. In contrast, in the post-adversarial setting their ability to restore the hidden clusters stops before the threshold, but the gap is optimally filled by SDP-based algorithms.

OLIVAW: Mastering Othello with neither Humans nor a Penny

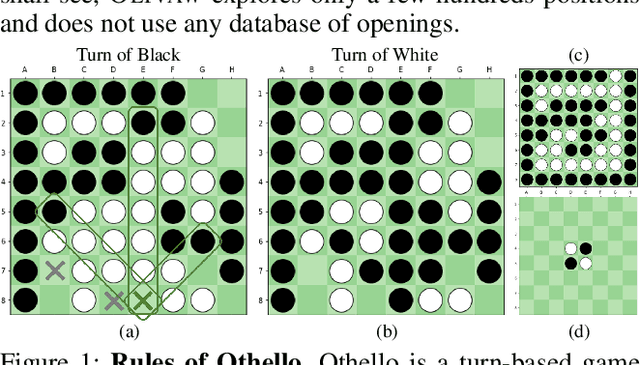
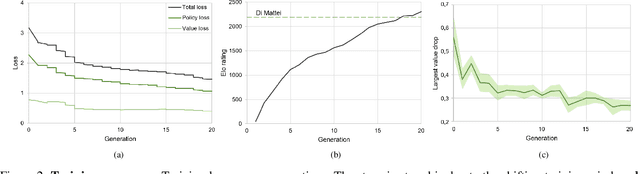
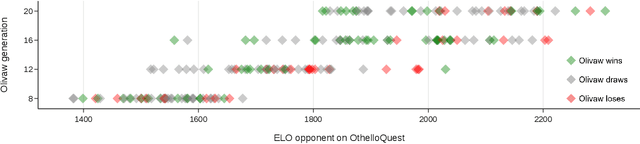
We introduce OLIVAW, an AI Othello player adopting the design principles of the famous AlphaGo series. The main motivation behind OLIVAW was to attain exceptional competence in a non-trivial board game, but at a tiny fraction of the cost of its illustrious predecessors. In this paper we show how OLIVAW successfully met this challenge.