Fair Clustering Through Fairlets
Paper and Code
Feb 15, 2018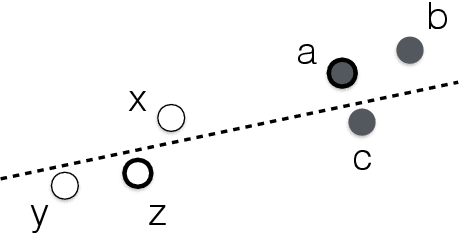
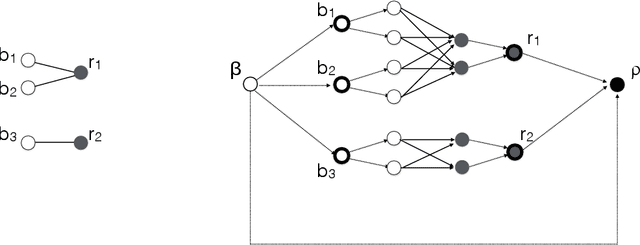
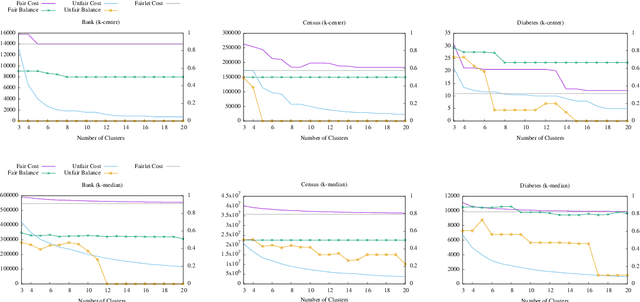
We study the question of fair clustering under the {\em disparate impact} doctrine, where each protected class must have approximately equal representation in every cluster. We formulate the fair clustering problem under both the $k$-center and the $k$-median objectives, and show that even with two protected classes the problem is challenging, as the optimum solution can violate common conventions---for instance a point may no longer be assigned to its nearest cluster center! En route we introduce the concept of fairlets, which are minimal sets that satisfy fair representation while approximately preserving the clustering objective. We show that any fair clustering problem can be decomposed into first finding good fairlets, and then using existing machinery for traditional clustering algorithms. While finding good fairlets can be NP-hard, we proceed to obtain efficient approximation algorithms based on minimum cost flow. We empirically quantify the value of fair clustering on real-world datasets with sensitive attributes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge