Linear Programming based Approximation to Individually Fair k-Clustering with Outliers

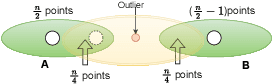
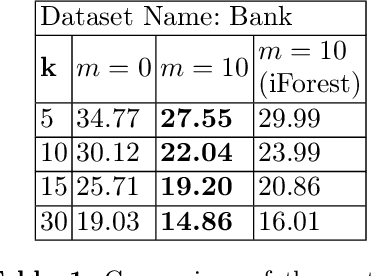
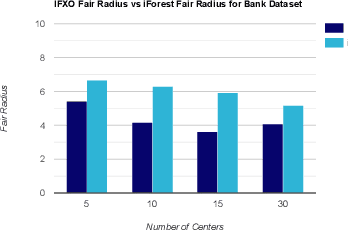
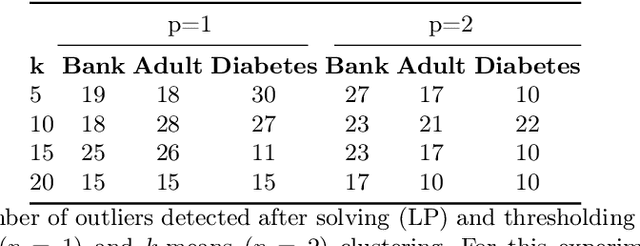
Individual fairness guarantees are often desirable properties to have, but they become hard to formalize when the dataset contains outliers. Here, we investigate the problem of developing an individually fair $k$-means clustering algorithm for datasets that contain outliers. That is, given $n$ points and $k$ centers, we want that for each point which is not an outlier, there must be a center within the $\frac{n}{k}$ nearest neighbours of the given point. While a few of the recent works have looked into individually fair clustering, this is the first work that explores this problem in the presence of outliers for $k$-means clustering. For this purpose, we define and solve a linear program (LP) that helps us identify the outliers. We exclude these outliers from the dataset and apply a rounding algorithm that computes the $k$ centers, such that the fairness constraint of the remaining points is satisfied. We also provide theoretical guarantees that our method leads to a guaranteed approximation of the fair radius as well as the clustering cost. We also demonstrate our techniques empirically on real-world datasets.

Improving Expressivity of Graph Neural Networks using Localization

In this paper, we propose localized versions of Weisfeiler-Leman (WL) algorithms in an effort to both increase the expressivity, as well as decrease the computational overhead. We focus on the specific problem of subgraph counting and give localized versions of $k-$WL for any $k$. We analyze the power of Local $k-$WL and prove that it is more expressive than $k-$WL and at most as expressive as $(k+1)-$WL. We give a characterization of patterns whose count as a subgraph and induced subgraph are invariant if two graphs are Local $k-$WL equivalent. We also introduce two variants of $k-$WL: Layer $k-$WL and recursive $k-$WL. These methods are more time and space efficient than applying $k-$WL on the whole graph. We also propose a fragmentation technique that guarantees the exact count of all induced subgraphs of size at most 4 using just $1-$WL. The same idea can be extended further for larger patterns using $k>1$. We also compare the expressive power of Local $k-$WL with other GNN hierarchies and show that given a bound on the time-complexity, our methods are more expressive than the ones mentioned in Papp and Wattenhofer[2022a].