Vineet Nair
Maximally Useful and Minimally Redundant: The Key to Self Supervised Learning for Imbalanced Data
Sep 10, 2025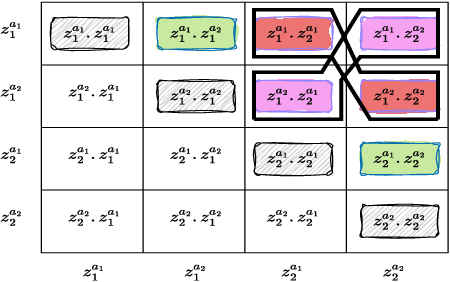
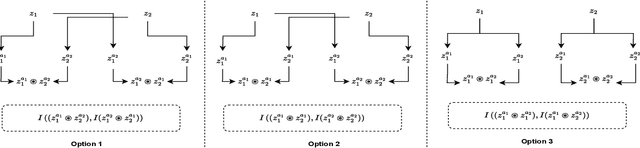

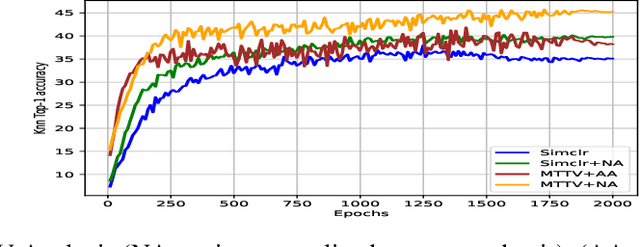
Abstract:The robustness of contrastive self-supervised learning (CSSL) for imbalanced datasets is largely unexplored. CSSL usually makes use of \emph{multi-view} assumptions to learn discriminatory features via similar and dissimilar data samples. CSSL works well on balanced datasets, but does not generalize well for imbalanced datasets. In a very recent paper, as part of future work, Yann LeCun pointed out that the self-supervised multiview framework can be extended to cases involving \emph{more than two views}. Taking a cue from this insight we propose a theoretical justification based on the concept of \emph{mutual information} to support the \emph{more than two views} objective and apply it to the problem of dataset imbalance in self-supervised learning. The proposed method helps extract representative characteristics of the tail classes by segregating between \emph{intra} and \emph{inter} discriminatory characteristics. We introduce a loss function that helps us to learn better representations by filtering out extreme features. Experimental evaluation on a variety of self-supervised frameworks (both contrastive and non-contrastive) also prove that the \emph{more than two view} objective works well for imbalanced datasets. We achieve a new state-of-the-art accuracy in self-supervised imbalanced dataset classification (2\% improvement in Cifar10-LT using Resnet-18, 5\% improvement in Cifar100-LT using Resnet-18, 3\% improvement in Imagenet-LT (1k) using Resnet-50).
Mitigating Disparity while Maximizing Reward: Tight Anytime Guarantee for Improving Bandits
Aug 19, 2022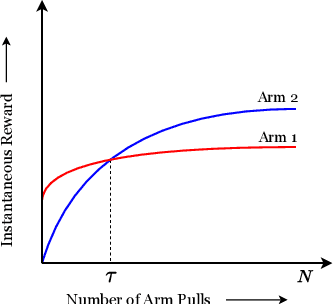
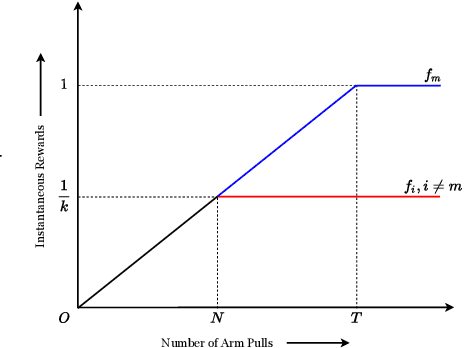
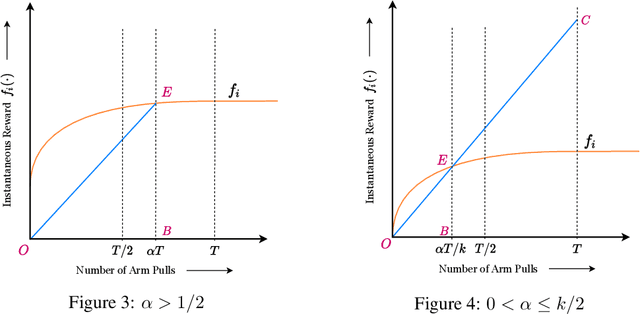
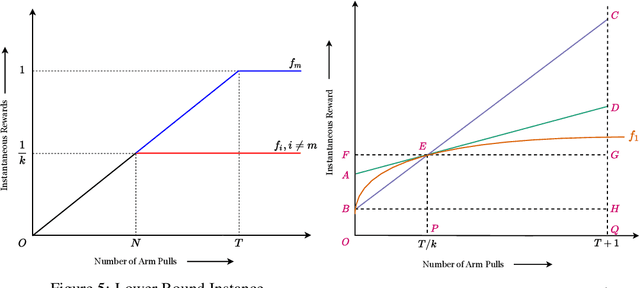
Abstract:We study the Improving Multi-Armed Bandit (IMAB) problem, where the reward obtained from an arm increases with the number of pulls it receives. This model provides an elegant abstraction for many real-world problems in domains such as education and employment, where decisions about the distribution of opportunities can affect the future capabilities of communities and the disparity between them. A decision-maker in such settings must consider the impact of her decisions on future rewards in addition to the standard objective of maximizing her cumulative reward at any time. In many of these applications, the time horizon is unknown to the decision-maker beforehand, which motivates the study of the IMAB problem in the technically more challenging horizon-unaware setting. We study the tension that arises between two seemingly conflicting objectives in the horizon-unaware setting: a) maximizing the cumulative reward at any time based on current rewards of the arms, and b) ensuring that arms with better long-term rewards get sufficient opportunities even if they initially have low rewards. We show that, surprisingly, the two objectives are aligned with each other in this setting. Our main contribution is an anytime algorithm for the IMAB problem that achieves the best possible cumulative reward while ensuring that the arms reach their true potential given sufficient time. Our algorithm mitigates the initial disparity due to lack of opportunity and continues pulling an arm till it stops improving. We prove the optimality of our algorithm by showing that a) any algorithm for the IMAB problem, no matter how utilitarian, must suffer $\Omega(T)$ policy regret and $\Omega(k)$ competitive ratio with respect to the optimal offline policy, and b) the competitive ratio of our algorithm is $O(k)$.
Strategic Representation
Jun 17, 2022
Abstract:Humans have come to rely on machines for reducing excessive information to manageable representations. But this reliance can be abused -- strategic machines might craft representations that manipulate their users. How can a user make good choices based on strategic representations? We formalize this as a learning problem, and pursue algorithms for decision-making that are robust to manipulation. In our main setting of interest, the system represents attributes of an item to the user, who then decides whether or not to consume. We model this interaction through the lens of strategic classification (Hardt et al. 2016), reversed: the user, who learns, plays first; and the system, which responds, plays second. The system must respond with representations that reveal `nothing but the truth' but need not reveal the entire truth. Thus, the user faces the problem of learning set functions under strategic subset selection, which presents distinct algorithmic and statistical challenges. Our main result is a learning algorithm that minimizes error despite strategic representations, and our theoretical analysis sheds light on the trade-off between learning effort and susceptibility to manipulation.
ADVISER: AI-Driven Vaccination Intervention Optimiser for Increasing Vaccine Uptake in Nigeria
Apr 28, 2022

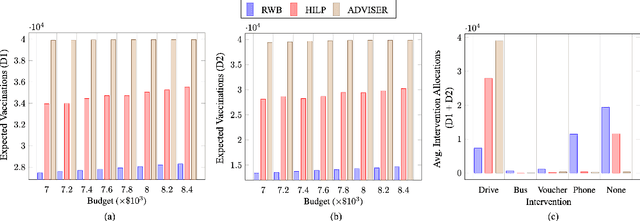
Abstract:More than 5 million children under five years die from largely preventable or treatable medical conditions every year, with an overwhelmingly large proportion of deaths occurring in under-developed countries with low vaccination uptake. One of the United Nations' sustainable development goals (SDG 3) aims to end preventable deaths of newborns and children under five years of age. We focus on Nigeria, where the rate of infant mortality is appalling. We collaborate with HelpMum, a large non-profit organization in Nigeria to design and optimize the allocation of heterogeneous health interventions under uncertainty to increase vaccination uptake, the first such collaboration in Nigeria. Our framework, ADVISER: AI-Driven Vaccination Intervention Optimiser, is based on an integer linear program that seeks to maximize the cumulative probability of successful vaccination. Our optimization formulation is intractable in practice. We present a heuristic approach that enables us to solve the problem for real-world use-cases. We also present theoretical bounds for the heuristic method. Finally, we show that the proposed approach outperforms baseline methods in terms of vaccination uptake through experimental evaluation. HelpMum is currently planning a pilot program based on our approach to be deployed in the largest city of Nigeria, which would be the first deployment of an AI-driven vaccination uptake program in the country and hopefully, pave the way for other data-driven programs to improve health outcomes in Nigeria.
Causal Bandits on General Graphs
Jul 06, 2021
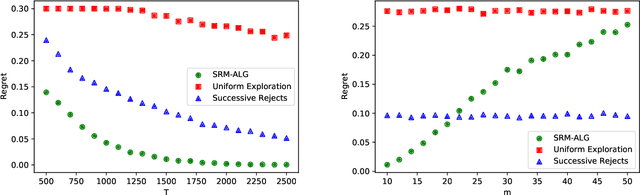
Abstract:We study the problem of determining the best intervention in a Causal Bayesian Network (CBN) specified only by its causal graph. We model this as a stochastic multi-armed bandit (MAB) problem with side-information, where the interventions correspond to the arms of the bandit instance. First, we propose a simple regret minimization algorithm that takes as input a semi-Markovian causal graph with atomic interventions and possibly unobservable variables, and achieves $\tilde{O}(\sqrt{M/T})$ expected simple regret, where $M$ is dependent on the input CBN and could be very small compared to the number of arms. We also show that this is almost optimal for CBNs described by causal graphs having an $n$-ary tree structure. Our simple regret minimization results, both upper and lower bound, subsume previous results in the literature, which assumed additional structural restrictions on the input causal graph. In particular, our results indicate that the simple regret guarantee of our proposed algorithm can only be improved by considering more nuanced structural restrictions on the causal graph. Next, we propose a cumulative regret minimization algorithm that takes as input a general causal graph with all observable nodes and atomic interventions and performs better than the optimal MAB algorithm that does not take causal side-information into account. We also experimentally compare both our algorithms with the best known algorithms in the literature. To the best of our knowledge, this work gives the first simple and cumulative regret minimization algorithms for CBNs with general causal graphs under atomic interventions and having unobserved confounders.
Strategic Classification in the Dark
Mar 06, 2021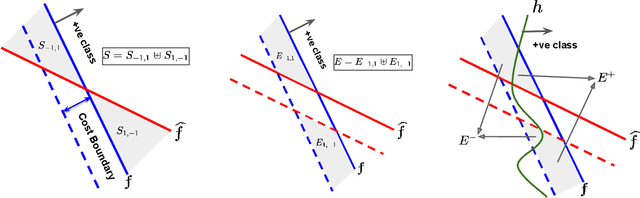
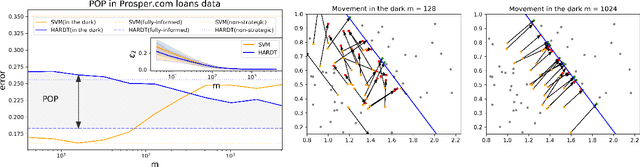
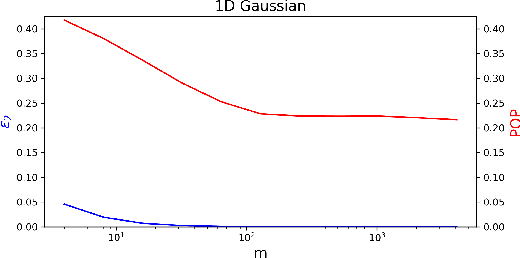
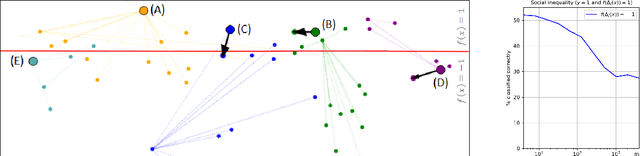
Abstract:Strategic classification studies the interaction between a classification rule and the strategic agents it governs. Under the assumption that the classifier is known, rational agents respond to it by manipulating their features. However, in many real-life scenarios of high-stake classification (e.g., credit scoring), the classifier is not revealed to the agents, which leads agents to attempt to learn the classifier and game it too. In this paper we generalize the strategic classification model to such scenarios. We define the price of opacity as the difference in prediction error between opaque and transparent strategy-robust classifiers, characterize it, and give a sufficient condition for this price to be strictly positive, in which case transparency is the recommended policy. Our experiments show how Hardt et al.'s robust classifier is affected by keeping agents in the dark.
State-Visitation Fairness in Average-Reward MDPs
Mar 02, 2021
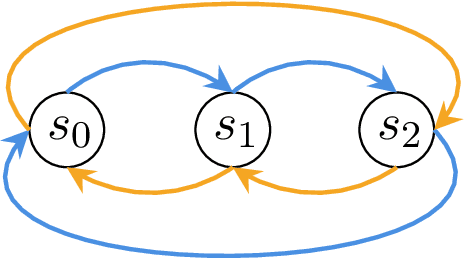
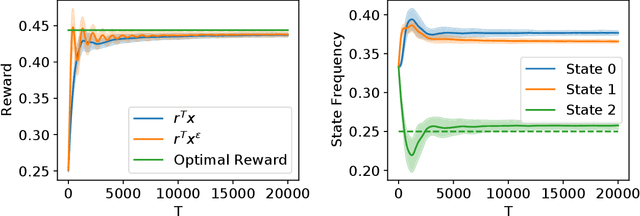
Abstract:Fairness has emerged as an important concern in automated decision-making in recent years, especially when these decisions affect human welfare. In this work, we study fairness in temporally extended decision-making settings, specifically those formulated as Markov Decision Processes (MDPs). Our proposed notion of fairness ensures that each state's long-term visitation frequency is more than a specified fraction. In an average-reward MDP (AMDP) setting, we formulate the problem as a bilinear saddle point program and, for a generative model, solve it using a Stochastic Mirror Descent (SMD) based algorithm. The proposed solution guarantees a simultaneous approximation on the expected average-reward and the long-term state-visitation frequency. We validate our theoretical results with experiments on synthetic data.
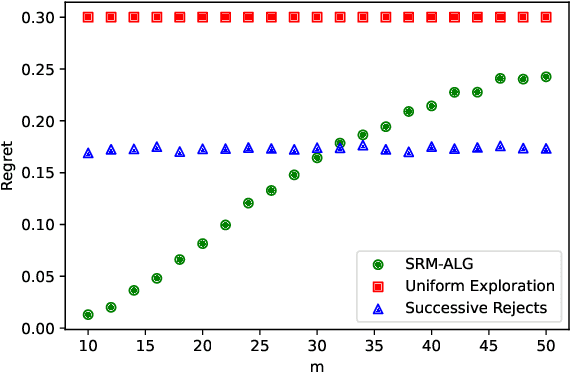
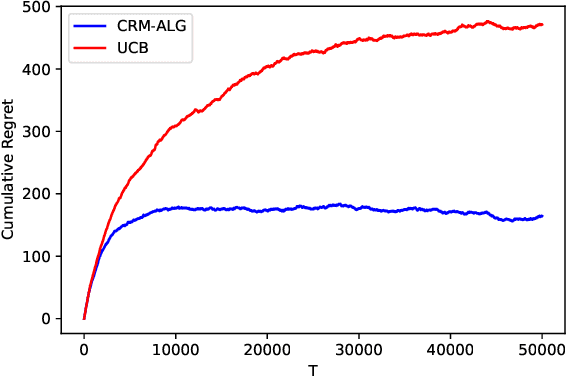
Budgeted and Non-budgeted Causal Bandits
Dec 13, 2020
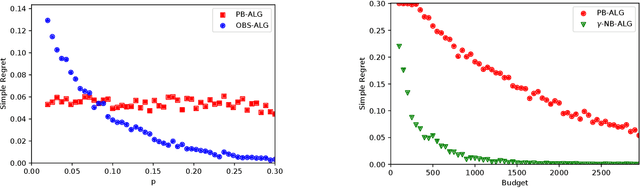
Abstract:Learning good interventions in a causal graph can be modelled as a stochastic multi-armed bandit problem with side-information. First, we study this problem when interventions are more expensive than observations and a budget is specified. If there are no backdoor paths from an intervenable node to the reward node then we propose an algorithm to minimize simple regret that optimally trades-off observations and interventions based on the cost of intervention. We also propose an algorithm that accounts for the cost of interventions, utilizes causal side-information, and minimizes the expected cumulative regret without exceeding the budget. Our cumulative-regret minimization algorithm performs better than standard algorithms that do not take side-information into account. Finally, we study the problem of learning best interventions without budget constraint in general graphs and give an algorithm that achieves constant expected cumulative regret in terms of the instance parameters when the parent distribution of the reward variable for each intervention is known. Our results are experimentally validated and compared to the best-known bounds in the current literature.
Sparse Linear Networks with a Fixed Butterfly Structure: Theory and Practice
Jul 17, 2020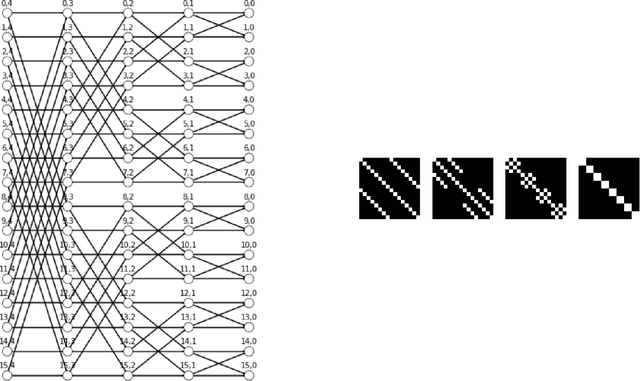

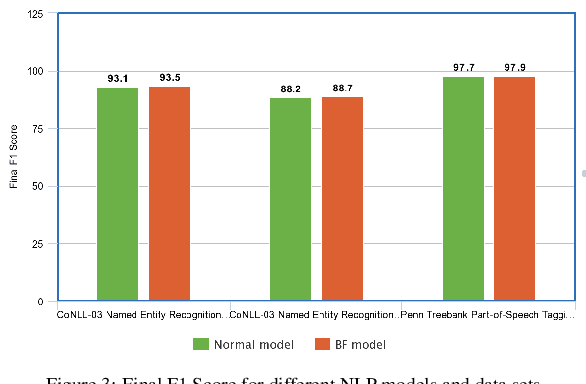

Abstract:Fast Fourier transform, Wavelets, and other well-known transforms in signal processing have a structured representation as a product of sparse matrices which are referred to as butterfly structures. Research in the recent past have used such structured linear networks along with randomness as pre-conditioners to improve the computational performance of large scale linear algebraic operations. With the advent of deep learning and AI and the computational efficiency of such structured matrices, it is natural to study sparse linear deep networks in which the location of the non-zero weights are predetermined by the butterfly structure. This work studies, both theoretically and empirically, the feasibility of training such networks in different scenarios. Unlike convolutional neural networks, which are structured sparse networks designed to recognize local patterns in lattices representing a spatial or a temporal structure, the butterfly architecture used in this work can replace any dense linear operator with a gadget consisting of a sequence of logarithmically (in the network width) many sparse layers, containing a total of near linear number of weights. This improves on the quadratic number of weights required in a standard dense layer, with little compromise in expressibility of the resulting operator. We show in a collection of empirical experiments that our proposed architecture not only produces results that match and often outperform existing known architectures, but it also offers faster training and prediction in deployment. This empirical phenomenon is observed in a wide variety of experiments that we report, including both supervised prediction on NLP and vision data, as well as in unsupervised representation learning using autoencoders. Preliminary theoretical results presented in the paper explain why training speed and outcome are not compromised by our proposed approach.
Achieving Fairness in the Stochastic Multi-armed Bandit Problem
Jul 23, 2019
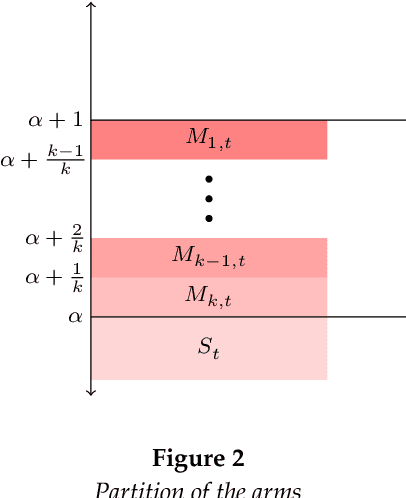
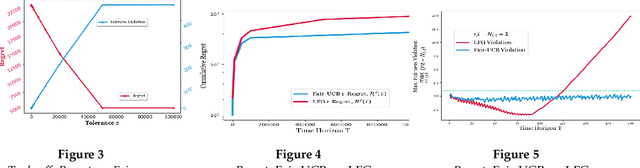
Abstract:We study an interesting variant of the stochastic multi-armed bandit problem, called the Fair-SMAB problem, where each arm is required to be pulled for at least a given fraction of the total available rounds. We investigate the interplay between learning and fairness in terms of a pre-specified vector denoting the fractions of guaranteed pulls. We define a fairness-aware regret, called $r$-Regret, that takes into account the above fairness constraints and naturally extends the conventional notion of regret. Our primary contribution is characterizing a class of Fair-SMAB algorithms by two parameters: the unfairness tolerance and the learning algorithm used as a black-box. We provide a fairness guarantee for this class that holds uniformly over time irrespective of the choice of the learning algorithm. In particular, when the learning algorithm is UCB1, we show that our algorithm achieves $O(\ln T)$ $r$-Regret. Finally, we evaluate the cost of fairness in terms of the conventional notion of regret.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge