Vishakha Patil
Mitigating Disparity while Maximizing Reward: Tight Anytime Guarantee for Improving Bandits
Aug 19, 2022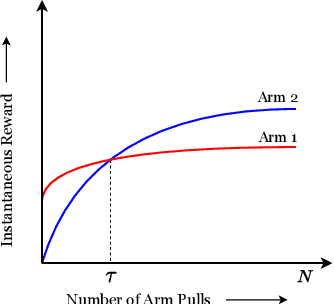
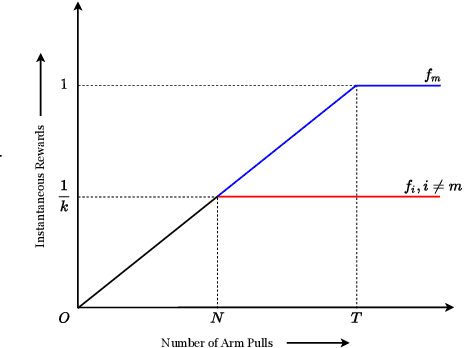
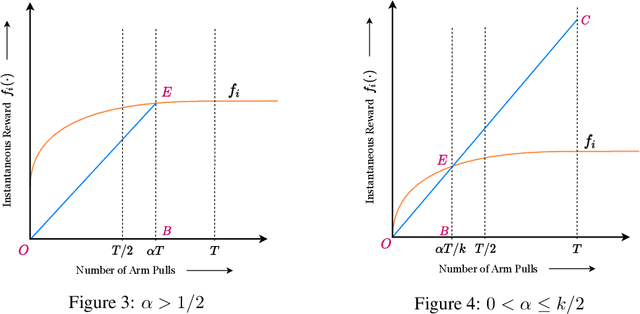
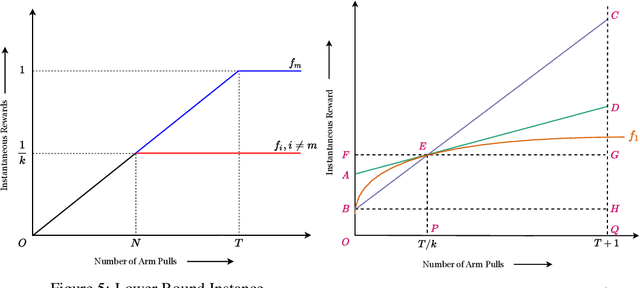
Abstract:We study the Improving Multi-Armed Bandit (IMAB) problem, where the reward obtained from an arm increases with the number of pulls it receives. This model provides an elegant abstraction for many real-world problems in domains such as education and employment, where decisions about the distribution of opportunities can affect the future capabilities of communities and the disparity between them. A decision-maker in such settings must consider the impact of her decisions on future rewards in addition to the standard objective of maximizing her cumulative reward at any time. In many of these applications, the time horizon is unknown to the decision-maker beforehand, which motivates the study of the IMAB problem in the technically more challenging horizon-unaware setting. We study the tension that arises between two seemingly conflicting objectives in the horizon-unaware setting: a) maximizing the cumulative reward at any time based on current rewards of the arms, and b) ensuring that arms with better long-term rewards get sufficient opportunities even if they initially have low rewards. We show that, surprisingly, the two objectives are aligned with each other in this setting. Our main contribution is an anytime algorithm for the IMAB problem that achieves the best possible cumulative reward while ensuring that the arms reach their true potential given sufficient time. Our algorithm mitigates the initial disparity due to lack of opportunity and continues pulling an arm till it stops improving. We prove the optimality of our algorithm by showing that a) any algorithm for the IMAB problem, no matter how utilitarian, must suffer $\Omega(T)$ policy regret and $\Omega(k)$ competitive ratio with respect to the optimal offline policy, and b) the competitive ratio of our algorithm is $O(k)$.
State-Visitation Fairness in Average-Reward MDPs
Mar 02, 2021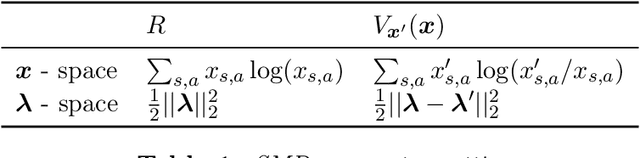
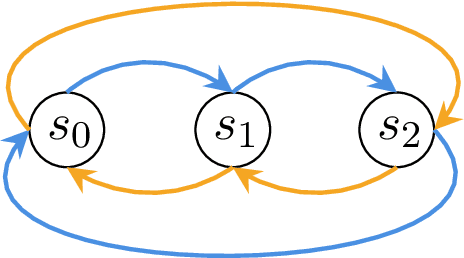
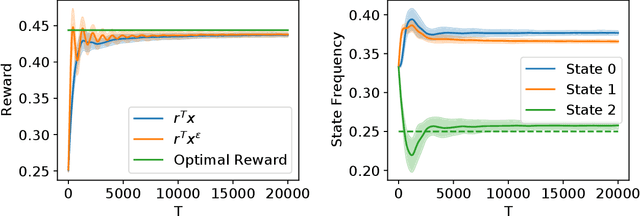
Abstract:Fairness has emerged as an important concern in automated decision-making in recent years, especially when these decisions affect human welfare. In this work, we study fairness in temporally extended decision-making settings, specifically those formulated as Markov Decision Processes (MDPs). Our proposed notion of fairness ensures that each state's long-term visitation frequency is more than a specified fraction. In an average-reward MDP (AMDP) setting, we formulate the problem as a bilinear saddle point program and, for a generative model, solve it using a Stochastic Mirror Descent (SMD) based algorithm. The proposed solution guarantees a simultaneous approximation on the expected average-reward and the long-term state-visitation frequency. We validate our theoretical results with experiments on synthetic data.
Budgeted and Non-budgeted Causal Bandits
Dec 13, 2020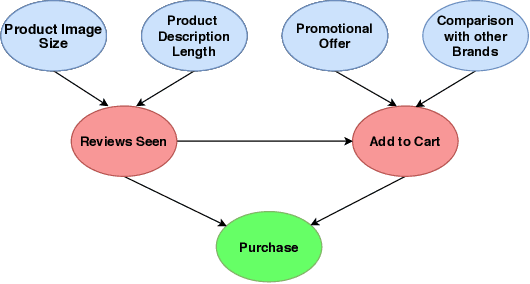
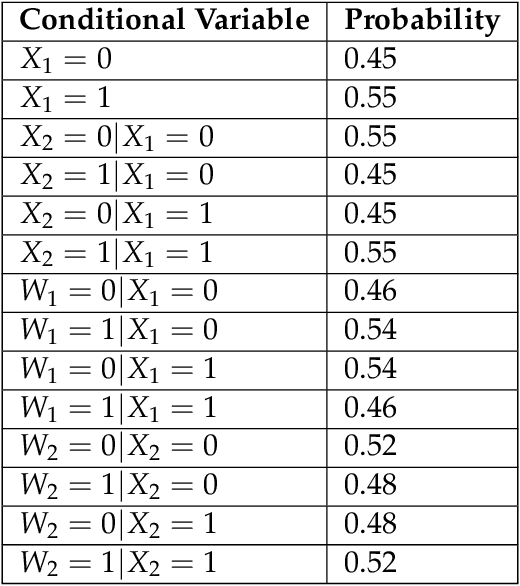
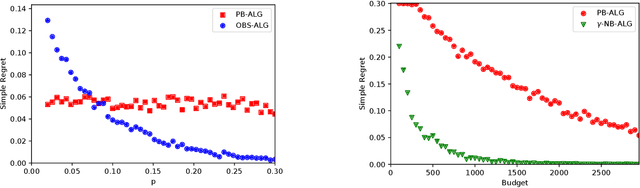
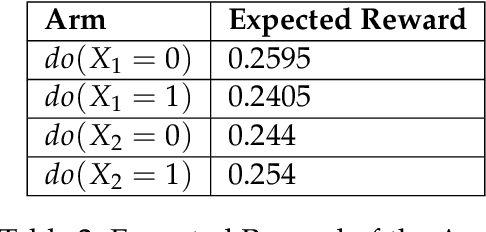
Abstract:Learning good interventions in a causal graph can be modelled as a stochastic multi-armed bandit problem with side-information. First, we study this problem when interventions are more expensive than observations and a budget is specified. If there are no backdoor paths from an intervenable node to the reward node then we propose an algorithm to minimize simple regret that optimally trades-off observations and interventions based on the cost of intervention. We also propose an algorithm that accounts for the cost of interventions, utilizes causal side-information, and minimizes the expected cumulative regret without exceeding the budget. Our cumulative-regret minimization algorithm performs better than standard algorithms that do not take side-information into account. Finally, we study the problem of learning best interventions without budget constraint in general graphs and give an algorithm that achieves constant expected cumulative regret in terms of the instance parameters when the parent distribution of the reward variable for each intervention is known. Our results are experimentally validated and compared to the best-known bounds in the current literature.
Streaming Algorithms for Stochastic Multi-armed Bandits
Dec 09, 2020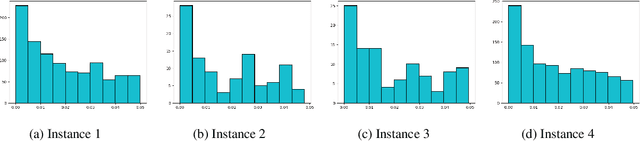

Abstract:We study the Stochastic Multi-armed Bandit problem under bounded arm-memory. In this setting, the arms arrive in a stream, and the number of arms that can be stored in the memory at any time, is bounded. The decision-maker can only pull arms that are present in the memory. We address the problem from the perspective of two standard objectives: 1) regret minimization, and 2) best-arm identification. For regret minimization, we settle an important open question by showing an almost tight hardness. We show {\Omega}(T^{2/3}) cumulative regret in expectation for arm-memory size of (n-1), where n is the number of arms. For best-arm identification, we study two algorithms. First, we present an O(r) arm-memory r-round adaptive streaming algorithm to find an {\epsilon}-best arm. In r-round adaptive streaming algorithm for best-arm identification, the arm pulls in each round are decided based on the observed outcomes in the earlier rounds. The best-arm is the output at the end of r rounds. The upper bound on the sample complexity of our algorithm matches with the lower bound for any r-round adaptive streaming algorithm. Secondly, we present a heuristic to find the {\epsilon}-best arm with optimal sample complexity, by storing only one extra arm in the memory.
Achieving Fairness in the Stochastic Multi-armed Bandit Problem
Jul 23, 2019
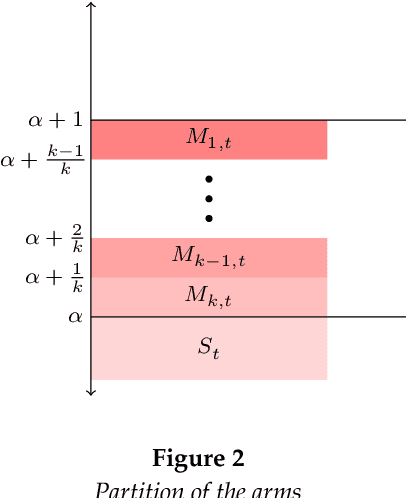
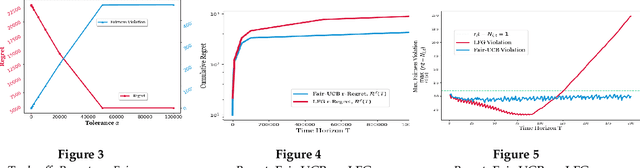
Abstract:We study an interesting variant of the stochastic multi-armed bandit problem, called the Fair-SMAB problem, where each arm is required to be pulled for at least a given fraction of the total available rounds. We investigate the interplay between learning and fairness in terms of a pre-specified vector denoting the fractions of guaranteed pulls. We define a fairness-aware regret, called $r$-Regret, that takes into account the above fairness constraints and naturally extends the conventional notion of regret. Our primary contribution is characterizing a class of Fair-SMAB algorithms by two parameters: the unfairness tolerance and the learning algorithm used as a black-box. We provide a fairness guarantee for this class that holds uniformly over time irrespective of the choice of the learning algorithm. In particular, when the learning algorithm is UCB1, we show that our algorithm achieves $O(\ln T)$ $r$-Regret. Finally, we evaluate the cost of fairness in terms of the conventional notion of regret.
Stochastic Multi-armed Bandits with Arm-specific Fairness Guarantees
May 27, 2019


Abstract:We study an interesting variant of the stochastic multi-armed bandit problem in which each arm is required to be pulled for at least a given fraction of the total available rounds. We investigate the interplay between learning and fairness in terms of a pre-specified vector specifying the fractions of guaranteed pulls. We define a Fairness-aware regret that takes into account the above fairness constraints and extends the conventional notion of regret in a natural way. We show that logarithmic regret can be achieved while (almost) satisfying the fairness requirements. In contrast to the current literature where the fairness notion is instance dependent, we consider that the fairness criterion is exogenously specified as an input to the algorithm. Our regret guarantee is universal i.e. holds for any given fairness vector.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge