Lipschitz Dueling Bandits over Continuous Action Spaces

We study for the first time, stochastic dueling bandits over continuous action spaces with Lipschitz structure, where feedback is purely comparative. While dueling bandits and Lipschitz bandits have been studied separately, their combination has remained unexplored. We propose the first algorithm for Lipschitz dueling bandits, using round-based exploration and recursive region elimination guided by an adaptive reference arm. We develop new analytical tools for relative feedback and prove a regret bound of $\tilde O\left(T^{\frac{d_z+1}{d_z+2}}\right)$, where $d_z$ is the zooming dimension of the near-optimal region. Further, our algorithm takes only logarithmic space in terms of the total time horizon, best achievable by any bandit algorithm over a continuous action space.

Multi-agent Multi-armed Bandits with Minimum Reward Guarantee Fairness

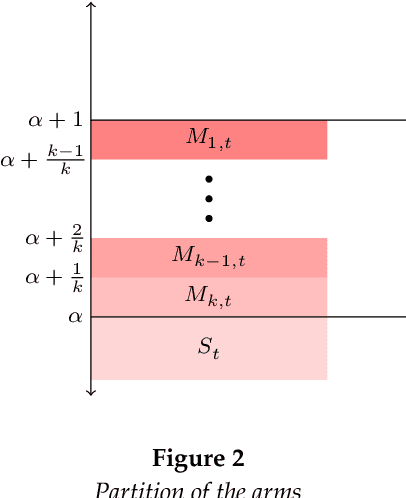
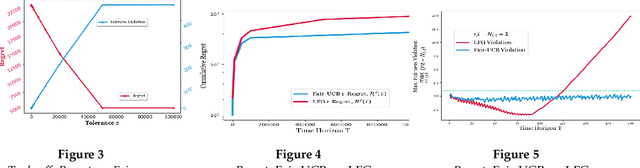
We investigate the problem of maximizing social welfare while ensuring fairness in a multi-agent multi-armed bandit (MA-MAB) setting. In this problem, a centralized decision-maker takes actions over time, generating random rewards for various agents. Our goal is to maximize the sum of expected cumulative rewards, a.k.a. social welfare, while ensuring that each agent receives an expected reward that is at least a constant fraction of the maximum possible expected reward. Our proposed algorithm, RewardFairUCB, leverages the Upper Confidence Bound (UCB) technique to achieve sublinear regret bounds for both fairness and social welfare. The fairness regret measures the positive difference between the minimum reward guarantee and the expected reward of a given policy, whereas the social welfare regret measures the difference between the social welfare of the optimal fair policy and that of the given policy. We show that RewardFairUCB algorithm achieves instance-independent social welfare regret guarantees of $\tilde{O}(T^{1/2})$ and a fairness regret upper bound of $\tilde{O}(T^{3/4})$. We also give the lower bound of $\Omega(\sqrt{T})$ for both social welfare and fairness regret. We evaluate RewardFairUCB's performance against various baseline and heuristic algorithms using simulated data and real world data, highlighting trade-offs between fairness and social welfare regrets.

Simultaneously Achieving Group Exposure Fairness and Within-Group Meritocracy in Stochastic Bandits

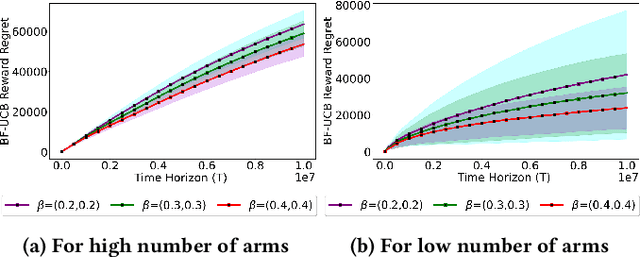
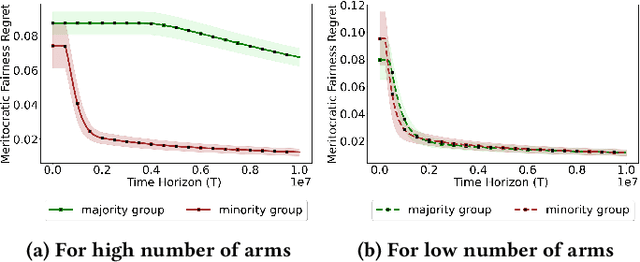
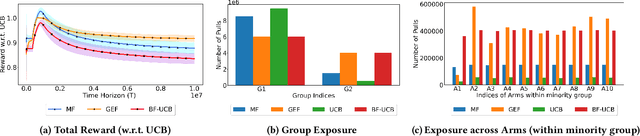
Existing approaches to fairness in stochastic multi-armed bandits (MAB) primarily focus on exposure guarantee to individual arms. When arms are naturally grouped by certain attribute(s), we propose Bi-Level Fairness, which considers two levels of fairness. At the first level, Bi-Level Fairness guarantees a certain minimum exposure to each group. To address the unbalanced allocation of pulls to individual arms within a group, we consider meritocratic fairness at the second level, which ensures that each arm is pulled according to its merit within the group. Our work shows that we can adapt a UCB-based algorithm to achieve a Bi-Level Fairness by providing (i) anytime Group Exposure Fairness guarantees and (ii) ensuring individual-level Meritocratic Fairness within each group. We first show that one can decompose regret bounds into two components: (a) regret due to anytime group exposure fairness and (b) regret due to meritocratic fairness within each group. Our proposed algorithm BF-UCB balances these two regrets optimally to achieve the upper bound of $O(\sqrt{T})$ on regret; $T$ being the stopping time. With the help of simulated experiments, we further show that BF-UCB achieves sub-linear regret; provides better group and individual exposure guarantees compared to existing algorithms; and does not result in a significant drop in reward with respect to UCB algorithm, which does not impose any fairness constraint.

Mitigating Disparity while Maximizing Reward: Tight Anytime Guarantee for Improving Bandits

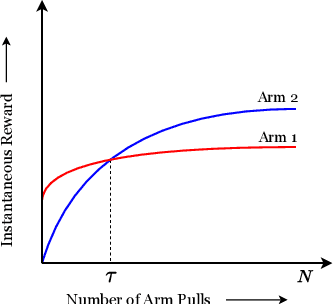
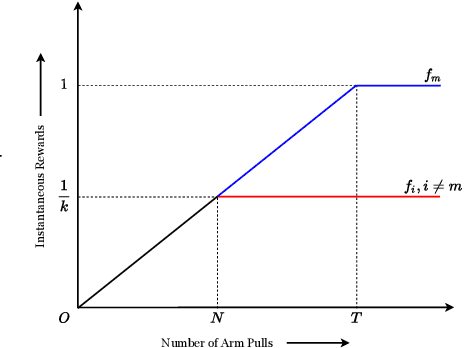
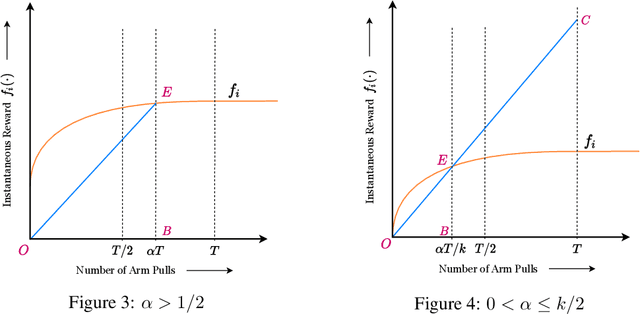
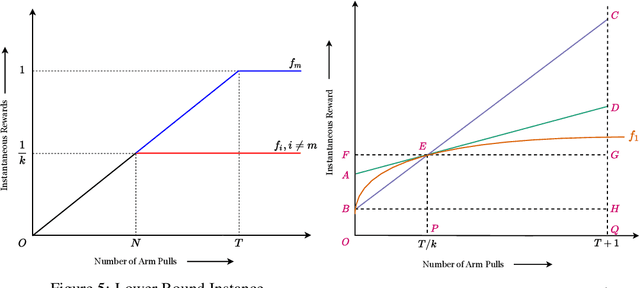
We study the Improving Multi-Armed Bandit (IMAB) problem, where the reward obtained from an arm increases with the number of pulls it receives. This model provides an elegant abstraction for many real-world problems in domains such as education and employment, where decisions about the distribution of opportunities can affect the future capabilities of communities and the disparity between them. A decision-maker in such settings must consider the impact of her decisions on future rewards in addition to the standard objective of maximizing her cumulative reward at any time. In many of these applications, the time horizon is unknown to the decision-maker beforehand, which motivates the study of the IMAB problem in the technically more challenging horizon-unaware setting. We study the tension that arises between two seemingly conflicting objectives in the horizon-unaware setting: a) maximizing the cumulative reward at any time based on current rewards of the arms, and b) ensuring that arms with better long-term rewards get sufficient opportunities even if they initially have low rewards. We show that, surprisingly, the two objectives are aligned with each other in this setting. Our main contribution is an anytime algorithm for the IMAB problem that achieves the best possible cumulative reward while ensuring that the arms reach their true potential given sufficient time. Our algorithm mitigates the initial disparity due to lack of opportunity and continues pulling an arm till it stops improving. We prove the optimality of our algorithm by showing that a) any algorithm for the IMAB problem, no matter how utilitarian, must suffer $\Omega(T)$ policy regret and $\Omega(k)$ competitive ratio with respect to the optimal offline policy, and b) the competitive ratio of our algorithm is $O(k)$.

Strategic Representation

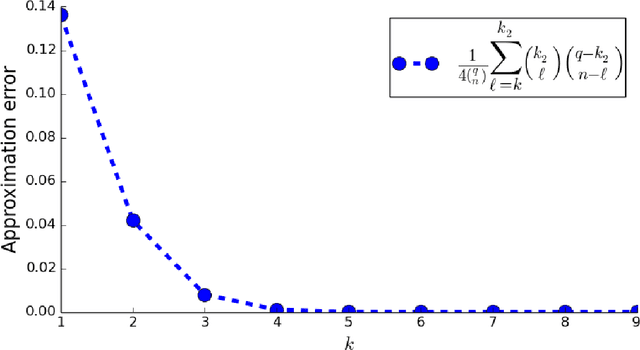
Humans have come to rely on machines for reducing excessive information to manageable representations. But this reliance can be abused -- strategic machines might craft representations that manipulate their users. How can a user make good choices based on strategic representations? We formalize this as a learning problem, and pursue algorithms for decision-making that are robust to manipulation. In our main setting of interest, the system represents attributes of an item to the user, who then decides whether or not to consume. We model this interaction through the lens of strategic classification (Hardt et al. 2016), reversed: the user, who learns, plays first; and the system, which responds, plays second. The system must respond with representations that reveal `nothing but the truth' but need not reveal the entire truth. Thus, the user faces the problem of learning set functions under strategic subset selection, which presents distinct algorithmic and statistical challenges. Our main result is a learning algorithm that minimizes error despite strategic representations, and our theoretical analysis sheds light on the trade-off between learning effort and susceptibility to manipulation.

Efficient Algorithms For Fair Clustering with a New Fairness Notion

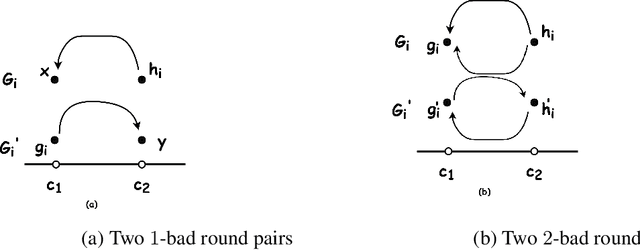
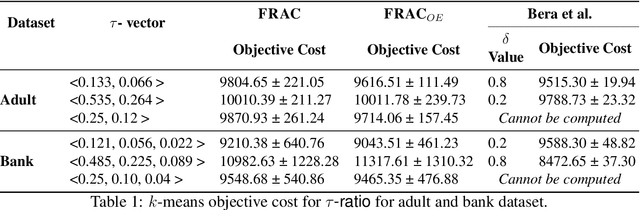
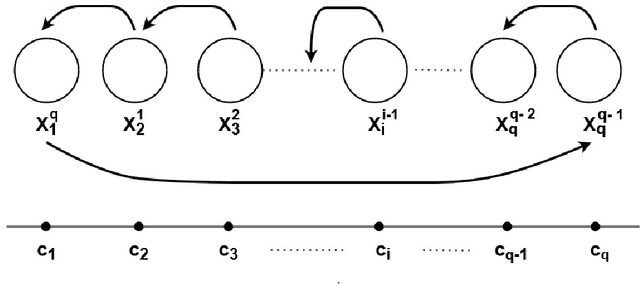
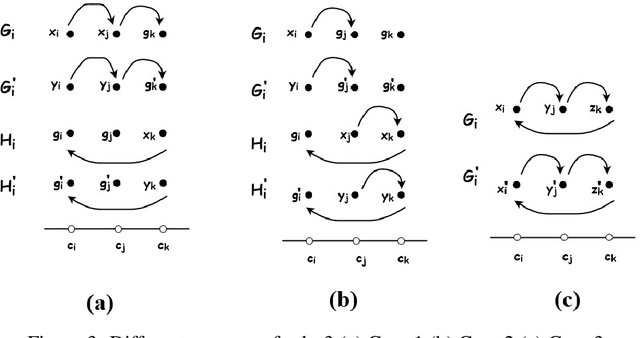
We revisit the problem of fair clustering, first introduced by Chierichetti et al., that requires each protected attribute to have approximately equal representation in every cluster; i.e., a balance property. Existing solutions to fair clustering are either not scalable or do not achieve an optimal trade-off between clustering objective and fairness. In this paper, we propose a new notion of fairness, which we call $tau$-fair fairness, that strictly generalizes the balance property and enables a fine-grained efficiency vs. fairness trade-off. Furthermore, we show that simple greedy round-robin based algorithms achieve this trade-off efficiently. Under a more general setting of multi-valued protected attributes, we rigorously analyze the theoretical properties of the our algorithms. Our experimental results suggest that the proposed solution outperforms all the state-of-the-art algorithms and works exceptionally well even for a large number of clusters.

Sleeping Combinatorial Bandits

In this paper, we study an interesting combination of sleeping and combinatorial stochastic bandits. In the mixed model studied here, at each discrete time instant, an arbitrary \emph{availability set} is generated from a fixed set of \emph{base} arms. An algorithm can select a subset of arms from the \emph{availability set} (sleeping bandits) and receive the corresponding reward along with semi-bandit feedback (combinatorial bandits). We adapt the well-known CUCB algorithm in the sleeping combinatorial bandits setting and refer to it as \CSUCB. We prove -- under mild smoothness conditions -- that the \CSUCB\ algorithm achieves an $O(\log (T))$ instance-dependent regret guarantee. We further prove that (i) when the range of the rewards is bounded, the regret guarantee of \CSUCB\ algorithm is $O(\sqrt{T \log (T)})$ and (ii) the instance-independent regret is $O(\sqrt[3]{T^2 \log(T)})$ in a general setting. Our results are quite general and hold under general environments -- such as non-additive reward functions, volatile arm availability, a variable number of base-arms to be pulled -- arising in practical applications. We validate the proven theoretical guarantees through experiments.

Strategic Classification in the Dark

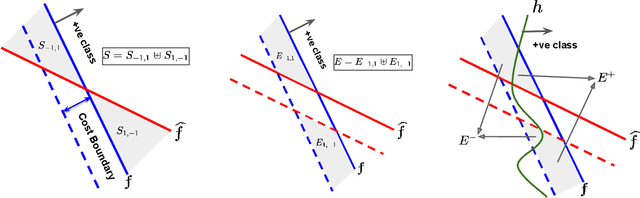
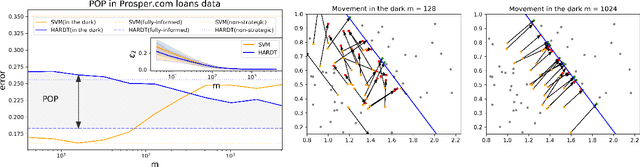
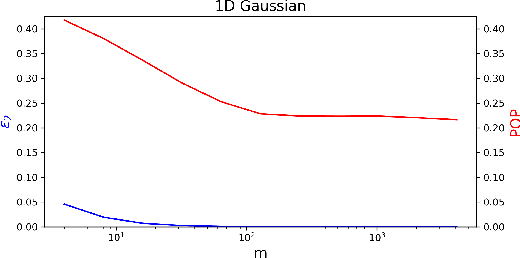
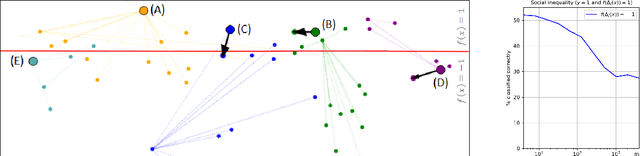
Strategic classification studies the interaction between a classification rule and the strategic agents it governs. Under the assumption that the classifier is known, rational agents respond to it by manipulating their features. However, in many real-life scenarios of high-stake classification (e.g., credit scoring), the classifier is not revealed to the agents, which leads agents to attempt to learn the classifier and game it too. In this paper we generalize the strategic classification model to such scenarios. We define the price of opacity as the difference in prediction error between opaque and transparent strategy-robust classifiers, characterize it, and give a sufficient condition for this price to be strictly positive, in which case transparency is the recommended policy. Our experiments show how Hardt et al.'s robust classifier is affected by keeping agents in the dark.

State-Visitation Fairness in Average-Reward MDPs

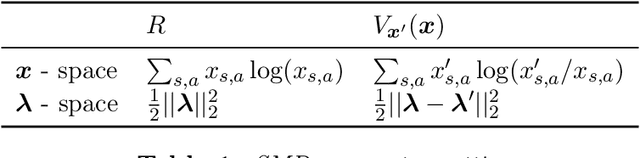
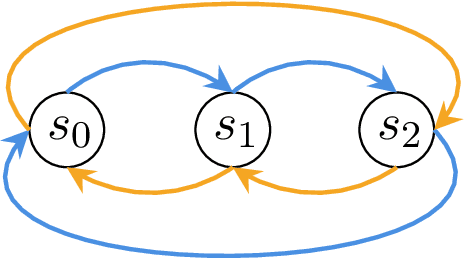
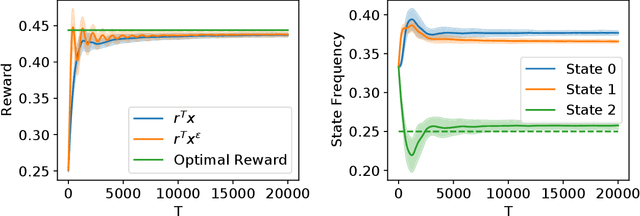
Fairness has emerged as an important concern in automated decision-making in recent years, especially when these decisions affect human welfare. In this work, we study fairness in temporally extended decision-making settings, specifically those formulated as Markov Decision Processes (MDPs). Our proposed notion of fairness ensures that each state's long-term visitation frequency is more than a specified fraction. In an average-reward MDP (AMDP) setting, we formulate the problem as a bilinear saddle point program and, for a generative model, solve it using a Stochastic Mirror Descent (SMD) based algorithm. The proposed solution guarantees a simultaneous approximation on the expected average-reward and the long-term state-visitation frequency. We validate our theoretical results with experiments on synthetic data.

Ballooning Multi-Armed Bandits

In this paper, we introduce Ballooning Multi-Armed Bandits (BL-MAB), a novel extension to the classical stochastic MAB model. In BL-MAB model, the set of available arms grows (or balloons) over time. In contrast to the classical MAB setting where the regret is computed with respect to the best arm overall, the regret in a BL-MAB setting is computed with respect to the best available arm at each time. We first observe that the existing MAB algorithms are not regret-optimal for the BL-MAB model. We show that if the best arm is equally likely to arrive at any time, a sub-linear regret cannot be achieved, irrespective of the arrival of other arms. We further show that if the best arm is more likely to arrive in the early rounds, one can achieve sub-linear regret. Our proposed algorithm determines (1) the fraction of the time horizon for which the newly arriving arms should be explored and (2) the sequence of arm pulls in the exploitation phase from among the explored arms. Making reasonable assumptions on the arrival distribution of the best arm in terms of the thinness of the distribution's tail, we prove that the proposed algorithm achieves sub-linear instance-independent regret. We further quantify the explicit dependence of regret on the arrival distribution parameters. We reinforce our theoretical findings with extensive simulation results.