Welfarist Formulations for Diverse Similarity Search

Nearest Neighbor Search (NNS) is a fundamental problem in data structures with wide-ranging applications, such as web search, recommendation systems, and, more recently, retrieval-augmented generations (RAG). In such recent applications, in addition to the relevance (similarity) of the returned neighbors, diversity among the neighbors is a central requirement. In this paper, we develop principled welfare-based formulations in NNS for realizing diversity across attributes. Our formulations are based on welfare functions -- from mathematical economics -- that satisfy central diversity (fairness) and relevance (economic efficiency) axioms. With a particular focus on Nash social welfare, we note that our welfare-based formulations provide objective functions that adaptively balance relevance and diversity in a query-dependent manner. Notably, such a balance was not present in the prior constraint-based approach, which forced a fixed level of diversity and optimized for relevance. In addition, our formulation provides a parametric way to control the trade-off between relevance and diversity, providing practitioners with flexibility to tailor search results to task-specific requirements. We develop efficient nearest neighbor algorithms with provable guarantees for the welfare-based objectives. Notably, our algorithm can be applied on top of any standard ANN method (i.e., use standard ANN method as a subroutine) to efficiently find neighbors that approximately maximize our welfare-based objectives. Experimental results demonstrate that our approach is practical and substantially improves diversity while maintaining high relevance of the retrieved neighbors.

Posterior Sampling by Combining Diffusion Models with Annealed Langevin Dynamics

Given a noisy linear measurement $y = Ax + \xi$ of a distribution $p(x)$, and a good approximation to the prior $p(x)$, when can we sample from the posterior $p(x \mid y)$? Posterior sampling provides an accurate and fair framework for tasks such as inpainting, deblurring, and MRI reconstruction, and several heuristics attempt to approximate it. Unfortunately, approximate posterior sampling is computationally intractable in general. To sidestep this hardness, we focus on (local or global) log-concave distributions $p(x)$. In this regime, Langevin dynamics yields posterior samples when the exact scores of $p(x)$ are available, but it is brittle to score--estimation error, requiring an MGF bound (sub-exponential error). By contrast, in the unconditional setting, diffusion models succeed with only an $L^2$ bound on the score error. We prove that combining diffusion models with an annealed variant of Langevin dynamics achieves conditional sampling in polynomial time using merely an $L^4$ bound on the score error.

AutoChemSchematic AI: A Closed-Loop, Physics-Aware Agentic Framework for Auto-Generating Chemical Process and Instrumentation Diagrams

Recent advancements in generative AI have accelerated the discovery of novel chemicals and materials; however, transitioning these discoveries to industrial-scale production remains a critical bottleneck, as it requires the development of entirely new chemical manufacturing processes. Current AI methods cannot auto-generate PFDs or PIDs, despite their critical role in scaling chemical processes, while adhering to engineering constraints. We present a closed loop, physics aware framework for the automated generation of industrially viable PFDs and PIDs. The framework integrates domain specialized small scale language models (SLMs) (trained for chemical process QA tasks) with first principles simulation, leveraging three key components: (1) a hierarchical knowledge graph of process flow and instrumentation descriptions for 1,020+ chemicals, (2) a multi-stage training pipeline that fine tunes domain specialized SLMs on synthetic datasets via Supervised Fine-Tuning (SFT), Direct Preference Optimization (DPO), and Retrieval-Augmented Instruction Tuning (RAIT), and (3) DWSIM based simulator in the loop validation to ensure feasibility. To improve both runtime efficiency and model compactness, the framework incorporates advanced inference time optimizations including FlashAttention, Lookahead Decoding, PagedAttention with KV-cache quantization, and Test Time Inference Scaling and independently applies structural pruning techniques (width and depth) guided by importance heuristics to reduce model size with minimal accuracy loss. Experiments demonstrate that the framework generates simulator-validated process descriptions with high fidelity, outperforms baseline methods in correctness, and generalizes to unseen chemicals. By bridging AI-driven design with industrial-scale feasibility, this work significantly reduces R&D timelines from lab discovery to plant deployment.

Agentic Multimodal AI for Hyperpersonalized B2B and B2C Advertising in Competitive Markets: An AI-Driven Competitive Advertising Framework

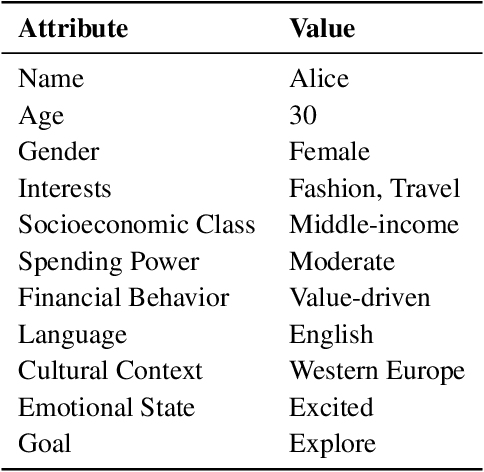
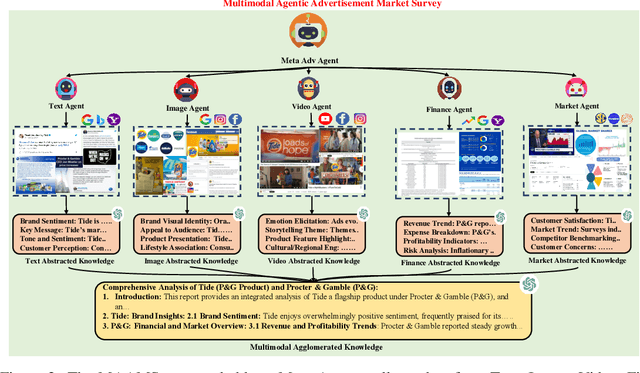
The growing use of foundation models (FMs) in real-world applications demands adaptive, reliable, and efficient strategies for dynamic markets. In the chemical industry, AI-discovered materials drive innovation, but commercial success hinges on market adoption, requiring FM-driven advertising frameworks that operate in-the-wild. We present a multilingual, multimodal AI framework for autonomous, hyper-personalized advertising in B2B and B2C markets. By integrating retrieval-augmented generation (RAG), multimodal reasoning, and adaptive persona-based targeting, our system generates culturally relevant, market-aware ads tailored to shifting consumer behaviors and competition. Validation combines real-world product experiments with a Simulated Humanistic Colony of Agents to model consumer personas, optimize strategies at scale, and ensure privacy compliance. Synthetic experiments mirror real-world scenarios, enabling cost-effective testing of ad strategies without risky A/B tests. Combining structured retrieval-augmented reasoning with in-context learning (ICL), the framework boosts engagement, prevents market cannibalization, and maximizes ROAS. This work bridges AI-driven innovation and market adoption, advancing multimodal FM deployment for high-stakes decision-making in commercial marketing.

Accelerating Manufacturing Scale-Up from Material Discovery Using Agentic Web Navigation and Retrieval-Augmented AI for Process Engineering Schematics Design

Process Flow Diagrams (PFDs) and Process and Instrumentation Diagrams (PIDs) are critical tools for industrial process design, control, and safety. However, the generation of precise and regulation-compliant diagrams remains a significant challenge, particularly in scaling breakthroughs from material discovery to industrial production in an era of automation and digitalization. This paper introduces an autonomous agentic framework to address these challenges through a twostage approach involving knowledge acquisition and generation. The framework integrates specialized sub-agents for retrieving and synthesizing multimodal data from publicly available online sources and constructs ontological knowledge graphs using a Graph Retrieval-Augmented Generation (Graph RAG) paradigm. These capabilities enable the automation of diagram generation and open-domain question answering (ODQA) tasks with high contextual accuracy. Extensive empirical experiments demonstrate the frameworks ability to deliver regulation-compliant diagrams with minimal expert intervention, highlighting its practical utility for industrial applications.

Multi-Source Knowledge-Based Hybrid Neural Framework for Time Series Representation Learning

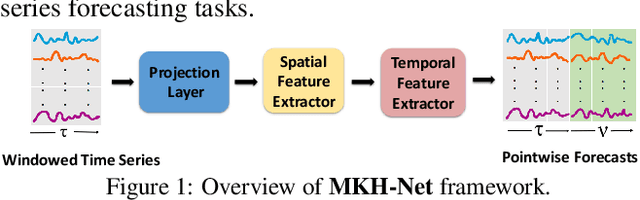
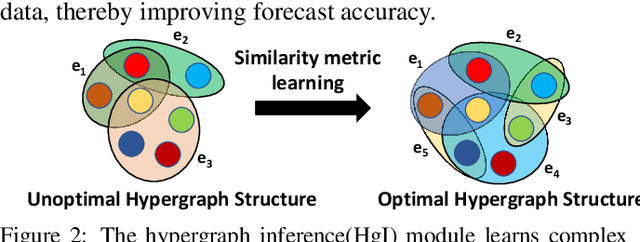
Accurately predicting the behavior of complex dynamical systems, characterized by high-dimensional multivariate time series(MTS) in interconnected sensor networks, is crucial for informed decision-making in various applications to minimize risk. While graph forecasting networks(GFNs) are ideal for forecasting MTS data that exhibit spatio-temporal dependencies, prior works rely solely on the domain-specific knowledge of time-series variables inter-relationships to model the nonlinear dynamics, neglecting inherent relational structural dependencies among the variables within the MTS data. In contrast, contemporary works infer relational structures from MTS data but neglect domain-specific knowledge. The proposed hybrid architecture addresses these limitations by combining both domain-specific knowledge and implicit knowledge of the relational structure underlying the MTS data using Knowledge-Based Compositional Generalization. The hybrid architecture shows promising results on multiple benchmark datasets, outperforming state-of-the-art forecasting methods. Additionally, the architecture models the time varying uncertainty of multi-horizon forecasts.

Multi-Knowledge Fusion Network for Time Series Representation Learning

Forecasting the behaviour of complex dynamical systems such as interconnected sensor networks characterized by high-dimensional multivariate time series(MTS) is of paramount importance for making informed decisions and planning for the future in a broad spectrum of applications. Graph forecasting networks(GFNs) are well-suited for forecasting MTS data that exhibit spatio-temporal dependencies. However, most prior works of GFN-based methods on MTS forecasting rely on domain-expertise to model the nonlinear dynamics of the system, but neglect the potential to leverage the inherent relational-structural dependencies among time series variables underlying MTS data. On the other hand, contemporary works attempt to infer the relational structure of the complex dependencies between the variables and simultaneously learn the nonlinear dynamics of the interconnected system but neglect the possibility of incorporating domain-specific prior knowledge to improve forecast accuracy. To this end, we propose a hybrid architecture that combines explicit prior knowledge with implicit knowledge of the relational structure within the MTS data. It jointly learns intra-series temporal dependencies and inter-series spatial dependencies by encoding time-conditioned structural spatio-temporal inductive biases to provide more accurate and reliable forecasts. It also models the time-varying uncertainty of the multi-horizon forecasts to support decision-making by providing estimates of prediction uncertainty. The proposed architecture has shown promising results on multiple benchmark datasets and outperforms state-of-the-art forecasting methods by a significant margin. We report and discuss the ablation studies to validate our forecasting architecture.

Joint Hypergraph Rewiring and Memory-Augmented Forecasting Techniques in Digital Twin Technology

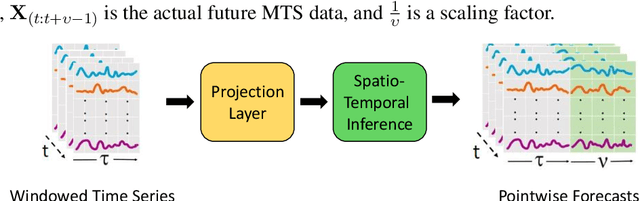
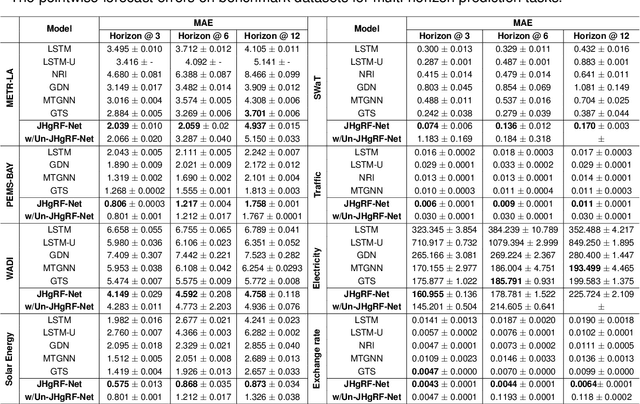
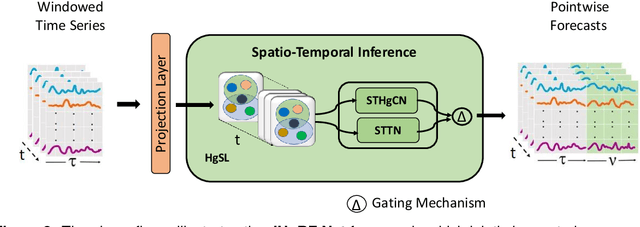
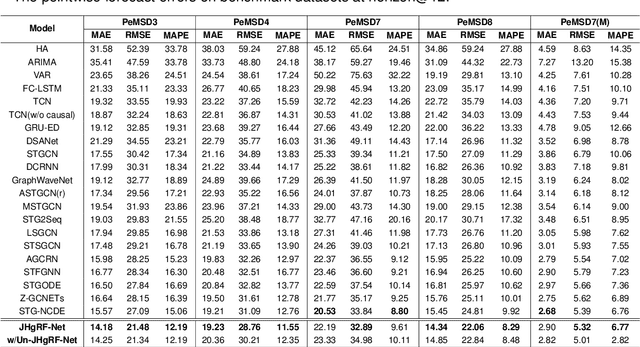
Digital Twin technology creates virtual replicas of physical objects, processes, or systems by replicating their properties, data, and behaviors. This advanced technology offers a range of intelligent functionalities, such as modeling, simulation, and data-driven decision-making, that facilitate design optimization, performance estimation, and monitoring operations. Forecasting plays a pivotal role in Digital Twin technology, as it enables the prediction of future outcomes, supports informed decision-making, minimizes risks, driving improvements in efficiency, productivity, and cost reduction. Recently, Digital Twin technology has leveraged Graph forecasting techniques in large-scale complex sensor networks to enable accurate forecasting and simulation of diverse scenarios, fostering proactive and data-driven decision making. However, existing Graph forecasting techniques lack scalability for many real-world applications. They have limited ability to adapt to non-stationary environments, retain past knowledge, lack a mechanism to capture the higher order spatio-temporal dynamics, and estimate uncertainty in model predictions. To surmount the challenges, we introduce a hybrid architecture that enhances the hypergraph representation learning backbone by incorporating fast adaptation to new patterns and memory-based retrieval of past knowledge. This balance aims to improve the slowly-learned backbone and achieve better performance in adapting to recent changes. In addition, it models the time-varying uncertainty of multi-horizon forecasts, providing estimates of prediction uncertainty. Our forecasting architecture has been validated through ablation studies and has demonstrated promising results across multiple benchmark datasets, surpassing state-ofthe-art forecasting methods by a significant margin.

Genetic Algorithm to Optimize Design of Micro-Surgical Scissors

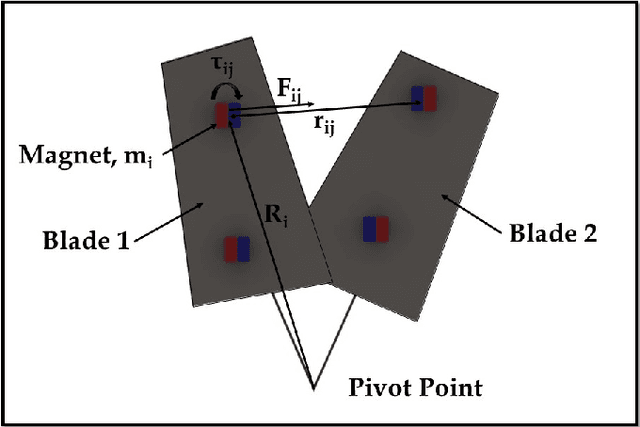
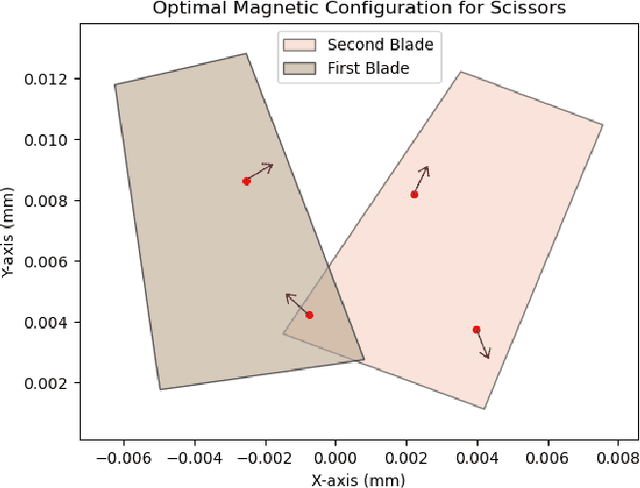
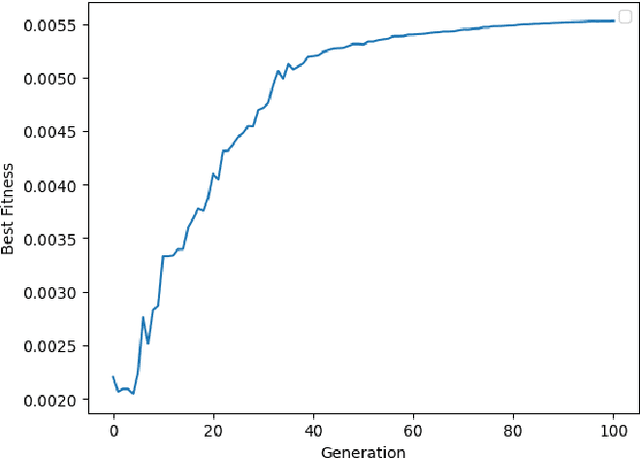
Microrobotics is an attractive area of research as small-scale robots have the potential to improve the precision and dexterity offered by minimally invasive surgeries. One example of such a tool is a pair of micro-surgical scissors that was developed for cutting of tumors or cancerous tissues present deep inside the body such as in the brain. This task is often deemed difficult or impossible with conventional robotic tools due to their size and dexterity. The scissors are designed with two magnets placed a specific distance apart to maximize deflection and generate cutting forces. However, remote actuation and size requirements of the micro-surgical scissors limits the force that can be generated to puncture the tissue. To address the limitation of small output forces, we use an evolutionary algorithm to further optimize the performance of the scissors. In this study, the design of the previously developed untethered micro-surgical scissors has been modified and their performance is enhanced by determining the optimal position of the magnets as well as the direction of each magnetic moment. The developed algorithm is successfully applied to a 4-magnet configuration which results in increased net torque. This improvement in net torque is directly translated into higher cutting forces. The new configuration generates a cutting force of 58 mN from 80 generations of the evolutionary algorithm which is a 1.65 times improvement from the original design. Furthermore, the developed algorithm has the advantage that it can be deployed with minor modifications to other microrobotic tools and systems, opening up new possibilities for various medical procedures and applications.

Fair Federated Data Clustering through Personalization: Bridging the Gap between Diverse Data Distributions

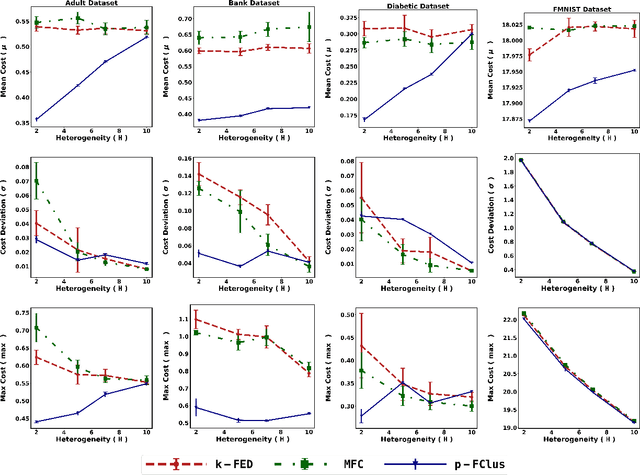
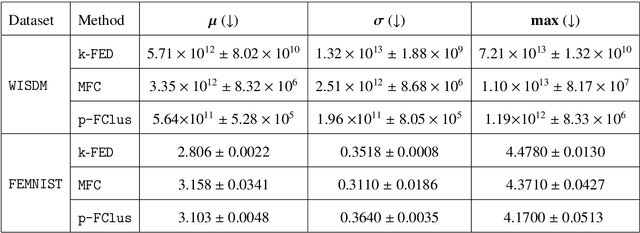
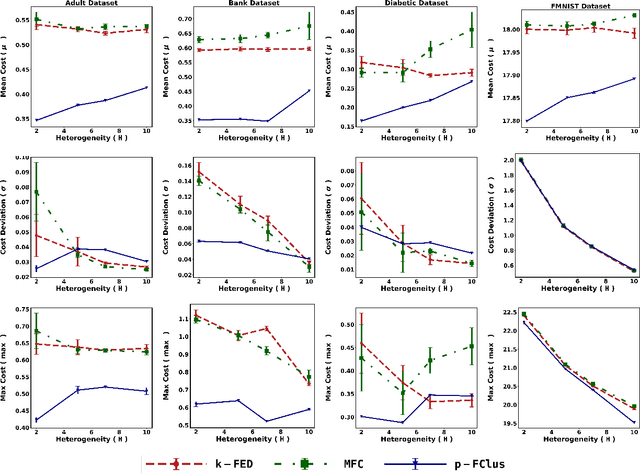
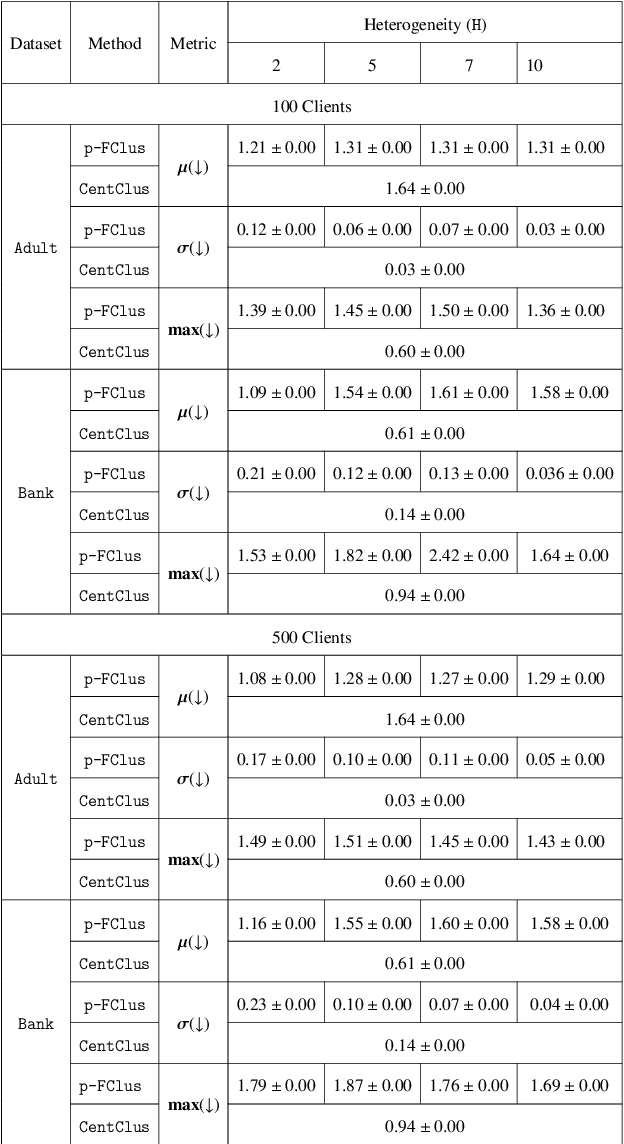
The rapid growth of data from edge devices has catalyzed the performance of machine learning algorithms. However, the data generated resides at client devices thus there are majorly two challenge faced by traditional machine learning paradigms - centralization of data for training and secondly for most the generated data the class labels are missing and there is very poor incentives to clients to manually label their data owing to high cost and lack of expertise. To overcome these issues, there have been initial attempts to handle unlabelled data in a privacy preserving distributed manner using unsupervised federated data clustering. The goal is partition the data available on clients into $k$ partitions (called clusters) without actual exchange of data. Most of the existing algorithms are highly dependent on data distribution patterns across clients or are computationally expensive. Furthermore, due to presence of skewed nature of data across clients in most of practical scenarios existing models might result in clients suffering high clustering cost making them reluctant to participate in federated process. To this, we are first to introduce the idea of personalization in federated clustering. The goal is achieve balance between achieving lower clustering cost and at same time achieving uniform cost across clients. We propose p-FClus that addresses these goal in a single round of communication between server and clients. We validate the efficacy of p-FClus against variety of federated datasets showcasing it's data independence nature, applicability to any finite $\ell$-norm, while simultaneously achieving lower cost and variance.