Double Blind Imaging with Generative Modeling

Blind inverse problems in imaging arise from uncertainties in the system used to collect (noisy) measurements of images. Recovering clean images from these measurements typically requires identifying the imaging system, either implicitly or explicitly. A common solution leverages generative models as priors for both the images and the imaging system parameters (e.g., a class of point spread functions). To learn these priors in a straightforward manner requires access to a dataset of clean images as well as samples of the imaging system. We propose an AmbientGAN-based generative technique to identify the distribution of parameters in unknown imaging systems, using only unpaired clean images and corrupted measurements. This learned distribution can then be used in model-based recovery algorithms to solve blind inverse problems such as blind deconvolution. We successfully demonstrate our technique for learning Gaussian blur and motion blur priors from noisy measurements and show their utility in solving blind deconvolution with diffusion posterior sampling.

Diffusion Posterior Sampling is Computationally Intractable

Diffusion models are a remarkably effective way of learning and sampling from a distribution $p(x)$. In posterior sampling, one is also given a measurement model $p(y \mid x)$ and a measurement $y$, and would like to sample from $p(x \mid y)$. Posterior sampling is useful for tasks such as inpainting, super-resolution, and MRI reconstruction, so a number of recent works have given algorithms to heuristically approximate it; but none are known to converge to the correct distribution in polynomial time. In this paper we show that posterior sampling is \emph{computationally intractable}: under the most basic assumption in cryptography -- that one-way functions exist -- there are instances for which \emph{every} algorithm takes superpolynomial time, even though \emph{unconditional} sampling is provably fast. We also show that the exponential-time rejection sampling algorithm is essentially optimal under the stronger plausible assumption that there are one-way functions that take exponential time to invert.

PerMod: Perceptually Grounded Voice Modification with Latent Diffusion Models

Perceptual modification of voice is an elusive goal. While non-experts can modify an image or sentence perceptually with available tools, it is not clear how to similarly modify speech along perceptual axes. Voice conversion does make it possible to convert one voice to another, but these modifications are handled by black box models, and the specifics of what perceptual qualities to modify and how to modify them are unclear. Towards allowing greater perceptual control over voice, we introduce PerMod, a conditional latent diffusion model that takes in an input voice and a perceptual qualities vector, and produces a voice with the matching perceptual qualities. Unlike prior work, PerMod generates a new voice corresponding to specific perceptual modifications. Evaluating perceptual quality vectors with RMSE from both human and predicted labels, we demonstrate that PerMod produces voices with the desired perceptual qualities for typical voices, but performs poorly on atypical voices.

Optimizing Sampling Patterns for Compressed Sensing MRI with Diffusion Generative Models

Diffusion-based generative models have been used as powerful priors for magnetic resonance imaging (MRI) reconstruction. We present a learning method to optimize sub-sampling patterns for compressed sensing multi-coil MRI that leverages pre-trained diffusion generative models. Crucially, during training we use a single-step reconstruction based on the posterior mean estimate given by the diffusion model and the MRI measurement process. Experiments across varying anatomies, acceleration factors, and pattern types show that sampling operators learned with our method lead to competitive, and in the case of 2D patterns, improved reconstructions compared to baseline patterns. Our method requires as few as five training images to learn effective sampling patterns.

Conditional Score-Based Reconstructions for Multi-contrast MRI

Magnetic resonance imaging (MRI) exam protocols consist of multiple contrast-weighted images of the same anatomy to emphasize different tissue properties. Due to the long acquisition times required to collect fully sampled k-space measurements, it is common to only collect a fraction of k-space for some, or all, of the scans and subsequently solve an inverse problem for each contrast to recover the desired image from sub-sampled measurements. Recently, there has been a push to further accelerate MRI exams using data-driven priors, and generative models in particular, to regularize the ill-posed inverse problem of image reconstruction. These methods have shown promising improvements over classical methods. However, many of the approaches neglect the multi-contrast nature of clinical MRI exams and treat each scan as an independent reconstruction. In this work we show that by learning a joint Bayesian prior over multi-contrast data with a score-based generative model we are able to leverage the underlying structure between multi-contrast images and thus improve image reconstruction fidelity over generative models that only reconstruct images of a single contrast.

Accelerated Motion Correction for MRI using Score-Based Generative Models

Magnetic Resonance Imaging (MRI) is a powerful medical imaging modality, but unfortunately suffers from long scan times which, aside from increasing operational costs, can lead to image artifacts due to patient motion. Motion during the acquisition leads to inconsistencies in measured data that manifest as blurring and ghosting if unaccounted for in the image reconstruction process. Various deep learning based reconstruction techniques have been proposed which decrease scan time by reducing the number of measurements needed for a high fidelity reconstructed image. Additionally, deep learning has been used to correct motion using end-to-end techniques. This, however, increases susceptibility to distribution shifts at test time (sampling pattern, motion level). In this work we propose a framework for jointly reconstructing highly sub-sampled MRI data while estimating patient motion using score-based generative models. Our method does not make specific assumptions on the sampling trajectory or motion pattern at training time and thus can be flexibly applied to various types of measurement models and patient motion. We demonstrate our framework on retrospectively accelerated 2D brain MRI corrupted by rigid motion.

Robust Compressed Sensing MRI with Deep Generative Priors

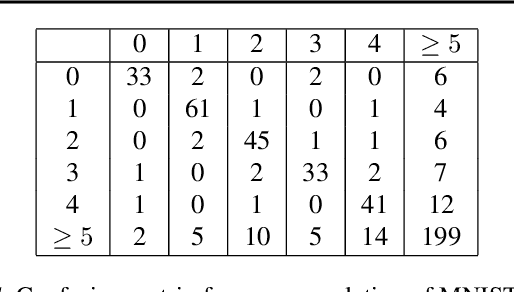
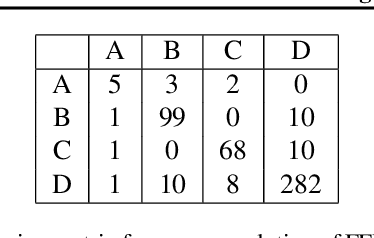
The CSGM framework (Bora-Jalal-Price-Dimakis'17) has shown that deep generative priors can be powerful tools for solving inverse problems. However, to date this framework has been empirically successful only on certain datasets (for example, human faces and MNIST digits), and it is known to perform poorly on out-of-distribution samples. In this paper, we present the first successful application of the CSGM framework on clinical MRI data. We train a generative prior on brain scans from the fastMRI dataset, and show that posterior sampling via Langevin dynamics achieves high quality reconstructions. Furthermore, our experiments and theory show that posterior sampling is robust to changes in the ground-truth distribution and measurement process. Our code and models are available at: \url{https://github.com/utcsilab/csgm-mri-langevin}.

Fairness for Image Generation with Uncertain Sensitive Attributes

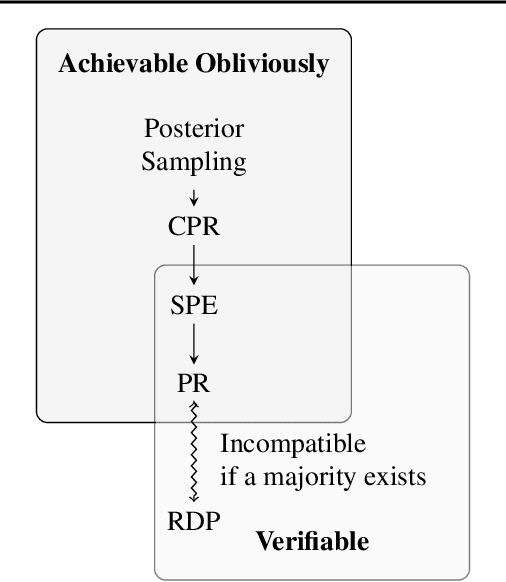
This work tackles the issue of fairness in the context of generative procedures, such as image super-resolution, which entail different definitions from the standard classification setting. Moreover, while traditional group fairness definitions are typically defined with respect to specified protected groups -- camouflaging the fact that these groupings are artificial and carry historical and political motivations -- we emphasize that there are no ground truth identities. For instance, should South and East Asians be viewed as a single group or separate groups? Should we consider one race as a whole or further split by gender? Choosing which groups are valid and who belongs in them is an impossible dilemma and being "fair" with respect to Asians may require being "unfair" with respect to South Asians. This motivates the introduction of definitions that allow algorithms to be \emph{oblivious} to the relevant groupings. We define several intuitive notions of group fairness and study their incompatibilities and trade-offs. We show that the natural extension of demographic parity is strongly dependent on the grouping, and \emph{impossible} to achieve obliviously. On the other hand, the conceptually new definition we introduce, Conditional Proportional Representation, can be achieved obliviously through Posterior Sampling. Our experiments validate our theoretical results and achieve fair image reconstruction using state-of-the-art generative models.

Instance-Optimal Compressed Sensing via Posterior Sampling

We characterize the measurement complexity of compressed sensing of signals drawn from a known prior distribution, even when the support of the prior is the entire space (rather than, say, sparse vectors). We show for Gaussian measurements and \emph{any} prior distribution on the signal, that the posterior sampling estimator achieves near-optimal recovery guarantees. Moreover, this result is robust to model mismatch, as long as the distribution estimate (e.g., from an invertible generative model) is close to the true distribution in Wasserstein distance. We implement the posterior sampling estimator for deep generative priors using Langevin dynamics, and empirically find that it produces accurate estimates with more diversity than MAP.

Intermediate Layer Optimization for Inverse Problems using Deep Generative Models

We propose Intermediate Layer Optimization (ILO), a novel optimization algorithm for solving inverse problems with deep generative models. Instead of optimizing only over the initial latent code, we progressively change the input layer obtaining successively more expressive generators. To explore the higher dimensional spaces, our method searches for latent codes that lie within a small $l_1$ ball around the manifold induced by the previous layer. Our theoretical analysis shows that by keeping the radius of the ball relatively small, we can improve the established error bound for compressed sensing with deep generative models. We empirically show that our approach outperforms state-of-the-art methods introduced in StyleGAN-2 and PULSE for a wide range of inverse problems including inpainting, denoising, super-resolution and compressed sensing.