Advancing Enterprise Spatio-Temporal Forecasting Applications: Data Mining Meets Instruction Tuning of Language Models For Multi-modal Time Series Analysis in Low-Resource Settings

Spatio-temporal forecasting is crucial in transportation, logistics, and supply chain management. However, current methods struggle with large, complex datasets. We propose a dynamic, multi-modal approach that integrates the strengths of traditional forecasting methods and instruction tuning of small language models for time series trend analysis. This approach utilizes a mixture of experts (MoE) architecture with parameter-efficient fine-tuning (PEFT) methods, tailored for consumer hardware to scale up AI solutions in low resource settings while balancing performance and latency tradeoffs. Additionally, our approach leverages related past experiences for similar input time series to efficiently handle both intra-series and inter-series dependencies of non-stationary data with a time-then-space modeling approach, using grouped-query attention, while mitigating the limitations of traditional forecasting techniques in handling distributional shifts. Our approach models predictive uncertainty to improve decision-making. Our framework enables on-premises customization with reduced computational and memory demands, while maintaining inference speed and data privacy/security. Extensive experiments on various real-world datasets demonstrate that our framework provides robust and accurate forecasts, significantly outperforming existing methods.

Joint Hypergraph Rewiring and Memory-Augmented Forecasting Techniques in Digital Twin Technology

Digital Twin technology creates virtual replicas of physical objects, processes, or systems by replicating their properties, data, and behaviors. This advanced technology offers a range of intelligent functionalities, such as modeling, simulation, and data-driven decision-making, that facilitate design optimization, performance estimation, and monitoring operations. Forecasting plays a pivotal role in Digital Twin technology, as it enables the prediction of future outcomes, supports informed decision-making, minimizes risks, driving improvements in efficiency, productivity, and cost reduction. Recently, Digital Twin technology has leveraged Graph forecasting techniques in large-scale complex sensor networks to enable accurate forecasting and simulation of diverse scenarios, fostering proactive and data-driven decision making. However, existing Graph forecasting techniques lack scalability for many real-world applications. They have limited ability to adapt to non-stationary environments, retain past knowledge, lack a mechanism to capture the higher order spatio-temporal dynamics, and estimate uncertainty in model predictions. To surmount the challenges, we introduce a hybrid architecture that enhances the hypergraph representation learning backbone by incorporating fast adaptation to new patterns and memory-based retrieval of past knowledge. This balance aims to improve the slowly-learned backbone and achieve better performance in adapting to recent changes. In addition, it models the time-varying uncertainty of multi-horizon forecasts, providing estimates of prediction uncertainty. Our forecasting architecture has been validated through ablation studies and has demonstrated promising results across multiple benchmark datasets, surpassing state-ofthe-art forecasting methods by a significant margin.

Multi-Source Knowledge-Based Hybrid Neural Framework for Time Series Representation Learning

Accurately predicting the behavior of complex dynamical systems, characterized by high-dimensional multivariate time series(MTS) in interconnected sensor networks, is crucial for informed decision-making in various applications to minimize risk. While graph forecasting networks(GFNs) are ideal for forecasting MTS data that exhibit spatio-temporal dependencies, prior works rely solely on the domain-specific knowledge of time-series variables inter-relationships to model the nonlinear dynamics, neglecting inherent relational structural dependencies among the variables within the MTS data. In contrast, contemporary works infer relational structures from MTS data but neglect domain-specific knowledge. The proposed hybrid architecture addresses these limitations by combining both domain-specific knowledge and implicit knowledge of the relational structure underlying the MTS data using Knowledge-Based Compositional Generalization. The hybrid architecture shows promising results on multiple benchmark datasets, outperforming state-of-the-art forecasting methods. Additionally, the architecture models the time varying uncertainty of multi-horizon forecasts.

Multi-Knowledge Fusion Network for Time Series Representation Learning

Forecasting the behaviour of complex dynamical systems such as interconnected sensor networks characterized by high-dimensional multivariate time series(MTS) is of paramount importance for making informed decisions and planning for the future in a broad spectrum of applications. Graph forecasting networks(GFNs) are well-suited for forecasting MTS data that exhibit spatio-temporal dependencies. However, most prior works of GFN-based methods on MTS forecasting rely on domain-expertise to model the nonlinear dynamics of the system, but neglect the potential to leverage the inherent relational-structural dependencies among time series variables underlying MTS data. On the other hand, contemporary works attempt to infer the relational structure of the complex dependencies between the variables and simultaneously learn the nonlinear dynamics of the interconnected system but neglect the possibility of incorporating domain-specific prior knowledge to improve forecast accuracy. To this end, we propose a hybrid architecture that combines explicit prior knowledge with implicit knowledge of the relational structure within the MTS data. It jointly learns intra-series temporal dependencies and inter-series spatial dependencies by encoding time-conditioned structural spatio-temporal inductive biases to provide more accurate and reliable forecasts. It also models the time-varying uncertainty of the multi-horizon forecasts to support decision-making by providing estimates of prediction uncertainty. The proposed architecture has shown promising results on multiple benchmark datasets and outperforms state-of-the-art forecasting methods by a significant margin. We report and discuss the ablation studies to validate our forecasting architecture.

PointSAGE: Mesh-independent superresolution approach to fluid flow predictions

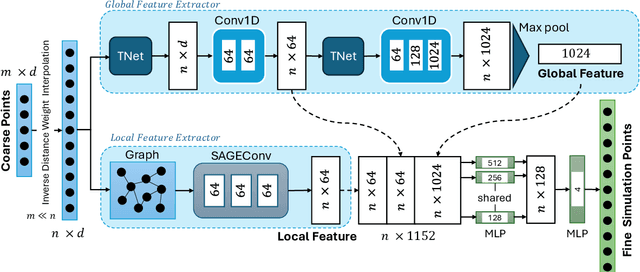
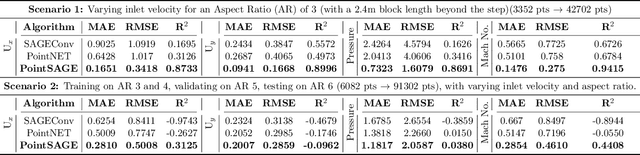
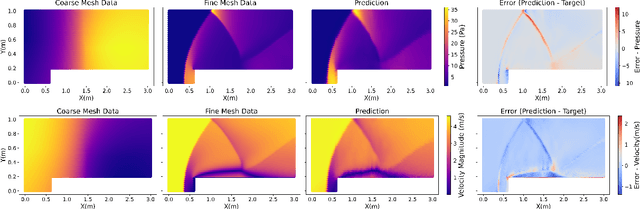
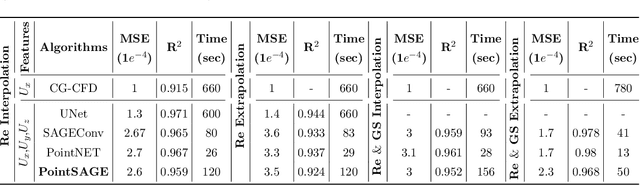
Computational Fluid Dynamics (CFD) serves as a powerful tool for simulating fluid flow across diverse industries. High-resolution CFD simulations offer valuable insights into fluid behavior and flow patterns, aiding in optimizing design features or enhancing system performance. However, as resolution increases, computational data requirements and time increase proportionately. This presents a persistent challenge in CFD. Recently, efforts have been directed towards accurately predicting fine-mesh simulations using coarse-mesh simulations, with geometry and boundary conditions as input. Drawing inspiration from models designed for super-resolution, deep learning techniques like UNets have been applied to address this challenge. However, these existing methods are limited to structured data and fail if the mesh is unstructured due to its inability to convolute. Additionally, incorporating geometry/mesh information in the training process introduces drawbacks such as increased data requirements, challenges in generalizing to unseen geometries for the same physical phenomena, and issues with robustness to mesh distortions. To address these concerns, we propose a novel framework, PointSAGE a mesh-independent network that leverages the unordered, mesh-less nature of Pointcloud to learn the complex fluid flow and directly predict fine simulations, completely neglecting mesh information. Utilizing an adaptable framework, the model accurately predicts the fine data across diverse point cloud sizes, regardless of the training dataset's dimension. We have evaluated the effectiveness of PointSAGE on diverse datasets in different scenarios, demonstrating notable results and a significant acceleration in computational time in generating fine simulations compared to standard CFD techniques.

Redefining Super-Resolution: Fine-mesh PDE predictions without classical simulations

In Computational Fluid Dynamics (CFD), coarse mesh simulations offer computational efficiency but often lack precision. Applying conventional super-resolution to these simulations poses a significant challenge due to the fundamental contrast between downsampling high-resolution images and authentically emulating low-resolution physics. The former method conserves more of the underlying physics, surpassing the usual constraints of real-world scenarios. We propose a novel definition of super-resolution tailored for PDE-based problems. Instead of simply downsampling from a high-resolution dataset, we use coarse-grid simulated data as our input and predict fine-grid simulated outcomes. Employing a physics-infused UNet upscaling method, we demonstrate its efficacy across various 2D-CFD problems such as discontinuity detection in Burger's equation, Methane combustion, and fouling in Industrial heat exchangers. Our method enables the generation of fine-mesh solutions bypassing traditional simulation, ensuring considerable computational saving and fidelity to the original ground truth outcomes. Through diverse boundary conditions during training, we further establish the robustness of our method, paving the way for its broad applications in engineering and scientific CFD solvers.