Concept-driven Off Policy Evaluation

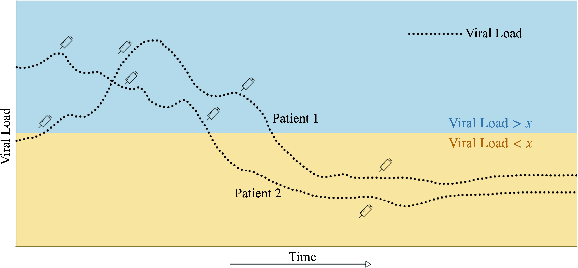
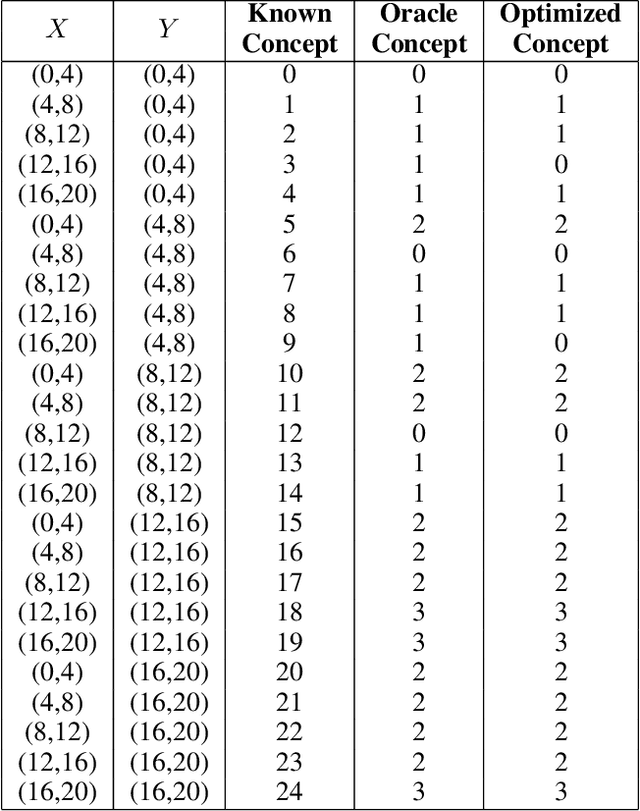
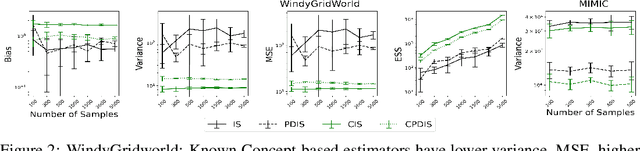
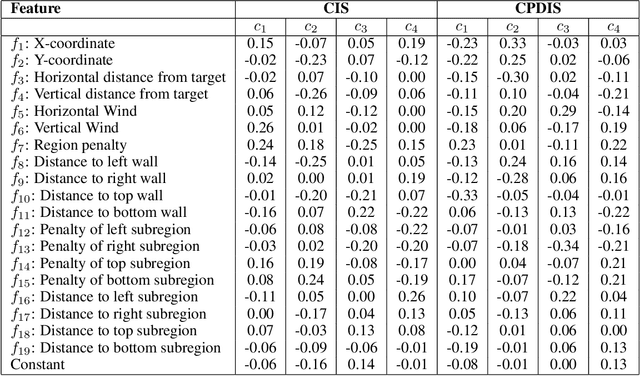
Evaluating off-policy decisions using batch data poses significant challenges due to limited sample sizes leading to high variance. To improve Off-Policy Evaluation (OPE), we must identify and address the sources of this variance. Recent research on Concept Bottleneck Models (CBMs) shows that using human-explainable concepts can improve predictions and provide better understanding. We propose incorporating concepts into OPE to reduce variance. Our work introduces a family of concept-based OPE estimators, proving that they remain unbiased and reduce variance when concepts are known and predefined. Since real-world applications often lack predefined concepts, we further develop an end-to-end algorithm to learn interpretable, concise, and diverse parameterized concepts optimized for variance reduction. Our experiments with synthetic and real-world datasets show that both known and learned concept-based estimators significantly improve OPE performance. Crucially, we show that, unlike other OPE methods, concept-based estimators are easily interpretable and allow for targeted interventions on specific concepts, further enhancing the quality of these estimators.

Redefining Super-Resolution: Fine-mesh PDE predictions without classical simulations

In Computational Fluid Dynamics (CFD), coarse mesh simulations offer computational efficiency but often lack precision. Applying conventional super-resolution to these simulations poses a significant challenge due to the fundamental contrast between downsampling high-resolution images and authentically emulating low-resolution physics. The former method conserves more of the underlying physics, surpassing the usual constraints of real-world scenarios. We propose a novel definition of super-resolution tailored for PDE-based problems. Instead of simply downsampling from a high-resolution dataset, we use coarse-grid simulated data as our input and predict fine-grid simulated outcomes. Employing a physics-infused UNet upscaling method, we demonstrate its efficacy across various 2D-CFD problems such as discontinuity detection in Burger's equation, Methane combustion, and fouling in Industrial heat exchangers. Our method enables the generation of fine-mesh solutions bypassing traditional simulation, ensuring considerable computational saving and fidelity to the original ground truth outcomes. Through diverse boundary conditions during training, we further establish the robustness of our method, paving the way for its broad applications in engineering and scientific CFD solvers.

Can Physics Informed Neural Operators Self Improve?

Self-training techniques have shown remarkable value across many deep learning models and tasks. However, such techniques remain largely unexplored when considered in the context of learning fast solvers for systems of partial differential equations (Eg: Neural Operators). In this work, we explore the use of self-training for Fourier Neural Operators (FNO). Neural Operators emerged as a data driven technique, however, data from experiments or traditional solvers is not always readily available. Physics Informed Neural Operators (PINO) overcome this constraint by utilizing a physics loss for the training, however the accuracy of PINO trained without data does not match the performance obtained by training with data. In this work we show that self-training can be used to close this gap in performance. We examine canonical examples, namely the 1D-Burgers and 2D-Darcy PDEs, to showcase the efficacy of self-training. Specifically, FNOs, when trained exclusively with physics loss through self-training, approach 1.07x for Burgers and 1.02x for Darcy, compared to FNOs trained with both data and physics loss. Furthermore, we discover that pseudo-labels can be used for self-training without necessarily training to convergence in each iteration. A consequence of this is that we are able to discover self-training schedules that improve upon the baseline performance of PINO in terms of accuracy as well as time.

HyperLoRA for PDEs

Physics-informed neural networks (PINNs) have been widely used to develop neural surrogates for solutions of Partial Differential Equations. A drawback of PINNs is that they have to be retrained with every change in initial-boundary conditions and PDE coefficients. The Hypernetwork, a model-based meta learning technique, takes in a parameterized task embedding as input and predicts the weights of PINN as output. Predicting weights of a neural network however, is a high-dimensional regression problem, and hypernetworks perform sub-optimally while predicting parameters for large base networks. To circumvent this issue, we use a low ranked adaptation (LoRA) formulation to decompose every layer of the base network into low-ranked tensors and use hypernetworks to predict the low-ranked tensors. Despite the reduced dimensionality of the resulting weight-regression problem, LoRA-based Hypernetworks violate the underlying physics of the given task. We demonstrate that the generalization capabilities of LoRA-based hypernetworks drastically improve when trained with an additional physics-informed loss component (HyperPINN) to satisfy the governing differential equations. We observe that LoRA-based HyperPINN training allows us to learn fast solutions for parameterized PDEs like Burger's equation and Navier Stokes: Kovasznay flow, while having an 8x reduction in prediction parameters on average without compromising on accuracy when compared to all other baselines.

How important are specialized transforms in Neural Operators?

Simulating physical systems using Partial Differential Equations (PDEs) has become an indispensible part of modern industrial process optimization. Traditionally, numerical solvers have been used to solve the associated PDEs, however recently Transform-based Neural Operators such as the Fourier Neural Operator and Wavelet Neural Operator have received a lot of attention for their potential to provide fast solutions for systems of PDEs. In this work, we investigate the importance of the transform layers to the reported success of transform based neural operators. In particular, we record the cost in terms of performance, if all the transform layers are replaced by learnable linear layers. Surprisingly, we observe that linear layers suffice to provide performance comparable to the best-known transform-based layers and seem to do so with a compute time advantage as well. We believe that this observation can have significant implications for future work on Neural Operators, and might point to other sources of efficiencies for these architectures.

DeepEpiSolver: Unravelling Inverse problems in Covid, HIV, Ebola and Disease Transmission

The spread of many infectious diseases is modeled using variants of the SIR compartmental model, which is a coupled differential equation. The coefficients of the SIR model determine the spread trajectories of disease, on whose basis proactive measures can be taken. Hence, the coefficient estimates must be both fast and accurate. Shaier et al. in the paper "Disease Informed Neural Networks" used Physics Informed Neural Networks (PINNs) to estimate the parameters of the SIR model. There are two drawbacks to this approach. First, the training time for PINNs is high, with certain diseases taking close to 90 hrs to train. Second, PINNs don't generalize for a new SIDR trajectory, and learning its corresponding SIR parameters requires retraining the PINN from scratch. In this work, we aim to eliminate both of these drawbacks. We generate a dataset between the parameters of ODE and the spread trajectories by solving the forward problem for a large distribution of parameters using the LSODA algorithm. We then use a neural network to learn the mapping between spread trajectories and coefficients of SIDR in an offline manner. This allows us to learn the parameters of a new spread trajectory without having to retrain, enabling generalization at test time. We observe a speed-up of 3-4 orders of magnitude with accuracy comparable to that of PINNs for 11 highly infectious diseases. Further finetuning of neural network inferred ODE coefficients using PINN further leads to 2-3 orders improvement of estimated coefficients.

Symbolic Regression for PDEs using Pruned Differentiable Programs

Physics-informed Neural Networks (PINNs) have been widely used to obtain accurate neural surrogates for a system of Partial Differential Equations (PDE). One of the major limitations of PINNs is that the neural solutions are challenging to interpret, and are often treated as black-box solvers. While Symbolic Regression (SR) has been studied extensively, very few works exist which generate analytical expressions to directly perform SR for a system of PDEs. In this work, we introduce an end-to-end framework for obtaining mathematical expressions for solutions of PDEs. We use a trained PINN to generate a dataset, upon which we perform SR. We use a Differentiable Program Architecture (DPA) defined using context-free grammar to describe the space of symbolic expressions. We improve the interpretability by pruning the DPA in a depth-first manner using the magnitude of weights as our heuristic. On average, we observe a 95.3% reduction in parameters of DPA while maintaining accuracy at par with PINNs. Furthermore, on an average, pruning improves the accuracy of DPA by 7.81% . We demonstrate our framework outperforms the existing state-of-the-art SR solvers on systems of complex PDEs like Navier-Stokes: Kovasznay flow and Taylor-Green Vortex flow. Furthermore, we produce analytical expressions for a complex industrial use-case of an Air-Preheater, without suffering from performance loss viz-a-viz PINNs.

Real-time Health Monitoring of Heat Exchangers using Hypernetworks and PINNs

We demonstrate a Physics-informed Neural Network (PINN) based model for real-time health monitoring of a heat exchanger, that plays a critical role in improving energy efficiency of thermal power plants. A hypernetwork based approach is used to enable the domain-decomposed PINN learn the thermal behavior of the heat exchanger in response to dynamic boundary conditions, eliminating the need to re-train. As a result, we achieve orders of magnitude reduction in inference time in comparison to existing PINNs, while maintaining the accuracy on par with the physics-based simulations. This makes the approach very attractive for predictive maintenance of the heat exchanger in digital twin environments.

On NeuroSymbolic Solutions for PDEs

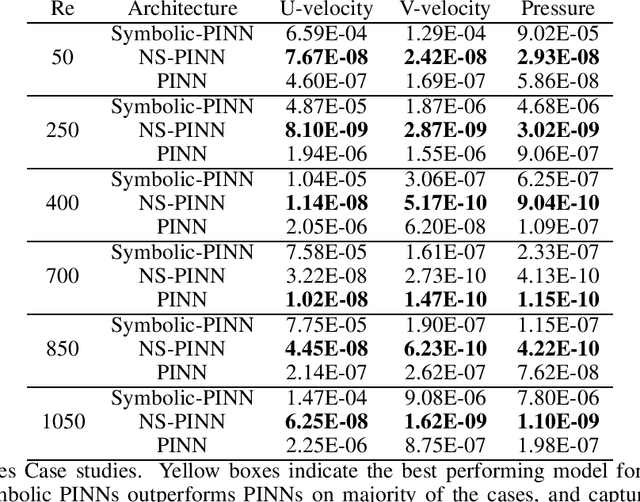
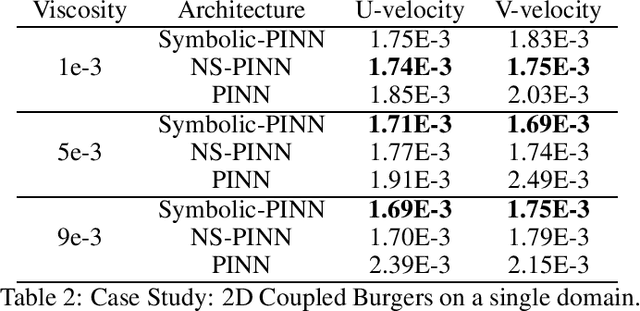
Physics Informed Neural Networks (PINNs) have gained immense popularity as an alternate method for numerically solving PDEs. Despite their empirical success we are still building an understanding of the convergence properties of training on such constraints with gradient descent. It is known that, in the absence of an explicit inductive bias, Neural Networks can struggle to learn or approximate even simple and well known functions in a sample efficient manner. Thus the numerical approximation induced from few collocation points may not generalize over the entire domain. Meanwhile, a symbolic form can exhibit good generalization, with interpretability as a useful byproduct. However, symbolic approximations can struggle to simultaneously be concise and accurate. Therefore in this work we explore a NeuroSymbolic approach to approximate the solution for PDEs. We observe that our approach work for several simple cases. We illustrate the efficacy of our approach on Navier Stokes: Kovasznay flow where there are multiple physical quantities of interest governed with non-linear coupled PDE system. Domain splitting is now becoming a popular trick to help PINNs approximate complex functions. We observe that a NeuroSymbolic approach can help such complex functions as well. We demonstrate Domain-splitting assisted NeuroSymbolic approach on a temporally varying two-dimensional Burger's equation. Finally we consider the scenario where PINNs have to be solved for parameterized PDEs, for changing Initial-Boundary Conditions and changes in the coefficient of the PDEs. Hypernetworks have shown to hold promise to overcome these challenges. We show that one can design Hyper-NeuroSymbolic Networks which can combine the benefits of speed and increased accuracy. We observe that that the NeuroSymbolic approximations are consistently 1-2 order of magnitude better than just the neural or symbolic approximations.