OrgAccess: A Benchmark for Role Based Access Control in Organization Scale LLMs

Role-based access control (RBAC) and hierarchical structures are foundational to how information flows and decisions are made within virtually all organizations. As the potential of Large Language Models (LLMs) to serve as unified knowledge repositories and intelligent assistants in enterprise settings becomes increasingly apparent, a critical, yet under explored, challenge emerges: \textit{can these models reliably understand and operate within the complex, often nuanced, constraints imposed by organizational hierarchies and associated permissions?} Evaluating this crucial capability is inherently difficult due to the proprietary and sensitive nature of real-world corporate data and access control policies. We introduce a synthetic yet representative \textbf{OrgAccess} benchmark consisting of 40 distinct types of permissions commonly relevant across different organizational roles and levels. We further create three types of permissions: 40,000 easy (1 permission), 10,000 medium (3-permissions tuple), and 20,000 hard (5-permissions tuple) to test LLMs' ability to accurately assess these permissions and generate responses that strictly adhere to the specified hierarchical rules, particularly in scenarios involving users with overlapping or conflicting permissions. Our findings reveal that even state-of-the-art LLMs struggle significantly to maintain compliance with role-based structures, even with explicit instructions, with their performance degrades further when navigating interactions involving two or more conflicting permissions. Specifically, even \textbf{GPT-4.1 only achieves an F1-Score of 0.27 on our hardest benchmark}. This demonstrates a critical limitation in LLMs' complex rule following and compositional reasoning capabilities beyond standard factual or STEM-based benchmarks, opening up a new paradigm for evaluating their fitness for practical, structured environments.

Nine Ways to Break Copyright Law and Why Our LLM Won't: A Fair Use Aligned Generation Framework

Large language models (LLMs) commonly risk copyright infringement by reproducing protected content verbatim or with insufficient transformative modifications, posing significant ethical, legal, and practical concerns. Current inference-time safeguards predominantly rely on restrictive refusal-based filters, often compromising the practical utility of these models. To address this, we collaborated closely with intellectual property experts to develop FUA-LLM (Fair Use Aligned Language Models), a legally-grounded framework explicitly designed to align LLM outputs with fair-use doctrine. Central to our method is FairUseDB, a carefully constructed dataset containing 18,000 expert-validated examples covering nine realistic infringement scenarios. Leveraging this dataset, we apply Direct Preference Optimization (DPO) to fine-tune open-source LLMs, encouraging them to produce legally compliant and practically useful alternatives rather than resorting to blunt refusal. Recognizing the shortcomings of traditional evaluation metrics, we propose new measures: Weighted Penalty Utility and Compliance Aware Harmonic Mean (CAH) to balance infringement risk against response utility. Extensive quantitative experiments coupled with expert evaluations confirm that FUA-LLM substantially reduces problematic outputs (up to 20\%) compared to state-of-the-art approaches, while preserving real-world usability.

Guardians of Generation: Dynamic Inference-Time Copyright Shielding with Adaptive Guidance for AI Image Generation

Modern text-to-image generative models can inadvertently reproduce copyrighted content memorized in their training data, raising serious concerns about potential copyright infringement. We introduce Guardians of Generation, a model agnostic inference time framework for dynamic copyright shielding in AI image generation. Our approach requires no retraining or modification of the generative model weights, instead integrating seamlessly with existing diffusion pipelines. It augments the generation process with an adaptive guidance mechanism comprising three components: a detection module, a prompt rewriting module, and a guidance adjustment module. The detection module monitors user prompts and intermediate generation steps to identify features indicative of copyrighted content before they manifest in the final output. If such content is detected, the prompt rewriting mechanism dynamically transforms the user's prompt by sanitizing or replacing references that could trigger copyrighted material while preserving the prompt's intended semantics. The adaptive guidance module adaptively steers the diffusion process away from flagged content by modulating the model's sampling trajectory. Together, these components form a robust shield that enables a tunable balance between preserving creative fidelity and ensuring copyright compliance. We validate our method on a variety of generative models such as Stable Diffusion, SDXL, and Flux, demonstrating substantial reductions in copyrighted content generation with negligible impact on output fidelity or alignment with user intent. This work provides a practical, plug-and-play safeguard for generative image models, enabling more responsible deployment under real-world copyright constraints. Source code is available at: https://respailab.github.io/gog

MRI2Speech: Speech Synthesis from Articulatory Movements Recorded by Real-time MRI

Previous real-time MRI (rtMRI)-based speech synthesis models depend heavily on noisy ground-truth speech. Applying loss directly over ground truth mel-spectrograms entangles speech content with MRI noise, resulting in poor intelligibility. We introduce a novel approach that adapts the multi-modal self-supervised AV-HuBERT model for text prediction from rtMRI and incorporates a new flow-based duration predictor for speaker-specific alignment. The predicted text and durations are then used by a speech decoder to synthesize aligned speech in any novel voice. We conduct thorough experiments on two datasets and demonstrate our method's generalization ability to unseen speakers. We assess our framework's performance by masking parts of the rtMRI video to evaluate the impact of different articulators on text prediction. Our method achieves a $15.18\%$ Word Error Rate (WER) on the USC-TIMIT MRI corpus, marking a huge improvement over the current state-of-the-art. Speech samples are available at \url{https://mri2speech.github.io/MRI2Speech/}

Advancing NAM-to-Speech Conversion with Novel Methods and the MultiNAM Dataset

Current Non-Audible Murmur (NAM)-to-speech techniques rely on voice cloning to simulate ground-truth speech from paired whispers. However, the simulated speech often lacks intelligibility and fails to generalize well across different speakers. To address this issue, we focus on learning phoneme-level alignments from paired whispers and text and employ a Text-to-Speech (TTS) system to simulate the ground-truth. To reduce dependence on whispers, we learn phoneme alignments directly from NAMs, though the quality is constrained by the available training data. To further mitigate reliance on NAM/whisper data for ground-truth simulation, we propose incorporating the lip modality to infer speech and introduce a novel diffusion-based method that leverages recent advancements in lip-to-speech technology. Additionally, we release the MultiNAM dataset with over $7.96$ hours of paired NAM, whisper, video, and text data from two speakers and benchmark all methods on this dataset. Speech samples and the dataset are available at \url{https://diff-nam.github.io/DiffNAM/}

Persuasion Games using Large Language Models

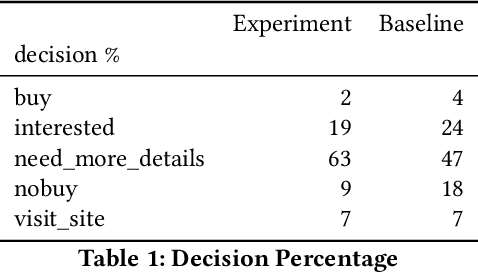
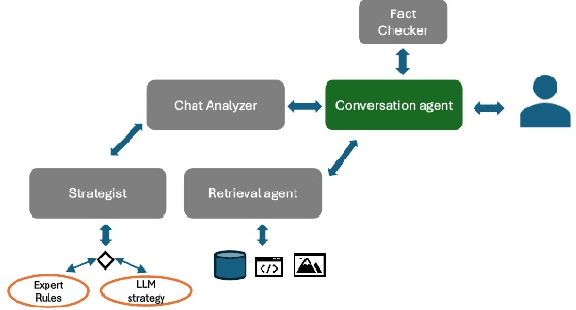
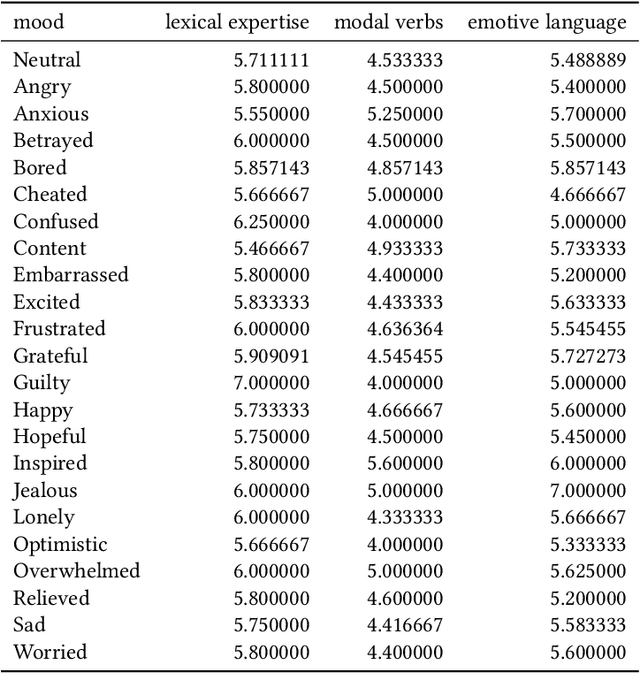
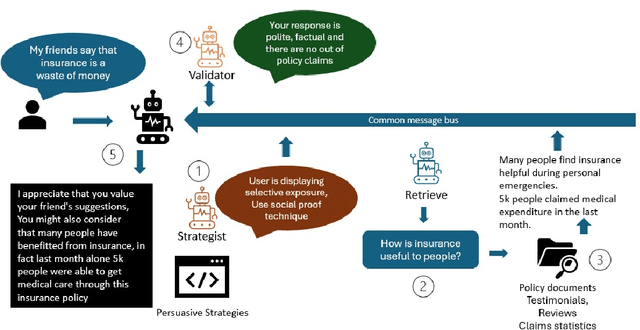
Large Language Models (LLMs) have emerged as formidable instruments capable of comprehending and producing human-like text. This paper explores the potential of LLMs, to shape user perspectives and subsequently influence their decisions on particular tasks. This capability finds applications in diverse domains such as Investment, Credit cards and Insurance, wherein they assist users in selecting appropriate insurance policies, investment plans, Credit cards, Retail, as well as in Behavioral Change Support Systems (BCSS). We present a sophisticated multi-agent framework wherein a consortium of agents operate in collaborative manner. The primary agent engages directly with user agents through persuasive dialogue, while the auxiliary agents perform tasks such as information retrieval, response analysis, development of persuasion strategies, and validation of facts. Empirical evidence from our experiments demonstrates that this collaborative methodology significantly enhances the persuasive efficacy of the LLM. We continuously analyze the resistance of the user agent to persuasive efforts and counteract it by employing a combination of rule-based and LLM-based resistance-persuasion mapping techniques. We employ simulated personas and generate conversations in insurance, banking, and retail domains to evaluate the proficiency of large language models (LLMs) in recognizing, adjusting to, and influencing various personality types. Concurrently, we examine the resistance mechanisms employed by LLM simulated personas. Persuasion is quantified via measurable surveys before and after interaction, LLM-generated scores on conversation, and user decisions (purchase or non-purchase).

Towards Improving NAM-to-Speech Synthesis Intelligibility using Self-Supervised Speech Models

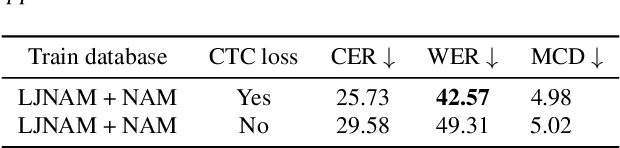
We propose a novel approach to significantly improve the intelligibility in the Non-Audible Murmur (NAM)-to-speech conversion task, leveraging self-supervision and sequence-to-sequence (Seq2Seq) learning techniques. Unlike conventional methods that explicitly record ground-truth speech, our methodology relies on self-supervision and speech-to-speech synthesis to simulate ground-truth speech. Despite utilizing simulated speech, our method surpasses the current state-of-the-art (SOTA) by 29.08% improvement in the Mel-Cepstral Distortion (MCD) metric. Additionally, we present error rates and demonstrate our model's proficiency to synthesize speech in novel voices of interest. Moreover, we present a methodology for augmenting the existing CSTR NAM TIMIT Plus corpus, setting a benchmark with a Word Error Rate (WER) of 42.57% to gauge the intelligibility of the synthesized speech. Speech samples can be found at https://nam2speech.github.io/NAM2Speech/

Towards Mitigating Perceived Unfairness in Contracts from a Non-Legal Stakeholder's Perspective

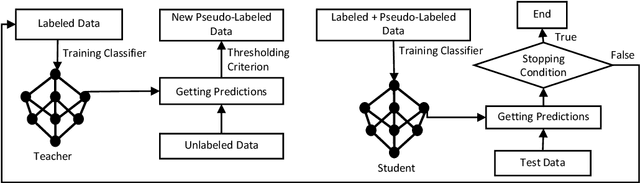
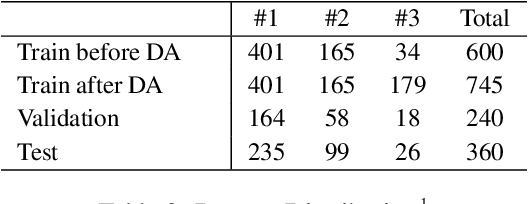
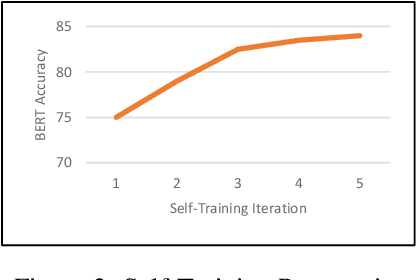
Commercial contracts are known to be a valuable source for deriving project-specific requirements. However, contract negotiations mainly occur among the legal counsel of the parties involved. The participation of non-legal stakeholders, including requirement analysts, engineers, and solution architects, whose primary responsibility lies in ensuring the seamless implementation of contractual terms, is often indirect and inadequate. Consequently, a significant number of sentences in contractual clauses, though legally accurate, can appear unfair from an implementation perspective to non-legal stakeholders. This perception poses a problem since requirements indicated in the clauses are obligatory and can involve punitive measures and penalties if not implemented as committed in the contract. Therefore, the identification of potentially unfair clauses in contracts becomes crucial. In this work, we conduct an empirical study to analyze the perspectives of different stakeholders regarding contractual fairness. We then investigate the ability of Pre-trained Language Models (PLMs) to identify unfairness in contractual sentences by comparing chain of thought prompting and semi-supervised fine-tuning approaches. Using BERT-based fine-tuning, we achieved an accuracy of 84% on a dataset consisting of proprietary contracts. It outperformed chain of thought prompting using Vicuna-13B by a margin of 9%.

Can Physics Informed Neural Operators Self Improve?

Self-training techniques have shown remarkable value across many deep learning models and tasks. However, such techniques remain largely unexplored when considered in the context of learning fast solvers for systems of partial differential equations (Eg: Neural Operators). In this work, we explore the use of self-training for Fourier Neural Operators (FNO). Neural Operators emerged as a data driven technique, however, data from experiments or traditional solvers is not always readily available. Physics Informed Neural Operators (PINO) overcome this constraint by utilizing a physics loss for the training, however the accuracy of PINO trained without data does not match the performance obtained by training with data. In this work we show that self-training can be used to close this gap in performance. We examine canonical examples, namely the 1D-Burgers and 2D-Darcy PDEs, to showcase the efficacy of self-training. Specifically, FNOs, when trained exclusively with physics loss through self-training, approach 1.07x for Burgers and 1.02x for Darcy, compared to FNOs trained with both data and physics loss. Furthermore, we discover that pseudo-labels can be used for self-training without necessarily training to convergence in each iteration. A consequence of this is that we are able to discover self-training schedules that improve upon the baseline performance of PINO in terms of accuracy as well as time.

HyperLoRA for PDEs

Physics-informed neural networks (PINNs) have been widely used to develop neural surrogates for solutions of Partial Differential Equations. A drawback of PINNs is that they have to be retrained with every change in initial-boundary conditions and PDE coefficients. The Hypernetwork, a model-based meta learning technique, takes in a parameterized task embedding as input and predicts the weights of PINN as output. Predicting weights of a neural network however, is a high-dimensional regression problem, and hypernetworks perform sub-optimally while predicting parameters for large base networks. To circumvent this issue, we use a low ranked adaptation (LoRA) formulation to decompose every layer of the base network into low-ranked tensors and use hypernetworks to predict the low-ranked tensors. Despite the reduced dimensionality of the resulting weight-regression problem, LoRA-based Hypernetworks violate the underlying physics of the given task. We demonstrate that the generalization capabilities of LoRA-based hypernetworks drastically improve when trained with an additional physics-informed loss component (HyperPINN) to satisfy the governing differential equations. We observe that LoRA-based HyperPINN training allows us to learn fast solutions for parameterized PDEs like Burger's equation and Navier Stokes: Kovasznay flow, while having an 8x reduction in prediction parameters on average without compromising on accuracy when compared to all other baselines.