A Multi-Objective Genetic Algorithm for Healthcare Workforce Scheduling

Workforce scheduling in the healthcare sector is a significant operational challenge, characterized by fluctuating patient loads, diverse clinical skills, and the critical need to control labor costs while upholding high standards of patient care. This problem is inherently multi-objective, demanding a delicate balance between competing goals: minimizing payroll, ensuring adequate staffing for patient needs, and accommodating staff preferences to mitigate burnout. We propose a Multi-objective Genetic Algorithm (MOO-GA) that models the hospital unit workforce scheduling problem as a multi-objective optimization task. Our model incorporates real-world complexities, including hourly appointment-driven demand and the use of modular shifts for a multi-skilled workforce. By defining objective functions for cost, patient care coverage, and staff satisfaction, the GA navigates the vast search space to identify a set of high-quality, non-dominated solutions. Demonstrated on datasets representing a typical hospital unit, the results show that our MOO-GA generates robust and balanced schedules. On average, the schedules produced by our algorithm showed a 66\% performance improvement over a baseline that simulates a conventional, manual scheduling process. This approach effectively manages trade-offs between critical operational and staff-centric objectives, providing a practical decision support tool for nurse managers and hospital administrators.

DETNO: A Diffusion-Enhanced Transformer Neural Operator for Long-Term Traffic Forecasting

Accurate long-term traffic forecasting remains a critical challenge in intelligent transportation systems, particularly when predicting high-frequency traffic phenomena such as shock waves and congestion boundaries over extended rollout horizons. Neural operators have recently gained attention as promising tools for modeling traffic flow. While effective at learning function space mappings, they inherently produce smooth predictions that fail to reconstruct high-frequency features such as sharp density gradients which results in rapid error accumulation during multi-step rollout predictions essential for real-time traffic management. To address these fundamental limitations, we introduce a unified Diffusion-Enhanced Transformer Neural Operator (DETNO) architecture. DETNO leverages a transformer neural operator with cross-attention mechanisms, providing model expressivity and super-resolution, coupled with a diffusion-based refinement component that iteratively reconstructs high-frequency traffic details through progressive denoising. This overcomes the inherent smoothing limitations and rollout instability of standard neural operators. Through comprehensive evaluation on chaotic traffic datasets, our method demonstrates superior performance in extended rollout predictions compared to traditional and transformer-based neural operators, preserving high-frequency components and improving stability over long prediction horizons.

Leveraging Knowledge Graphs and LLM Reasoning to Identify Operational Bottlenecks for Warehouse Planning Assistance

Analyzing large, complex output datasets from Discrete Event Simulations (DES) of warehouse operations to identify bottlenecks and inefficiencies is a critical yet challenging task, often demanding significant manual effort or specialized analytical tools. Our framework integrates Knowledge Graphs (KGs) and Large Language Model (LLM)-based agents to analyze complex Discrete Event Simulation (DES) output data from warehouse operations. It transforms raw DES data into a semantically rich KG, capturing relationships between simulation events and entities. An LLM-based agent uses iterative reasoning, generating interdependent sub-questions. For each sub-question, it creates Cypher queries for KG interaction, extracts information, and self-reflects to correct errors. This adaptive, iterative, and self-correcting process identifies operational issues mimicking human analysis. Our DES approach for warehouse bottleneck identification, tested with equipment breakdowns and process irregularities, outperforms baseline methods. For operational questions, it achieves near-perfect pass rates in pinpointing inefficiencies. For complex investigative questions, we demonstrate its superior diagnostic ability to uncover subtle, interconnected issues. This work bridges simulation modeling and AI (KG+LLM), offering a more intuitive method for actionable insights, reducing time-to-insight, and enabling automated warehouse inefficiency evaluation and diagnosis.

Accelerated Gradient-based Design Optimization Via Differentiable Physics-Informed Neural Operator: A Composites Autoclave Processing Case Study

Simulation and optimization are crucial for advancing the engineering design of complex systems and processes. Traditional optimization methods require substantial computational time and effort due to their reliance on resource-intensive simulations, such as finite element analysis, and the complexity of rigorous optimization algorithms. Data-agnostic AI-based surrogate models, such as Physics-Informed Neural Operators (PINOs), offer a promising alternative to these conventional simulations, providing drastically reduced inference time, unparalleled data efficiency, and zero-shot super-resolution capability. However, the predictive accuracy of these models is often constrained to small, low-dimensional design spaces or systems with relatively simple dynamics. To address this, we introduce a novel Physics-Informed DeepONet (PIDON) architecture, which extends the capabilities of conventional neural operators to effectively model the nonlinear behavior of complex engineering systems across high-dimensional design spaces and a wide range of dynamic design configurations. This new architecture outperforms existing SOTA models, enabling better predictions across broader design spaces. Leveraging PIDON's differentiability, we integrate a gradient-based optimization approach using the Adam optimizer to efficiently determine optimal design variables. This forms an end-to-end gradient-based optimization framework that accelerates the design process while enhancing scalability and efficiency. We demonstrate the effectiveness of this framework in the optimization of aerospace-grade composites curing processes achieving a 3x speedup in obtaining optimal design variables compared to gradient-free methods. Beyond composites processing, the proposed model has the potential to be used as a scalable and efficient optimization tool for broader applications in advanced engineering and digital twin systems.

FB-HyDON: Parameter-Efficient Physics-Informed Operator Learning of Complex PDEs via Hypernetwork and Finite Basis Domain Decomposition

Deep operator networks (DeepONet) and neural operators have gained significant attention for their ability to map infinite-dimensional function spaces and perform zero-shot super-resolution. However, these models often require large datasets for effective training. While physics-informed operators offer a data-agnostic learning approach, they introduce additional training complexities and convergence issues, especially in highly nonlinear systems. To overcome these challenges, we introduce Finite Basis Physics-Informed HyperDeepONet (FB-HyDON), an advanced operator architecture featuring intrinsic domain decomposition. By leveraging hypernetworks and finite basis functions, FB-HyDON effectively mitigates the training limitations associated with existing physics-informed operator learning methods. We validated our approach on the high-frequency harmonic oscillator, Burgers' equation at different viscosity levels, and Allen-Cahn equation demonstrating substantial improvements over other operator learning models.

An Advanced Physics-Informed Neural Operator for Comprehensive Design Optimization of Highly-Nonlinear Systems: An Aerospace Composites Processing Case Study

Deep Operator Networks (DeepONets) and their physics-informed variants have shown significant promise in learning mappings between function spaces of partial differential equations, enhancing the generalization of traditional neural networks. However, for highly nonlinear real-world applications like aerospace composites processing, existing models often fail to capture underlying solutions accurately and are typically limited to single input functions, constraining rapid process design development. This paper introduces an advanced physics-informed DeepONet tailored for such complex systems with multiple input functions. Equipped with architectural enhancements like nonlinear decoders and effective training strategies such as curriculum learning and domain decomposition, the proposed model handles high-dimensional design spaces with significantly improved accuracy, outperforming the vanilla physics-informed DeepONet by two orders of magnitude. Its zero-shot prediction capability across a broad design space makes it a powerful tool for accelerating composites process design and optimization, with potential applications in other engineering fields characterized by strong nonlinearity.

HyperLoRA for PDEs

Physics-informed neural networks (PINNs) have been widely used to develop neural surrogates for solutions of Partial Differential Equations. A drawback of PINNs is that they have to be retrained with every change in initial-boundary conditions and PDE coefficients. The Hypernetwork, a model-based meta learning technique, takes in a parameterized task embedding as input and predicts the weights of PINN as output. Predicting weights of a neural network however, is a high-dimensional regression problem, and hypernetworks perform sub-optimally while predicting parameters for large base networks. To circumvent this issue, we use a low ranked adaptation (LoRA) formulation to decompose every layer of the base network into low-ranked tensors and use hypernetworks to predict the low-ranked tensors. Despite the reduced dimensionality of the resulting weight-regression problem, LoRA-based Hypernetworks violate the underlying physics of the given task. We demonstrate that the generalization capabilities of LoRA-based hypernetworks drastically improve when trained with an additional physics-informed loss component (HyperPINN) to satisfy the governing differential equations. We observe that LoRA-based HyperPINN training allows us to learn fast solutions for parameterized PDEs like Burger's equation and Navier Stokes: Kovasznay flow, while having an 8x reduction in prediction parameters on average without compromising on accuracy when compared to all other baselines.

Symbolic Regression for PDEs using Pruned Differentiable Programs

Physics-informed Neural Networks (PINNs) have been widely used to obtain accurate neural surrogates for a system of Partial Differential Equations (PDE). One of the major limitations of PINNs is that the neural solutions are challenging to interpret, and are often treated as black-box solvers. While Symbolic Regression (SR) has been studied extensively, very few works exist which generate analytical expressions to directly perform SR for a system of PDEs. In this work, we introduce an end-to-end framework for obtaining mathematical expressions for solutions of PDEs. We use a trained PINN to generate a dataset, upon which we perform SR. We use a Differentiable Program Architecture (DPA) defined using context-free grammar to describe the space of symbolic expressions. We improve the interpretability by pruning the DPA in a depth-first manner using the magnitude of weights as our heuristic. On average, we observe a 95.3% reduction in parameters of DPA while maintaining accuracy at par with PINNs. Furthermore, on an average, pruning improves the accuracy of DPA by 7.81% . We demonstrate our framework outperforms the existing state-of-the-art SR solvers on systems of complex PDEs like Navier-Stokes: Kovasznay flow and Taylor-Green Vortex flow. Furthermore, we produce analytical expressions for a complex industrial use-case of an Air-Preheater, without suffering from performance loss viz-a-viz PINNs.

Real-time Health Monitoring of Heat Exchangers using Hypernetworks and PINNs

We demonstrate a Physics-informed Neural Network (PINN) based model for real-time health monitoring of a heat exchanger, that plays a critical role in improving energy efficiency of thermal power plants. A hypernetwork based approach is used to enable the domain-decomposed PINN learn the thermal behavior of the heat exchanger in response to dynamic boundary conditions, eliminating the need to re-train. As a result, we achieve orders of magnitude reduction in inference time in comparison to existing PINNs, while maintaining the accuracy on par with the physics-based simulations. This makes the approach very attractive for predictive maintenance of the heat exchanger in digital twin environments.

On NeuroSymbolic Solutions for PDEs

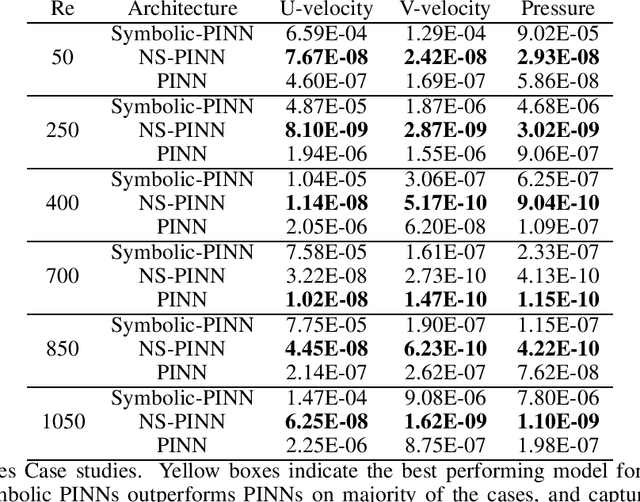
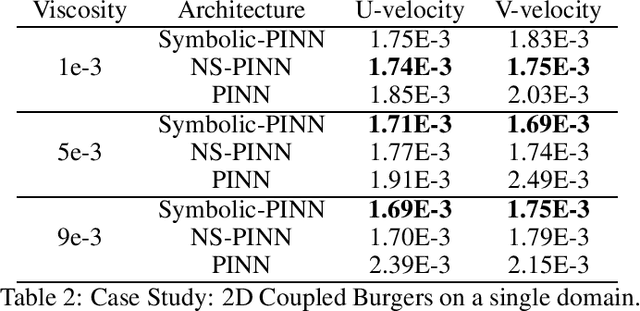
Physics Informed Neural Networks (PINNs) have gained immense popularity as an alternate method for numerically solving PDEs. Despite their empirical success we are still building an understanding of the convergence properties of training on such constraints with gradient descent. It is known that, in the absence of an explicit inductive bias, Neural Networks can struggle to learn or approximate even simple and well known functions in a sample efficient manner. Thus the numerical approximation induced from few collocation points may not generalize over the entire domain. Meanwhile, a symbolic form can exhibit good generalization, with interpretability as a useful byproduct. However, symbolic approximations can struggle to simultaneously be concise and accurate. Therefore in this work we explore a NeuroSymbolic approach to approximate the solution for PDEs. We observe that our approach work for several simple cases. We illustrate the efficacy of our approach on Navier Stokes: Kovasznay flow where there are multiple physical quantities of interest governed with non-linear coupled PDE system. Domain splitting is now becoming a popular trick to help PINNs approximate complex functions. We observe that a NeuroSymbolic approach can help such complex functions as well. We demonstrate Domain-splitting assisted NeuroSymbolic approach on a temporally varying two-dimensional Burger's equation. Finally we consider the scenario where PINNs have to be solved for parameterized PDEs, for changing Initial-Boundary Conditions and changes in the coefficient of the PDEs. Hypernetworks have shown to hold promise to overcome these challenges. We show that one can design Hyper-NeuroSymbolic Networks which can combine the benefits of speed and increased accuracy. We observe that that the NeuroSymbolic approximations are consistently 1-2 order of magnitude better than just the neural or symbolic approximations.