On NeuroSymbolic Solutions for PDEs

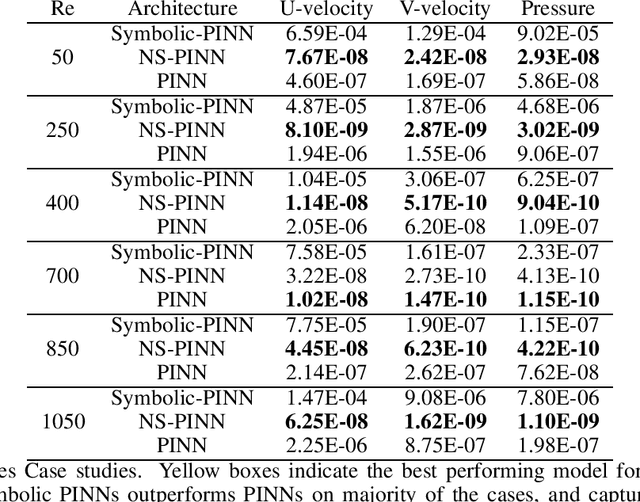
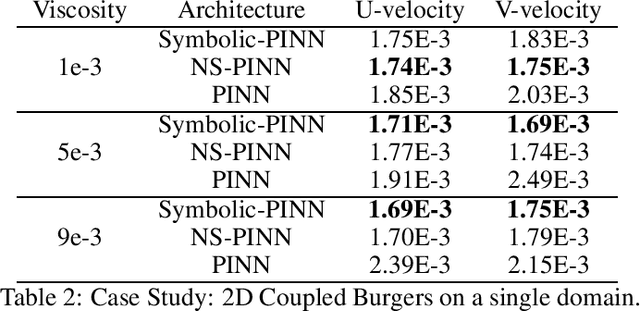
Physics Informed Neural Networks (PINNs) have gained immense popularity as an alternate method for numerically solving PDEs. Despite their empirical success we are still building an understanding of the convergence properties of training on such constraints with gradient descent. It is known that, in the absence of an explicit inductive bias, Neural Networks can struggle to learn or approximate even simple and well known functions in a sample efficient manner. Thus the numerical approximation induced from few collocation points may not generalize over the entire domain. Meanwhile, a symbolic form can exhibit good generalization, with interpretability as a useful byproduct. However, symbolic approximations can struggle to simultaneously be concise and accurate. Therefore in this work we explore a NeuroSymbolic approach to approximate the solution for PDEs. We observe that our approach work for several simple cases. We illustrate the efficacy of our approach on Navier Stokes: Kovasznay flow where there are multiple physical quantities of interest governed with non-linear coupled PDE system. Domain splitting is now becoming a popular trick to help PINNs approximate complex functions. We observe that a NeuroSymbolic approach can help such complex functions as well. We demonstrate Domain-splitting assisted NeuroSymbolic approach on a temporally varying two-dimensional Burger's equation. Finally we consider the scenario where PINNs have to be solved for parameterized PDEs, for changing Initial-Boundary Conditions and changes in the coefficient of the PDEs. Hypernetworks have shown to hold promise to overcome these challenges. We show that one can design Hyper-NeuroSymbolic Networks which can combine the benefits of speed and increased accuracy. We observe that that the NeuroSymbolic approximations are consistently 1-2 order of magnitude better than just the neural or symbolic approximations.