Fairness of Exposure in Online Restless Multi-armed Bandits

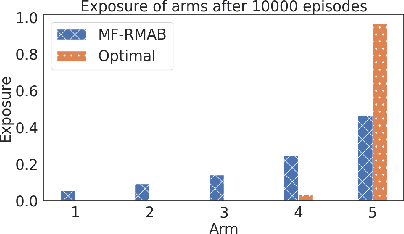
Restless multi-armed bandits (RMABs) generalize the multi-armed bandits where each arm exhibits Markovian behavior and transitions according to their transition dynamics. Solutions to RMAB exist for both offline and online cases. However, they do not consider the distribution of pulls among the arms. Studies have shown that optimal policies lead to unfairness, where some arms are not exposed enough. Existing works in fairness in RMABs focus heavily on the offline case, which diminishes their application in real-world scenarios where the environment is largely unknown. In the online scenario, we propose the first fair RMAB framework, where each arm receives pulls in proportion to its merit. We define the merit of an arm as a function of its stationary reward distribution. We prove that our algorithm achieves sublinear fairness regret in the single pull case $O(\sqrt{T\ln T})$, with $T$ being the total number of episodes. Empirically, we show that our algorithm performs well in the multi-pull scenario as well.

Simultaneously Achieving Group Exposure Fairness and Within-Group Meritocracy in Stochastic Bandits

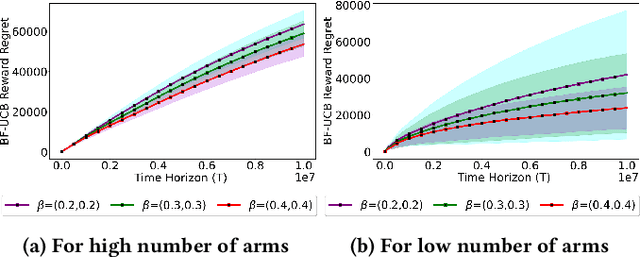
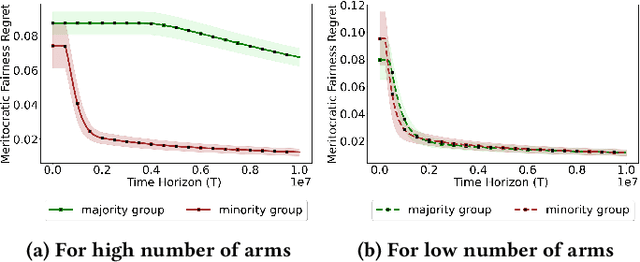
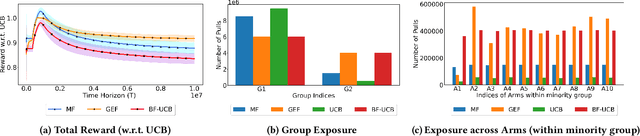
Existing approaches to fairness in stochastic multi-armed bandits (MAB) primarily focus on exposure guarantee to individual arms. When arms are naturally grouped by certain attribute(s), we propose Bi-Level Fairness, which considers two levels of fairness. At the first level, Bi-Level Fairness guarantees a certain minimum exposure to each group. To address the unbalanced allocation of pulls to individual arms within a group, we consider meritocratic fairness at the second level, which ensures that each arm is pulled according to its merit within the group. Our work shows that we can adapt a UCB-based algorithm to achieve a Bi-Level Fairness by providing (i) anytime Group Exposure Fairness guarantees and (ii) ensuring individual-level Meritocratic Fairness within each group. We first show that one can decompose regret bounds into two components: (a) regret due to anytime group exposure fairness and (b) regret due to meritocratic fairness within each group. Our proposed algorithm BF-UCB balances these two regrets optimally to achieve the upper bound of $O(\sqrt{T})$ on regret; $T$ being the stopping time. With the help of simulated experiments, we further show that BF-UCB achieves sub-linear regret; provides better group and individual exposure guarantees compared to existing algorithms; and does not result in a significant drop in reward with respect to UCB algorithm, which does not impose any fairness constraint.

Fairness and Privacy Guarantees in Federated Contextual Bandits

This paper considers the contextual multi-armed bandit (CMAB) problem with fairness and privacy guarantees in a federated environment. We consider merit-based exposure as the desired fair outcome, which provides exposure to each action in proportion to the reward associated. We model the algorithm's effectiveness using fairness regret, which captures the difference between fair optimal policy and the policy output by the algorithm. Applying fair CMAB algorithm to each agent individually leads to fairness regret linear in the number of agents. We propose that collaborative -- federated learning can be more effective and provide the algorithm Fed-FairX-LinUCB that also ensures differential privacy. The primary challenge in extending the existing privacy framework is designing the communication protocol for communicating required information across agents. A naive protocol can either lead to weaker privacy guarantees or higher regret. We design a novel communication protocol that allows for (i) Sub-linear theoretical bounds on fairness regret for Fed-FairX-LinUCB and comparable bounds for the private counterpart, Priv-FairX-LinUCB (relative to single-agent learning), (ii) Effective use of privacy budget in Priv-FairX-LinUCB. We demonstrate the efficacy of our proposed algorithm with extensive simulations-based experiments. We show that both Fed-FairX-LinUCB and Priv-FairX-LinUCB achieve near-optimal fairness regret.

Designing Redistribution Mechanisms for Reducing Transaction Fees in Blockchains

Blockchains deploy Transaction Fee Mechanisms (TFMs) to determine which user transactions to include in blocks and determine their payments (i.e., transaction fees). Increasing demand and scarce block resources have led to high user transaction fees. As these blockchains are a public resource, it may be preferable to reduce these transaction fees. To this end, we introduce Transaction Fee Redistribution Mechanisms (TFRMs) -- redistributing VCG payments collected from such TFM as rebates to minimize transaction fees. Classic redistribution mechanisms (RMs) achieve this while ensuring Allocative Efficiency (AE) and User Incentive Compatibility (UIC). Our first result shows the non-triviality of applying RM in TFMs. More concretely, we prove that it is impossible to reduce transaction fees when (i) transactions that are not confirmed do not receive rebates and (ii) the miner can strategically manipulate the mechanism. Driven by this, we propose \emph{Robust} TFRM (\textsf{R-TFRM}): a mechanism that compromises on an honest miner's individual rationality to guarantee strictly positive rebates to the users. We then introduce \emph{robust} and \emph{rational} TFRM (\textsf{R}$^2$\textsf{-TFRM}) that uses trusted on-chain randomness that additionally guarantees miner's individual rationality (in expectation) and strictly positive rebates. Our results show that TFRMs provide a promising new direction for reducing transaction fees in public blockchains.

A Novel Demand Response Model and Method for Peak Reduction in Smart Grids -- PowerTAC

One of the widely used peak reduction methods in smart grids is demand response, where one analyzes the shift in customers' (agents') usage patterns in response to the signal from the distribution company. Often, these signals are in the form of incentives offered to agents. This work studies the effect of incentives on the probabilities of accepting such offers in a real-world smart grid simulator, PowerTAC. We first show that there exists a function that depicts the probability of an agent reducing its load as a function of the discounts offered to them. We call it reduction probability (RP). RP function is further parametrized by the rate of reduction (RR), which can differ for each agent. We provide an optimal algorithm, MJS--ExpResponse, that outputs the discounts to each agent by maximizing the expected reduction under a budget constraint. When RRs are unknown, we propose a Multi-Armed Bandit (MAB) based online algorithm, namely MJSUCB--ExpResponse, to learn RRs. Experimentally we show that it exhibits sublinear regret. Finally, we showcase the efficacy of the proposed algorithm in mitigating demand peaks in a real-world smart grid system using the PowerTAC simulator as a test bed.

Combinatorial Civic Crowdfunding with Budgeted Agents: Welfare Optimality at Equilibrium and Optimal Deviation

Civic Crowdfunding (CC) uses the ``power of the crowd'' to garner contributions towards public projects. As these projects are non-excludable, agents may prefer to ``free-ride,'' resulting in the project not being funded. For single project CC, researchers propose to provide refunds to incentivize agents to contribute, thereby guaranteeing the project's funding. These funding guarantees are applicable only when agents have an unlimited budget. This work focuses on a combinatorial setting, where multiple projects are available for CC and agents have a limited budget. We study certain specific conditions where funding can be guaranteed. Further, funding the optimal social welfare subset of projects is desirable when every available project cannot be funded due to budget restrictions. We prove the impossibility of achieving optimal welfare at equilibrium for any monotone refund scheme. We then study different heuristics that the agents can use to contribute to the projects in practice. Through simulations, we demonstrate the heuristics' performance as the average-case trade-off between welfare obtained and agent utility.

Differentially Private Federated Combinatorial Bandits with Constraints

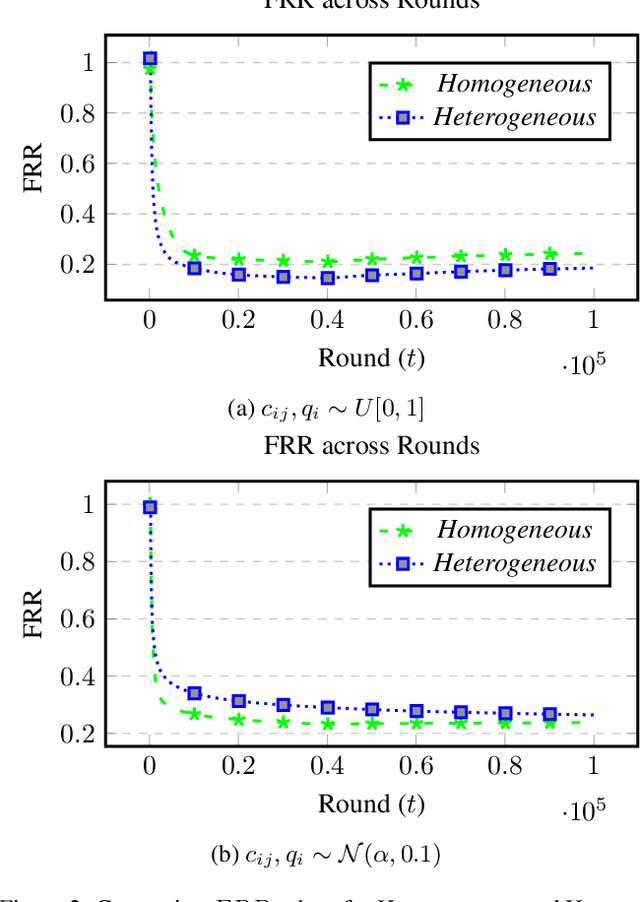
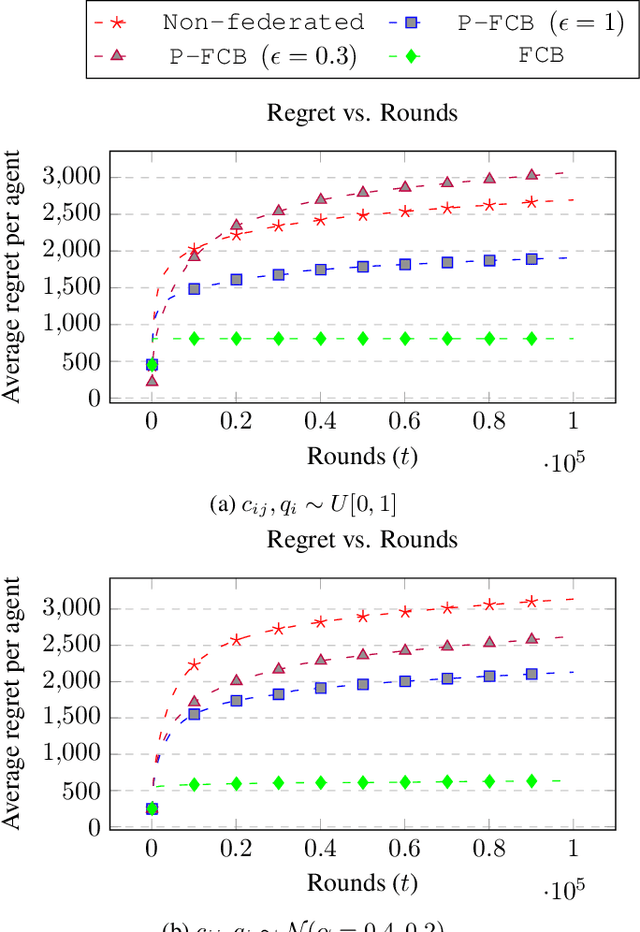
There is a rapid increase in the cooperative learning paradigm in online learning settings, i.e., federated learning (FL). Unlike most FL settings, there are many situations where the agents are competitive. Each agent would like to learn from others, but the part of the information it shares for others to learn from could be sensitive; thus, it desires its privacy. This work investigates a group of agents working concurrently to solve similar combinatorial bandit problems while maintaining quality constraints. Can these agents collectively learn while keeping their sensitive information confidential by employing differential privacy? We observe that communicating can reduce the regret. However, differential privacy techniques for protecting sensitive information makes the data noisy and may deteriorate than help to improve regret. Hence, we note that it is essential to decide when to communicate and what shared data to learn to strike a functional balance between regret and privacy. For such a federated combinatorial MAB setting, we propose a Privacy-preserving Federated Combinatorial Bandit algorithm, P-FCB. We illustrate the efficacy of P-FCB through simulations. We further show that our algorithm provides an improvement in terms of regret while upholding quality threshold and meaningful privacy guarantees.

Budgeted Combinatorial Multi-Armed Bandits

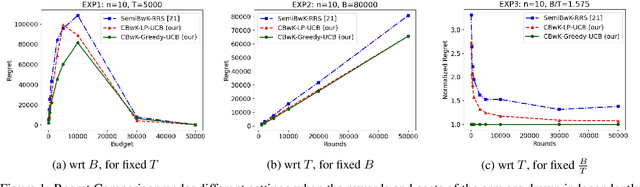
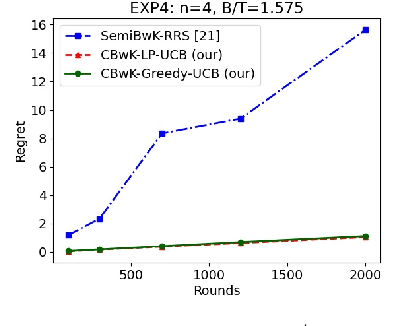
We consider a budgeted combinatorial multi-armed bandit setting where, in every round, the algorithm selects a super-arm consisting of one or more arms. The goal is to minimize the total expected regret after all rounds within a limited budget. Existing techniques in this literature either fix the budget per round or fix the number of arms pulled in each round. Our setting is more general where based on the remaining budget and remaining number of rounds, the algorithm can decide how many arms to be pulled in each round. First, we propose CBwK-Greedy-UCB algorithm, which uses a greedy technique, CBwK-Greedy, to allocate the arms to the rounds. Next, we propose a reduction of this problem to Bandits with Knapsacks (BwK) with a single pull. With this reduction, we propose CBwK-LPUCB that uses PrimalDualBwK ingeniously. We rigorously prove regret bounds for CBwK-LP-UCB. We experimentally compare the two algorithms and observe that CBwK-Greedy-UCB performs incrementally better than CBwK-LP-UCB. We also show that for very high budgets, the regret goes to zero.

Fair Federated Learning for Heterogeneous Face Data

We consider the problem of achieving fair classification in Federated Learning (FL) under data heterogeneity. Most of the approaches proposed for fair classification require diverse data that represent the different demographic groups involved. In contrast, it is common for each client to own data that represents only a single demographic group. Hence the existing approaches cannot be adopted for fair classification models at the client level. To resolve this challenge, we propose several aggregation techniques. We empirically validate these techniques by comparing the resulting fairness metrics and accuracy on CelebA, UTK, and FairFace datasets.

Federated Learning Meets Fairness and Differential Privacy

Deep learning's unprecedented success raises several ethical concerns ranging from biased predictions to data privacy. Researchers tackle these issues by introducing fairness metrics, or federated learning, or differential privacy. A first, this work presents an ethical federated learning model, incorporating all three measures simultaneously. Experiments on the Adult, Bank and Dutch datasets highlight the resulting ``empirical interplay" between accuracy, fairness, and privacy.