FROC: Building Fair ROC from a Trained Classifier

This paper considers the problem of fair probabilistic binary classification with binary protected groups. The classifier assigns scores, and a practitioner predicts labels using a certain cut-off threshold based on the desired trade-off between false positives vs. false negatives. It derives these thresholds from the ROC of the classifier. The resultant classifier may be unfair to one of the two protected groups in the dataset. It is desirable that no matter what threshold the practitioner uses, the classifier should be fair to both the protected groups; that is, the $\mathcal{L}_p$ norm between FPRs and TPRs of both the protected groups should be at most $\varepsilon$. We call such fairness on ROCs of both the protected attributes $\varepsilon_p$-Equalized ROC. Given a classifier not satisfying $\varepsilon_1$-Equalized ROC, we aim to design a post-processing method to transform the given (potentially unfair) classifier's output (score) to a suitable randomized yet fair classifier. That is, the resultant classifier must satisfy $\varepsilon_1$-Equalized ROC. First, we introduce a threshold query model on the ROC curves for each protected group. The resulting classifier is bound to face a reduction in AUC. With the proposed query model, we provide a rigorous theoretical analysis of the minimal AUC loss to achieve $\varepsilon_1$-Equalized ROC. To achieve this, we design a linear time algorithm, namely \texttt{FROC}, to transform a given classifier's output to a probabilistic classifier that satisfies $\varepsilon_1$-Equalized ROC. We prove that under certain theoretical conditions, \texttt{FROC}\ achieves the theoretical optimal guarantees. We also study the performance of our \texttt{FROC}\ on multiple real-world datasets with many trained classifiers.

Oblivious Permutations on the Plane

We consider a distributed system of n identical mobile robots operating in the two dimensional Euclidian plane. As in the previous studies, we consider the robots to be anonymous, oblivious, dis-oriented, and without any communication capabilities, operating based on the Look-Compute-Move model where the next location of a robot depends only on its view of the current configuration. Even in this seemingly weak model, most formation problems which require constructing specific configurations, can be solved quite easily when the robots are fully synchronized with each other. In this paper we introduce and study a new class of problems which, unlike the formation problems so far, cannot always be solved even in the fully synchronous model with atomic and rigid moves. This class of problems requires the robots to permute their locations in the plane. In particular, we are interested in implementing two special types of permutations -- permutations without any fixed points and permutations of order $n$. The former (called MOVE-ALL) requires each robot to visit at least two of the initial locations, while the latter (called VISIT-ALL) requires every robot to visit each of the initial locations in a periodic manner. We provide a characterization of the solvability of these problems, showing the main challenges in solving this class of problems for mobile robots. We also provide algorithms for the feasible cases, in particular distinguishing between one-step algorithms (where each configuration must be a permutation of the original configuration) and multi-step algorithms (which allow intermediate configurations). These results open a new research direction in mobile distributed robotics which has not been investigated before.

Multi-objective Active Control Policy Design for Commensurate and Incommensurate Fractional Order Chaotic Financial Systems

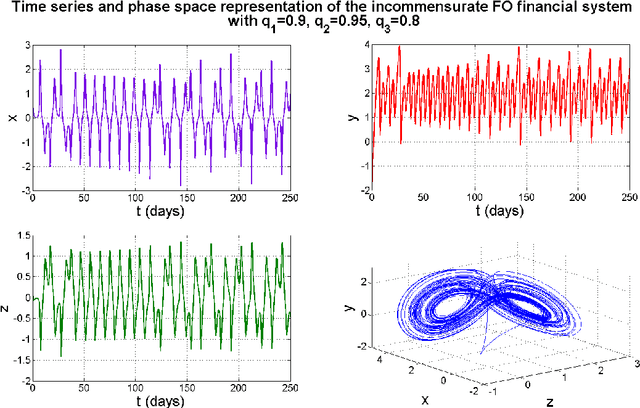
In this paper, an active control policy design for a fractional order (FO) financial system is attempted, considering multiple conflicting objectives. An active control template as a nonlinear state feedback mechanism is developed and the controller gains are chosen within a multi-objective optimization (MOO) framework to satisfy the conditions of asymptotic stability, derived analytically. The MOO gives a set of solutions on the Pareto optimal front for the multiple conflicting objectives that are considered. It is shown that there is a trade-off between the multiple design objectives and a better performance in one objective can only be obtained at the cost of performance deterioration in the other objectives. The multi-objective controller design has been compared using three different MOO techniques viz. Non Dominated Sorting Genetic Algorithm-II (NSGA-II), epsilon variable Multi-Objective Genetic Algorithm (ev-MOGA), and Multi Objective Evolutionary Algorithm with Decomposition (MOEA/D). The robustness of the same control policy designed with the nominal system settings have been investigated also for gradual decrease in the commensurate and incommensurate fractional orders of the financial system.

Artificial Neural Network Based Prediction of Optimal Pseudo-Damping and Meta-Damping in Oscillatory Fractional Order Dynamical Systems

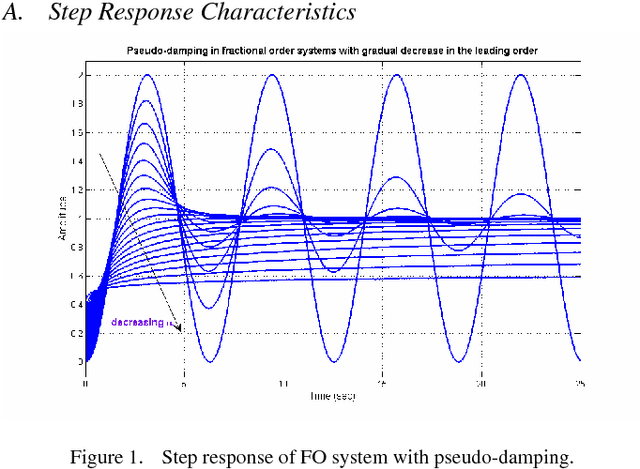
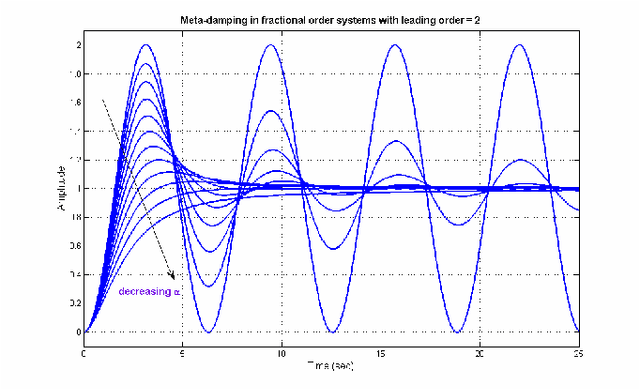
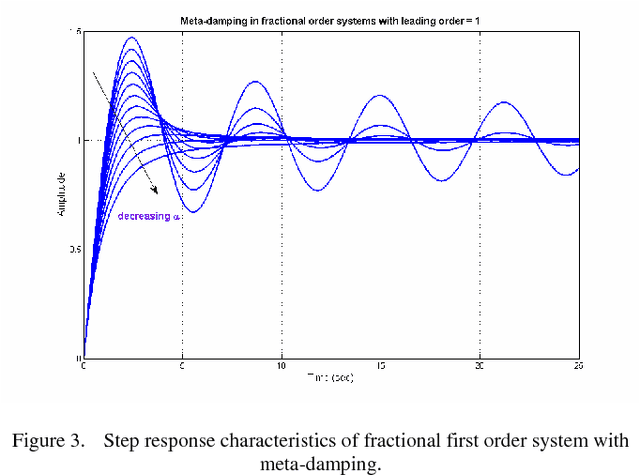
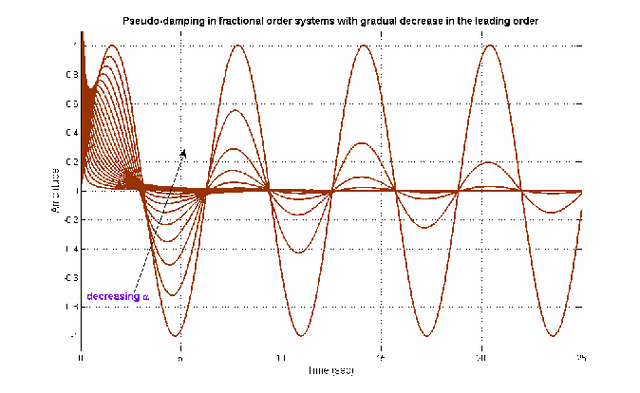
This paper investigates typical behaviors like damped oscillations in fractional order (FO) dynamical systems. Such response occurs due to the presence of, what is conceived as, pseudo-damping and meta-damping in some special class of FO systems. Here, approximation of such damped oscillation in FO systems with the conventional notion of integer order damping and time constant has been carried out using Genetic Algorithm (GA). Next, a multilayer feed-forward Artificial Neural Network (ANN) has been trained using the GA based results to predict the optimal pseudo and meta-damping from knowledge of the maximum order or number of terms in the FO dynamical system.

Wait-Free Gathering of Mobile Robots

The problem of gathering multiple mobile robots to a single location, is one of the fundamental problems in distributed coordination between autonomous robots. The problem has been studied and solved even for robots that are anonymous, disoriented, memoryless and operate in the semi-synchronous (ATOM) model. However all known solutions require the robots to be faulty-free except for the results of [Agmon and Peleg 2006] who solve the gathering problem in presence of one crash fault. This leaves open the question of whether gathering of correct robots can be achieved in the presence of multiple crash failures. We resolve the question in this paper and show how to solve gathering, when any number of robots may crash at any time during the algorithm, assuming strong multiplicity detection and chirality. In contrast it is known that for the more stronger byzantine faults, it is impossible to gather even in a 3-robot system if one robot is faulty. Our algorithm solves the gathering of correct robots in the semi-synchronous model where an adversary may stop any robot before reaching its desired destination. Further the algorithm is self-stabilizing as it achieves gathering starting from any configuration (except the bivalent configuration where deterministic gathering is impossible).

Improved Model Reduction and Tuning of Fractional Order PIλDμ Controllers for Analytical Rule Extraction with Genetic Programming

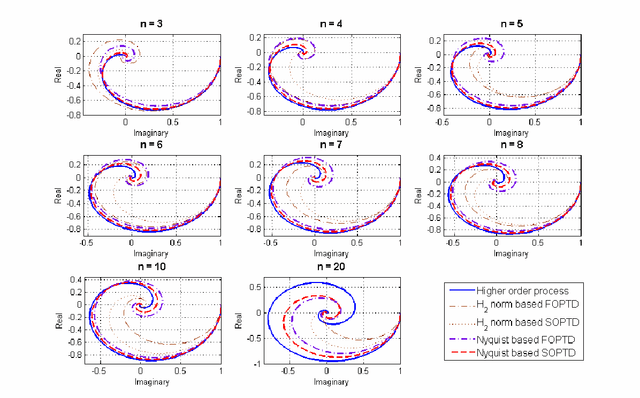
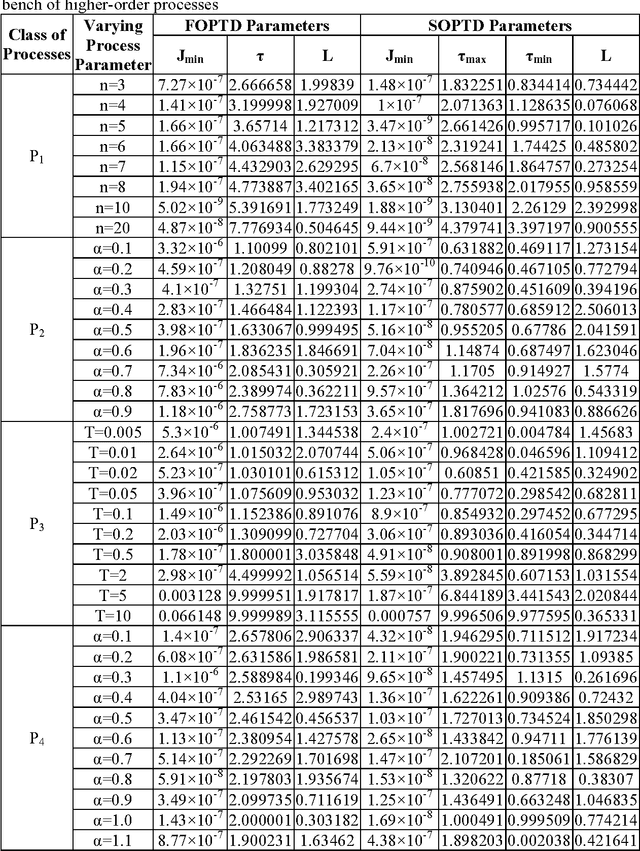
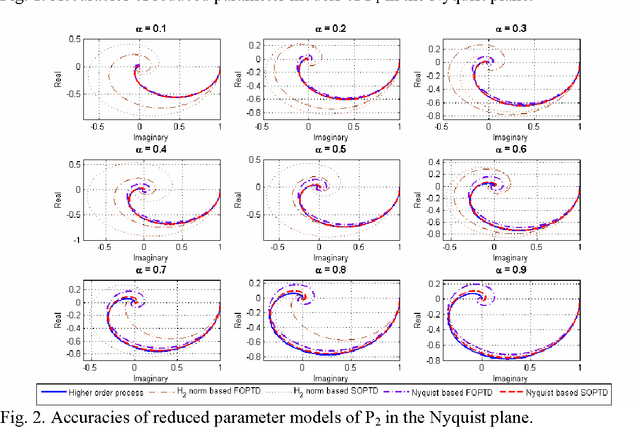
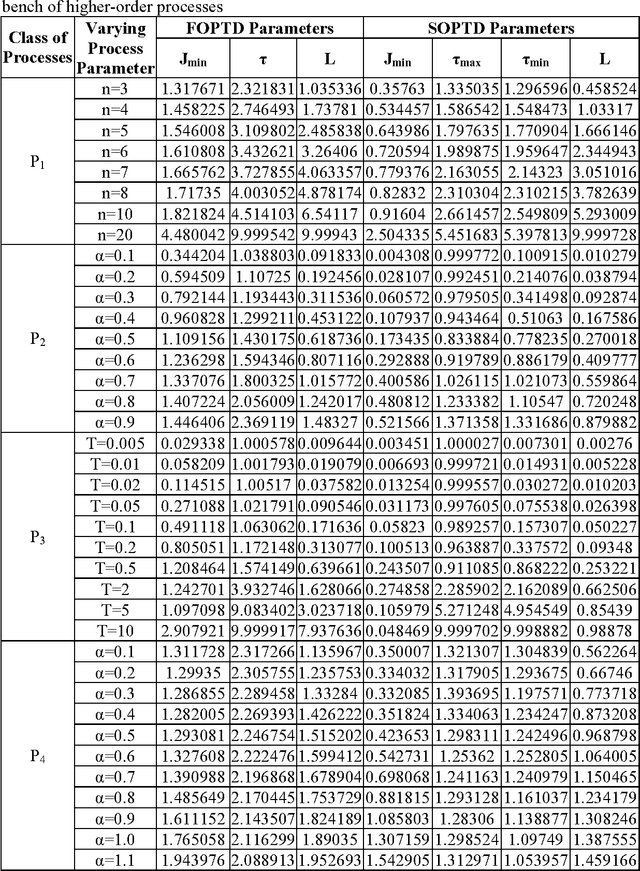
Genetic Algorithm (GA) has been used in this paper for a new approach of sub-optimal model reduction in the Nyquist plane and optimal time domain tuning of PID and fractional order (FO) PI{\lambda}D{\mu} controllers. Simulation studies show that the Nyquist based new model reduction technique outperforms the conventional H2 norm based reduced parameter modeling technique. With the tuned controller parameters and reduced order model parameter data-set, optimum tuning rules have been developed with a test-bench of higher order processes via Genetic Programming (GP). The GP performs a symbolic regression on the reduced process parameters to evolve a tuning rule which provides the best analytical expression to map the data. The tuning rules are developed for a minimum time domain integral performance index described by weighted sum of error index and controller effort. From the reported Pareto optimal front of GP based optimal rule extraction technique a trade-off can be made between the complexity of the tuning formulae and the control performance. The efficacy of the single-gene and multi-gene GP based tuning rules has been compared with original GA based control performance for the PID and PI{\lambda}D{\mu} controllers, handling four different class of representative higher order processes. These rules are very useful for process control engineers as they inherit the power of the GA based tuning methodology, but can be easily calculated without the requirement for running the computationally intensive GA every time. Three dimensional plots of the required variation in PID/FOPID controller parameters with reduced process parameters have been shown as a guideline for the operator. Parametric robustness of the reported GP based tuning rules has also been shown with credible simulation examples.