Synchronization by Asynchronous Mobile Robots with Limited Visibility

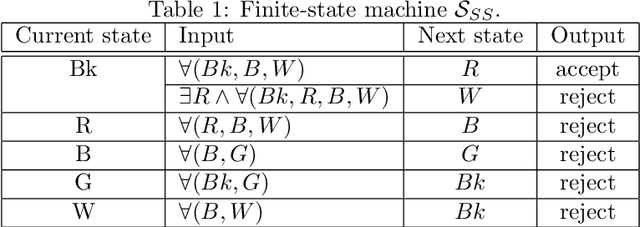
A mobile robot system consists of anonymous mobile robots, each of which autonomously performs sensing, computation, and movement according to a common algorithm, so that the robots collectively achieve a given task. There are two main models of time and activation of the robots. In the semi-synchronous model (SSYNC), the robots share a common notion of time; at each time unit, a subset of the robots is activated, and each performs all three actions (sensing, computation, and movement) in that time unit. In the asynchronous model (ASYNC), there is no common notion of time, the robots are activated at arbitrary times, and the duration of each action is arbitrary but finite. In this paper, we investigate the problem of synchronizing ASNYC robots with limited sensing range, i.e., limited visibility. We first present a sufficient condition for an ASYNC execution of a common algorithm ${\cal A}$ to have a corresponding SSYNC execution of ${\cal A}$; our condition imposes timing constraints on the activation schedule of the robots and visibility constraints during movement. Then, we prove that this condition is necessary (with probability $1$) under a randomized ASYNC adversary. Finally, we present a synchronization algorithm for luminous ASYNC robots with limited visibility, each equipped with a light that can take a constant number of colors. Our algorithm enables luminous ASYNC robots to simulate any algorithm ${\cal A}$, designed for the (non-luminous) SSYNC robots and satisfying visibility constraints.

Oblivious Permutations on the Plane

We consider a distributed system of n identical mobile robots operating in the two dimensional Euclidian plane. As in the previous studies, we consider the robots to be anonymous, oblivious, dis-oriented, and without any communication capabilities, operating based on the Look-Compute-Move model where the next location of a robot depends only on its view of the current configuration. Even in this seemingly weak model, most formation problems which require constructing specific configurations, can be solved quite easily when the robots are fully synchronized with each other. In this paper we introduce and study a new class of problems which, unlike the formation problems so far, cannot always be solved even in the fully synchronous model with atomic and rigid moves. This class of problems requires the robots to permute their locations in the plane. In particular, we are interested in implementing two special types of permutations -- permutations without any fixed points and permutations of order $n$. The former (called MOVE-ALL) requires each robot to visit at least two of the initial locations, while the latter (called VISIT-ALL) requires every robot to visit each of the initial locations in a periodic manner. We provide a characterization of the solvability of these problems, showing the main challenges in solving this class of problems for mobile robots. We also provide algorithms for the feasible cases, in particular distinguishing between one-step algorithms (where each configuration must be a permutation of the original configuration) and multi-step algorithms (which allow intermediate configurations). These results open a new research direction in mobile distributed robotics which has not been investigated before.

Exploration of Finite 2D Square Grid by a Metamorphic Robotic System

We consider exploration of finite 2D square grid by a metamorphic robotic system consisting of anonymous oblivious modules. The number of possible shapes of a metamorphic robotic system grows as the number of modules increases. The shape of the system serves as its memory and shows its functionality. We consider the effect of global compass on the minimum number of modules necessary to explore a finite 2D square grid. We show that if the modules agree on the directions (north, south, east, and west), three modules are necessary and sufficient for exploration from an arbitrary initial configuration, otherwise five modules are necessary and sufficient for restricted initial configurations.

Meeting in a Polygon by Anonymous Oblivious Robots

The Meeting problem for $k\geq 2$ searchers in a polygon $P$ (possibly with holes) consists in making the searchers move within $P$, according to a distributed algorithm, in such a way that at least two of them eventually come to see each other, regardless of their initial positions. The polygon is initially unknown to the searchers, and its edges obstruct both movement and vision. Depending on the shape of $P$, we minimize the number of searchers $k$ for which the Meeting problem is solvable. Specifically, if $P$ has a rotational symmetry of order $\sigma$ (where $\sigma=1$ corresponds to no rotational symmetry), we prove that $k=\sigma+1$ searchers are sufficient, and the bound is tight. Furthermore, we give an improved algorithm that optimally solves the Meeting problem with $k=2$ searchers in all polygons whose barycenter is not in a hole (which includes the polygons with no holes). Our algorithms can be implemented in a variety of standard models of mobile robots operating in Look-Compute-Move cycles. For instance, if the searchers have memory but are anonymous, asynchronous, and have no agreement on a coordinate system or a notion of clockwise direction, then our algorithms work even if the initial memory contents of the searchers are arbitrary and possibly misleading. Moreover, oblivious searchers can execute our algorithms as well, encoding information by carefully positioning themselves within the polygon. This code is computable with basic arithmetic operations, and each searcher can geometrically construct its own destination point at each cycle using only a compass. We stress that such memoryless searchers may be located anywhere in the polygon when the execution begins, and hence the information they initially encode is arbitrary. Our algorithms use a self-stabilizing map construction subroutine which is of independent interest.

Plane Formation by Synchronous Mobile Robots in the Three Dimensional Euclidean Space

Creating a swarm of mobile computing entities frequently called robots, agents or sensor nodes, with self-organization ability is a contemporary challenge in distributed computing. Motivated by this, we investigate the plane formation problem that requires a swarm of robots moving in the three dimensional Euclidean space to land on a common plane. The robots are fully synchronous and endowed with visual perception. But they do not have identifiers, nor access to the global coordinate system, nor any means of explicit communication with each other. Though there are plenty of results on the agreement problem for robots in the two dimensional plane, for example, the point formation problem, the pattern formation problem, and so on, this is the first result for robots in the three dimensional space. This paper presents a necessary and sufficient condition for fully-synchronous robots to solve the plane formation problem that does not depend on obliviousness i.e., the availability of local memory at robots. An implication of the result is somewhat counter-intuitive: The robots cannot form a plane from most of the semi-regular polyhedra, while they can form a plane from every regular polyhedron (except a regular icosahedron), whose symmetry is usually considered to be higher than any semi-regular polyhedrdon.

Rendezvous of Two Robots with Constant Memory

We study the impact that persistent memory has on the classical rendezvous problem of two mobile computational entities, called robots, in the plane. It is well known that, without additional assumptions, rendezvous is impossible if the entities are oblivious (i.e., have no persistent memory) even if the system is semi-synchronous (SSynch). It has been recently shown that rendezvous is possible even if the system is asynchronous (ASynch) if each robot is endowed with O(1) bits of persistent memory, can transmit O(1) bits in each cycle, and can remember (i.e., can persistently store) the last received transmission. This setting is overly powerful. In this paper we weaken that setting in two different ways: (1) by maintaining the O(1) bits of persistent memory but removing the communication capabilities; and (2) by maintaining the O(1) transmission capability and the ability to remember the last received transmission, but removing the ability of an agent to remember its previous activities. We call the former setting finite-state (FState) and the latter finite-communication (FComm). Note that, even though its use is very different, in both settings, the amount of persistent memory of a robot is constant. We investigate the rendezvous problem in these two weaker settings. We model both settings as a system of robots endowed with visible lights: in FState, a robot can only see its own light, while in FComm a robot can only see the other robot's light. We prove, among other things, that finite-state robots can rendezvous in SSynch, and that finite-communication robots are able to rendezvous even in ASynch. All proofs are constructive: in each setting, we present a protocol that allows the two robots to rendezvous in finite time.

Expressivity of Time-Varying Graphs and the Power of Waiting in Dynamic Networks

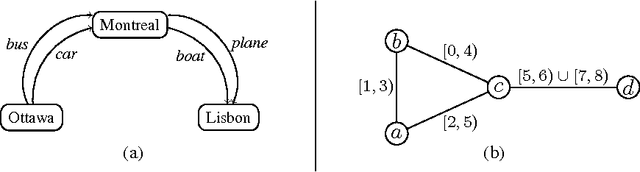
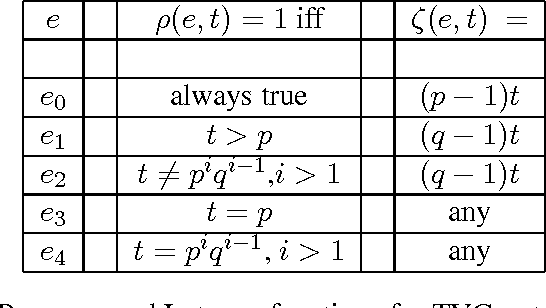
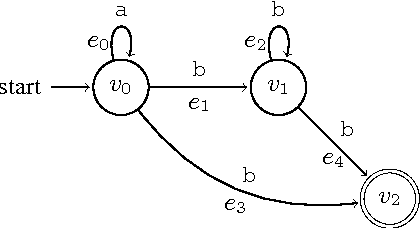
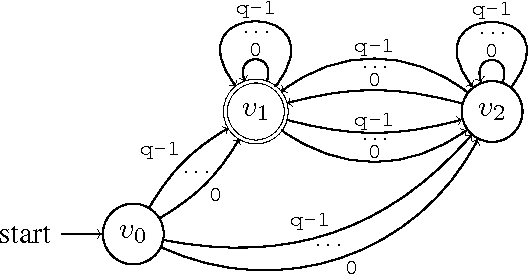
In infrastructure-less highly dynamic networks, computing and performing even basic tasks (such as routing and broadcasting) is a very challenging activity due to the fact that connectivity does not necessarily hold, and the network may actually be disconnected at every time instant. Clearly the task of designing protocols for these networks is less difficult if the environment allows waiting (i.e., it provides the nodes with store-carry-forward-like mechanisms such as local buffering) than if waiting is not feasible. No quantitative corroborations of this fact exist (e.g., no answer to the question: how much easier?). In this paper, we consider these qualitative questions about dynamic networks, modeled as time-varying (or evolving) graphs, where edges exist only at some times. We examine the difficulty of the environment in terms of the expressivity of the corresponding time-varying graph; that is in terms of the language generated by the feasible journeys in the graph. We prove that the set of languages $L_{nowait}$ when no waiting is allowed contains all computable languages. On the other end, using algebraic properties of quasi-orders, we prove that $L_{wait}$ is just the family of regular languages. In other words, we prove that, when waiting is no longer forbidden, the power of the accepting automaton (difficulty of the environment) drops drastically from being as powerful as a Turing machine, to becoming that of a Finite-State machine. This (perhaps surprisingly large) gap is a measure of the computational power of waiting. We also study bounded waiting; that is when waiting is allowed at a node only for at most $d$ time units. We prove the negative result that $L_{wait[d]} = L_{nowait}$; that is, the expressivity decreases only if the waiting is finite but unpredictable (i.e., under the control of the protocol designer and not of the environment).

The Gathering Problem for Two Oblivious Robots with Unreliable Compasses

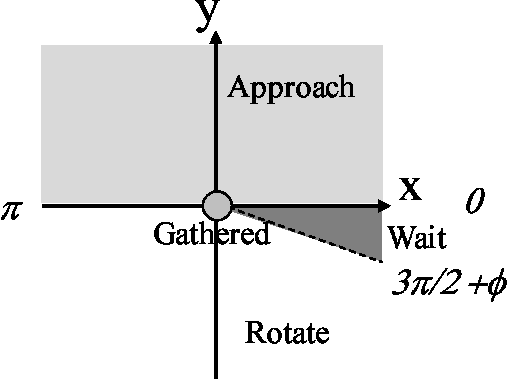
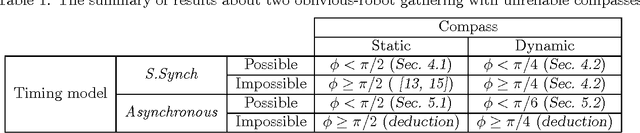
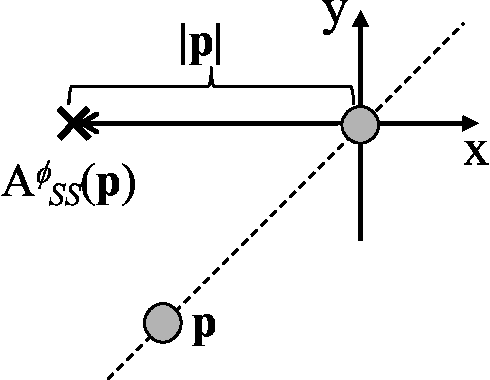
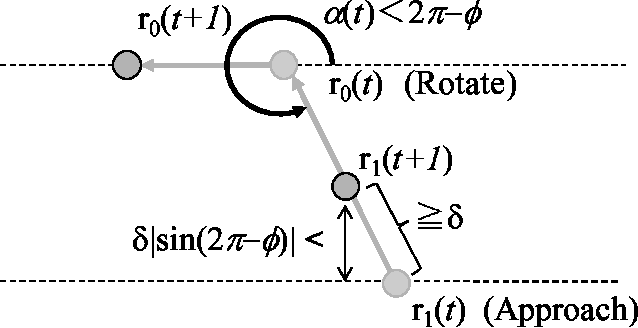
Anonymous mobile robots are often classified into synchronous, semi-synchronous and asynchronous robots when discussing the pattern formation problem. For semi-synchronous robots, all patterns formable with memory are also formable without memory, with the single exception of forming a point (i.e., the gathering) by two robots. However, the gathering problem for two semi-synchronous robots without memory is trivially solvable when their local coordinate systems are consistent, and the impossibility proof essentially uses the inconsistencies in their coordinate systems. Motivated by this, this paper investigates the magnitude of consistency between the local coordinate systems necessary and sufficient to solve the gathering problem for two oblivious robots under semi-synchronous and asynchronous models. To discuss the magnitude of consistency, we assume that each robot is equipped with an unreliable compass, the bearings of which may deviate from an absolute reference direction, and that the local coordinate system of each robot is determined by its compass. We consider two families of unreliable compasses, namely,static compasses with constant bearings, and dynamic compasses the bearings of which can change arbitrarily. For each of the combinations of robot and compass models, we establish the condition on deviation \phi that allows an algorithm to solve the gathering problem, where the deviation is measured by the largest angle formed between the x-axis of a compass and the reference direction of the global coordinate system: \phi < \pi/2 for semi-synchronous and asynchronous robots with static compasses, \phi < \pi/4 for semi-synchronous robots with dynamic compasses, and \phi < \pi/6 for asynchronous robots with dynamic compasses. Except for asynchronous robots with dynamic compasses, these sufficient conditions are also necessary.