Gathering on a Circle with Limited Visibility by Anonymous Oblivious Robots

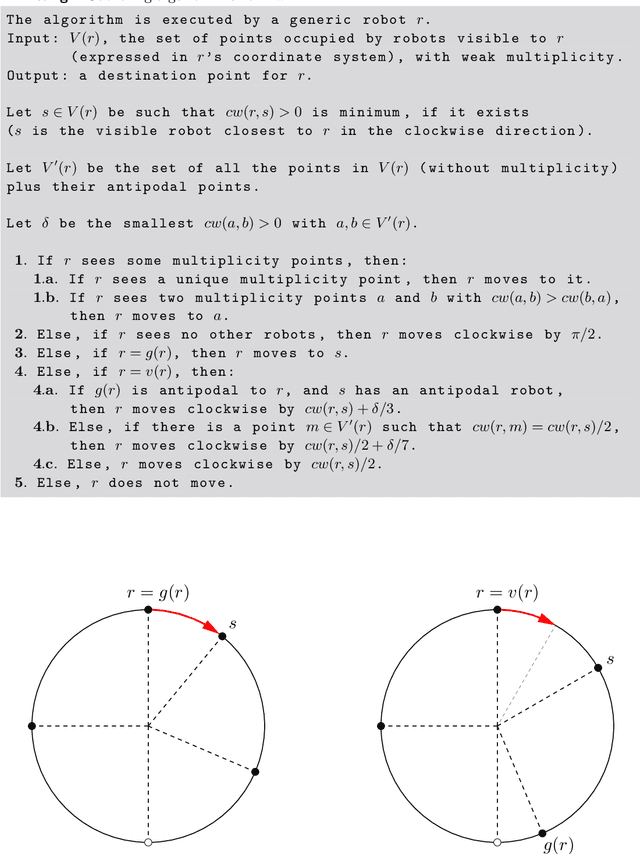
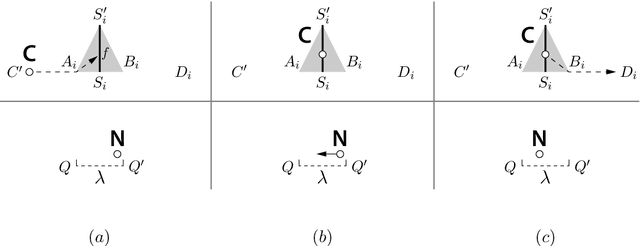
A swarm of anonymous oblivious mobile robots, operating in deterministic Look-Compute-Move cycles, is confined within a circular track. All robots agree on the clockwise direction (chirality), they are activated by an adversarial semi-synchronous scheduler (SSYNCH), and an active robot always reaches the destination point it computes (rigidity). Robots have limited visibility: each robot can see only the points on the circle that have an angular distance strictly smaller than a constant $\vartheta$ from the robot's current location, where $0<\vartheta\leq\pi$ (angles are expressed in radians). We study the Gathering problem for such a swarm of robots: that is, all robots are initially in distinct locations on the circle, and their task is to reach the same point on the circle in a finite number of turns, regardless of the way they are activated by the scheduler. Note that, due to the anonymity of the robots, this task is impossible if the initial configuration is rotationally symmetric; hence, we have to make the assumption that the initial configuration be rotationally asymmetric. We prove that, if $\vartheta=\pi$ (i.e., each robot can see the entire circle except its antipodal point), there is a distributed algorithm that solves the Gathering problem for swarms of any size. By contrast, we also prove that, if $\vartheta\leq \pi/2$, no distributed algorithm solves the Gathering problem, regardless of the size of the swarm, even under the assumption that the initial configuration is rotationally asymmetric and the visibility graph of the robots is connected. The latter impossibility result relies on a probabilistic technique based on random perturbations, which is novel in the context of anonymous mobile robots. Such a technique is of independent interest, and immediately applies to other Pattern-Formation problems.

Oblivious Permutations on the Plane

We consider a distributed system of n identical mobile robots operating in the two dimensional Euclidian plane. As in the previous studies, we consider the robots to be anonymous, oblivious, dis-oriented, and without any communication capabilities, operating based on the Look-Compute-Move model where the next location of a robot depends only on its view of the current configuration. Even in this seemingly weak model, most formation problems which require constructing specific configurations, can be solved quite easily when the robots are fully synchronized with each other. In this paper we introduce and study a new class of problems which, unlike the formation problems so far, cannot always be solved even in the fully synchronous model with atomic and rigid moves. This class of problems requires the robots to permute their locations in the plane. In particular, we are interested in implementing two special types of permutations -- permutations without any fixed points and permutations of order $n$. The former (called MOVE-ALL) requires each robot to visit at least two of the initial locations, while the latter (called VISIT-ALL) requires every robot to visit each of the initial locations in a periodic manner. We provide a characterization of the solvability of these problems, showing the main challenges in solving this class of problems for mobile robots. We also provide algorithms for the feasible cases, in particular distinguishing between one-step algorithms (where each configuration must be a permutation of the original configuration) and multi-step algorithms (which allow intermediate configurations). These results open a new research direction in mobile distributed robotics which has not been investigated before.

TuringMobile: A Turing Machine of Oblivious Mobile Robots with Limited Visibility and its Applications

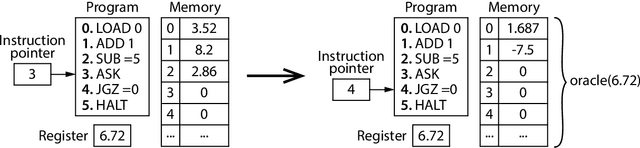
In this paper we investigate the computational power of a set of mobile robots with limited visibility. At each iteration, a robot takes a snapshot of its surroundings, uses the snapshot to compute a destination point, and it moves toward its destination. Each robot is punctiform and memoryless, it operates in $\mathbb{R}^m$, it has a local reference system independent of the other robots' ones, and is activated asynchronously by an adversarial scheduler. Moreover, robots are non-rigid, in that they may be stopped by the scheduler at each move before reaching their destination (but are guaranteed to travel at least a fixed unknown distance before being stopped). We show that despite these strong limitations, it is possible to arrange $3m+3k$ of these weak entities in $\mathbb{R}^m$ to simulate the behavior of a stronger robot that is rigid (i.e., it always reaches its destination) and is endowed with $k$ registers of persistent memory, each of which can store a real number. We call this arrangement a TuringMobile. In its simplest form, a TuringMobile consisting of only three robots can travel in the plane and store and update a single real number. We also prove that this task is impossible with fewer than three robots. Among the applications of the TuringMobile, we focused on Near-Gathering (all robots have to gather in a small-enough disk) and Pattern Formation (of which Gathering is a special case) with limited visibility. Interestingly, our investigation implies that both problems are solvable in Euclidean spaces of any dimension, even if the visibility graph of the robots is initially disconnected, provided that a small amount of these robots are arranged to form a TuringMobile. In the special case of the plane, a basic TuringMobile of only three robots is sufficient.

Meeting in a Polygon by Anonymous Oblivious Robots

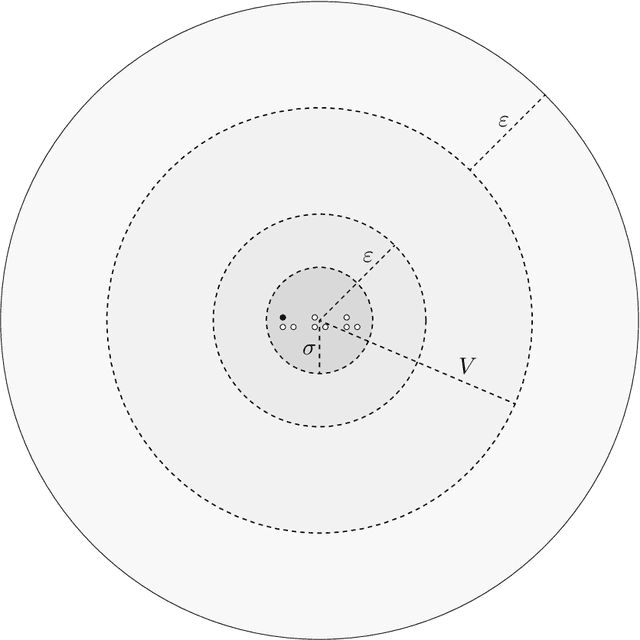
The Meeting problem for $k\geq 2$ searchers in a polygon $P$ (possibly with holes) consists in making the searchers move within $P$, according to a distributed algorithm, in such a way that at least two of them eventually come to see each other, regardless of their initial positions. The polygon is initially unknown to the searchers, and its edges obstruct both movement and vision. Depending on the shape of $P$, we minimize the number of searchers $k$ for which the Meeting problem is solvable. Specifically, if $P$ has a rotational symmetry of order $\sigma$ (where $\sigma=1$ corresponds to no rotational symmetry), we prove that $k=\sigma+1$ searchers are sufficient, and the bound is tight. Furthermore, we give an improved algorithm that optimally solves the Meeting problem with $k=2$ searchers in all polygons whose barycenter is not in a hole (which includes the polygons with no holes). Our algorithms can be implemented in a variety of standard models of mobile robots operating in Look-Compute-Move cycles. For instance, if the searchers have memory but are anonymous, asynchronous, and have no agreement on a coordinate system or a notion of clockwise direction, then our algorithms work even if the initial memory contents of the searchers are arbitrary and possibly misleading. Moreover, oblivious searchers can execute our algorithms as well, encoding information by carefully positioning themselves within the polygon. This code is computable with basic arithmetic operations, and each searcher can geometrically construct its own destination point at each cycle using only a compass. We stress that such memoryless searchers may be located anywhere in the polygon when the execution begins, and hence the information they initially encode is arbitrary. Our algorithms use a self-stabilizing map construction subroutine which is of independent interest.

Shape Formation by Programmable Particles

Shape formation is a basic distributed problem for systems of computational mobile entities. Intensively studied for systems of autonomous mobile robots, it has recently been investigated in the realm of programmable matter. Namely, it has been studied in the geometric Amoebot model, where the anonymous entities, called particles, operate on a hexagonal tessellation of the plane and have limited computational power (they have constant memory), strictly local interaction and communication capabilities (only with particles in neighboring nodes of the grid), and limited motorial capabilities (from a grid node to an empty neighboring node); their activation is controlled by an adversarial scheduler. Recent investigations have shown how, starting from a well-structured configuration in which the particles form a (not necessarily complete) triangle, the particles can form a large class of shapes. This result has been established under several assumptions: agreement on the clockwise direction (i.e., chirality), a sequential activation schedule, and randomization (i.e., particles can flip coins). In this paper we provide a characterization of which shapes can be formed deterministically starting from any simply connected initial configuration of $n$ particles. As a byproduct, if randomization is allowed, then any input shape can be formed from any initial (simply connected) shape by our algorithm, provided that $n$ is large enough. Our algorithm works without chirality, proving that chirality is computationally irrelevant for shape formation. Furthermore, it works under a strong adversarial scheduler, not necessarily sequential. We also consider the complexity of shape formation in terms of both the number of rounds and of moves performed by the particles. We prove that our solution has a complexity of $O(n^2)$ rounds and moves: this number of moves is also asymptotically optimal.

Square Formation by Asynchronous Oblivious Robots

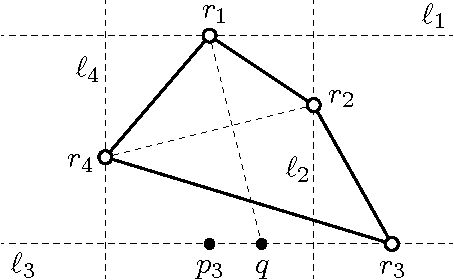
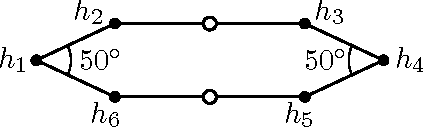
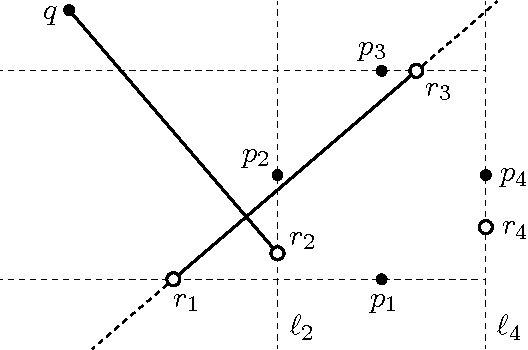
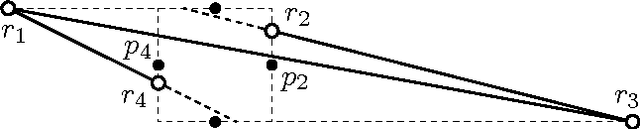
A fundamental problem in Distributed Computing is the Pattern Formation problem, where some independent mobile entities, called robots, have to rearrange themselves in such a way as to form a given figure from every possible (non-degenerate) initial configuration. In the present paper, we consider robots that operate in the Euclidean plane and are dimensionless, anonymous, oblivious, silent, asynchronous, disoriented, non-chiral, and non-rigid. For this very elementary type of robots, the feasibility of the Pattern Formation problem has been settled, either in the positive or in the negative, for every possible pattern, except for one case: the Square Formation problem by a team of four robots. Here we solve this last case by giving a Square Formation algorithm and proving its correctness. Our contribution represents the concluding chapter in a long thread of research. Our results imply that in the context of the Pattern Formation problem for mobile robots, features such as synchronicity, chirality, and rigidity are computationally irrelevant.

The Shadows of a Cycle Cannot All Be Paths

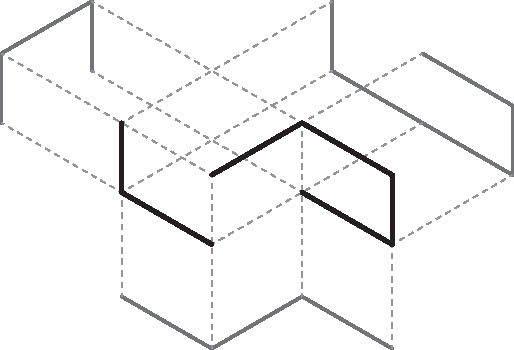
A "shadow" of a subset $S$ of Euclidean space is an orthogonal projection of $S$ into one of the coordinate hyperplanes. In this paper we show that it is not possible for all three shadows of a cycle (i.e., a simple closed curve) in $\mathbb R^3$ to be paths (i.e., simple open curves). We also show two contrasting results: the three shadows of a path in $\mathbb R^3$ can all be cycles (although not all convex) and, for every $d\geq 1$, there exists a $d$-sphere embedded in $\mathbb R^{d+2}$ whose $d+2$ shadows have no holes (i.e., they deformation-retract onto a point).

Getting Close Without Touching: Near-Gathering for Autonomous Mobile Robots

In this paper we study the Near-Gathering problem for a finite set of dimensionless, deterministic, asynchronous, anonymous, oblivious and autonomous mobile robots with limited visibility moving in the Euclidean plane in Look-Compute-Move (LCM) cycles. In this problem, the robots have to get close enough to each other, so that every robot can see all the others, without touching (i.e., colliding with) any other robot. The importance of solving the Near-Gathering problem is that it makes it possible to overcome the restriction of having robots with limited visibility. Hence it allows to exploit all the studies (the majority, actually) done on this topic in the unlimited visibility setting. Indeed, after the robots get close enough to each other, they are able to see all the robots in the system, a scenario that is similar to the one where the robots have unlimited visibility. We present the first (deterministic) algorithm for the Near-Gathering problem, to the best of our knowledge, which allows a set of autonomous mobile robots to nearly gather within finite time without ever colliding. Our algorithm assumes some reasonable conditions on the input configuration (the Near-Gathering problem is easily seen to be unsolvable in general). Further, all the robots are assumed to have a compass (hence they agree on the "North" direction), but they do not necessarily have the same handedness (hence they may disagree on the clockwise direction). We also show how the robots can detect termination, i.e., detect when the Near-Gathering problem has been solved. This is crucial when the robots have to perform a generic task after having nearly gathered. We show that termination detection can be obtained even if the total number of robots is unknown to the robots themselves (i.e., it is not a parameter of the algorithm), and robots have no way to explicitly communicate.

Rendezvous of Two Robots with Constant Memory

We study the impact that persistent memory has on the classical rendezvous problem of two mobile computational entities, called robots, in the plane. It is well known that, without additional assumptions, rendezvous is impossible if the entities are oblivious (i.e., have no persistent memory) even if the system is semi-synchronous (SSynch). It has been recently shown that rendezvous is possible even if the system is asynchronous (ASynch) if each robot is endowed with O(1) bits of persistent memory, can transmit O(1) bits in each cycle, and can remember (i.e., can persistently store) the last received transmission. This setting is overly powerful. In this paper we weaken that setting in two different ways: (1) by maintaining the O(1) bits of persistent memory but removing the communication capabilities; and (2) by maintaining the O(1) transmission capability and the ability to remember the last received transmission, but removing the ability of an agent to remember its previous activities. We call the former setting finite-state (FState) and the latter finite-communication (FComm). Note that, even though its use is very different, in both settings, the amount of persistent memory of a robot is constant. We investigate the rendezvous problem in these two weaker settings. We model both settings as a system of robots endowed with visible lights: in FState, a robot can only see its own light, while in FComm a robot can only see the other robot's light. We prove, among other things, that finite-state robots can rendezvous in SSynch, and that finite-communication robots are able to rendezvous even in ASynch. All proofs are constructive: in each setting, we present a protocol that allows the two robots to rendezvous in finite time.

Rendezvous of two robots with visible bits

We study the rendezvous problem for two robots moving in the plane (or on a line). Robots are autonomous, anonymous, oblivious, and carry colored lights that are visible to both. We consider deterministic distributed algorithms in which robots do not use distance information, but try to reduce (or increase) their distance by a constant factor, depending on their lights' colors. We give a complete characterization of the number of colors that are necessary to solve the rendezvous problem in every possible model, ranging from fully synchronous to semi-synchronous to asynchronous, rigid and non-rigid, with preset or arbitrary initial configuration. In particular, we show that three colors are sufficient in the non-rigid asynchronous model with arbitrary initial configuration. In contrast, two colors are insufficient in the rigid asynchronous model with arbitrary initial configuration and in the non-rigid asynchronous model with preset initial configuration. Additionally, if the robots are able to distinguish between zero and non-zero distances, we show how they can solve rendezvous and detect termination using only three colors, even in the non-rigid asynchronous model with arbitrary initial configuration.