The Shadows of a Cycle Cannot All Be Paths
Paper and Code
Jul 09, 2015

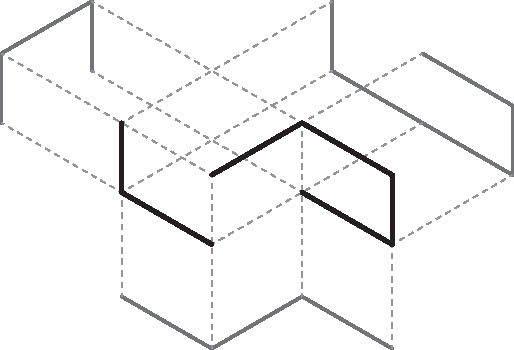

A "shadow" of a subset $S$ of Euclidean space is an orthogonal projection of $S$ into one of the coordinate hyperplanes. In this paper we show that it is not possible for all three shadows of a cycle (i.e., a simple closed curve) in $\mathbb R^3$ to be paths (i.e., simple open curves). We also show two contrasting results: the three shadows of a path in $\mathbb R^3$ can all be cycles (although not all convex) and, for every $d\geq 1$, there exists a $d$-sphere embedded in $\mathbb R^{d+2}$ whose $d+2$ shadows have no holes (i.e., they deformation-retract onto a point).
* 6 pages, 10 figures
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge