Rendezvous and Merging for Two Metamorphic Robotic Systems without Global Compass

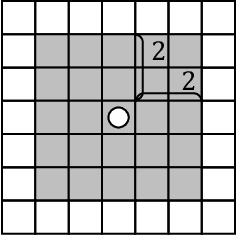
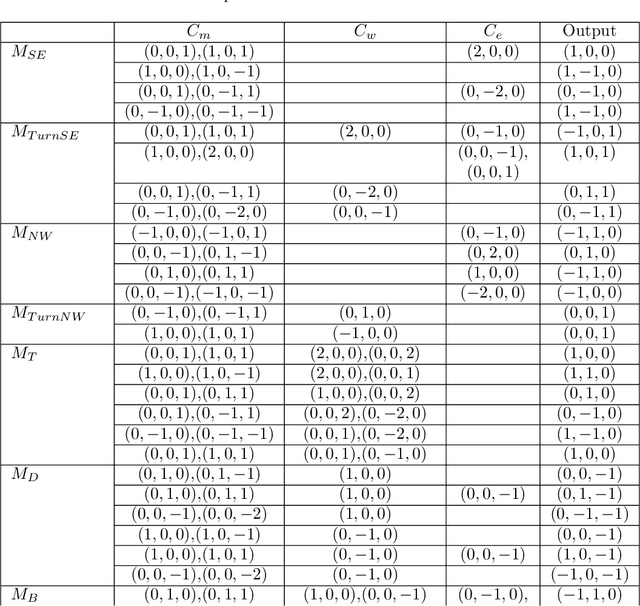
A metamorphic robotic system (MRS) consists of anonymous modules, each of which autonomously moves in the 2D square grid by sliding and rotation with keeping connectivity among the modules. Existing literature considers distributed coordination among modules so that they collectively form a single MRS. In this paper, we consider distributed coordination for two MRSs. We first present a rendezvous algorithm that makes the two MRSs gather so that each module can observe all the other modules. Then, we present a merge algorithm that makes the two MRSs assemble and establish connectivity after rendezvous is finished. These two algorithms assume that each MRS consists of five modules, that do not have a common coordinate system. Finally, we show that five modules for each MRS is necessary to solve the rendezvous problem. To the best of our knowledge, our result is the first result on distributed coordination of multiple MRSs.

Search by a Metamorphic Robotic System in a Finite 3D Cubic Grid

We consider search in a finite 3D cubic grid by a metamorphic robotic system (MRS), that consists of anonymous modules. A module can perform a sliding and rotation while the whole modules keep connectivity. As the number of modules increases, the variety of actions that the MRS can perform increases. The search problem requires the MRS to find a target in a given finite field. Doi et al. (SSS 2018) demonstrate a necessary and sufficient number of modules for search in a finite 2D square grid. We consider search in a finite 3D cubic grid and investigate the effect of common knowledge. We consider three different settings. First, we show that three modules are necessary and sufficient when all modules are equipped with a common compass, i.e., they agree on the direction and orientation of the $x$, $y$, and $z$ axes. Second, we show that four modules are necessary and sufficient when all modules agree on the direction and orientation of the vertical axis. Finally, we show that five modules are necessary and sufficient when all modules are not equipped with a common compass. Our results show that the shapes of the MRS in the 3D cubic grid have richer structure than those in the 2D square grid.

Synchronization by Asynchronous Mobile Robots with Limited Visibility

A mobile robot system consists of anonymous mobile robots, each of which autonomously performs sensing, computation, and movement according to a common algorithm, so that the robots collectively achieve a given task. There are two main models of time and activation of the robots. In the semi-synchronous model (SSYNC), the robots share a common notion of time; at each time unit, a subset of the robots is activated, and each performs all three actions (sensing, computation, and movement) in that time unit. In the asynchronous model (ASYNC), there is no common notion of time, the robots are activated at arbitrary times, and the duration of each action is arbitrary but finite. In this paper, we investigate the problem of synchronizing ASNYC robots with limited sensing range, i.e., limited visibility. We first present a sufficient condition for an ASYNC execution of a common algorithm ${\cal A}$ to have a corresponding SSYNC execution of ${\cal A}$; our condition imposes timing constraints on the activation schedule of the robots and visibility constraints during movement. Then, we prove that this condition is necessary (with probability $1$) under a randomized ASYNC adversary. Finally, we present a synchronization algorithm for luminous ASYNC robots with limited visibility, each equipped with a light that can take a constant number of colors. Our algorithm enables luminous ASYNC robots to simulate any algorithm ${\cal A}$, designed for the (non-luminous) SSYNC robots and satisfying visibility constraints.

Gathering on a Circle with Limited Visibility by Anonymous Oblivious Robots

A swarm of anonymous oblivious mobile robots, operating in deterministic Look-Compute-Move cycles, is confined within a circular track. All robots agree on the clockwise direction (chirality), they are activated by an adversarial semi-synchronous scheduler (SSYNCH), and an active robot always reaches the destination point it computes (rigidity). Robots have limited visibility: each robot can see only the points on the circle that have an angular distance strictly smaller than a constant $\vartheta$ from the robot's current location, where $0<\vartheta\leq\pi$ (angles are expressed in radians). We study the Gathering problem for such a swarm of robots: that is, all robots are initially in distinct locations on the circle, and their task is to reach the same point on the circle in a finite number of turns, regardless of the way they are activated by the scheduler. Note that, due to the anonymity of the robots, this task is impossible if the initial configuration is rotationally symmetric; hence, we have to make the assumption that the initial configuration be rotationally asymmetric. We prove that, if $\vartheta=\pi$ (i.e., each robot can see the entire circle except its antipodal point), there is a distributed algorithm that solves the Gathering problem for swarms of any size. By contrast, we also prove that, if $\vartheta\leq \pi/2$, no distributed algorithm solves the Gathering problem, regardless of the size of the swarm, even under the assumption that the initial configuration is rotationally asymmetric and the visibility graph of the robots is connected. The latter impossibility result relies on a probabilistic technique based on random perturbations, which is novel in the context of anonymous mobile robots. Such a technique is of independent interest, and immediately applies to other Pattern-Formation problems.

Network Creation Games with Local Information and Edge Swaps

In the swap game (SG) selfish players, each of which is associated to a vertex, form a graph by edge swaps, i.e., a player changes its strategy by simultaneously removing an adjacent edge and forming a new edge (Alon et al., 2013). The cost of a player considers the average distance to all other players or the maximum distance to other players. Any SG by $n$ players starting from a tree converges to an equilibrium with a constant Price of Anarchy (PoA) within $O(n^3)$ edge swaps (Lenzner, 2011). We focus on SGs where each player knows the subgraph induced by players within distance $k$. Therefore, each player cannot compute its cost nor a best response. We first consider pessimistic players who consider the worst-case global graph. We show that any SG starting from a tree (i) always converges to an equilibrium within $O(n^3)$ edge swaps irrespective of the value of $k$, (ii) the PoA is $\Theta(n)$ for $k=1,2,3$, and (iii) the PoA is constant for $k \geq 4$. We then introduce weakly pessimistic players and optimistic players and show that these less pessimistic players achieve constant PoA for $k \leq 3$ at the cost of best response cycles.

Exploration of Finite 2D Square Grid by a Metamorphic Robotic System

We consider exploration of finite 2D square grid by a metamorphic robotic system consisting of anonymous oblivious modules. The number of possible shapes of a metamorphic robotic system grows as the number of modules increases. The shape of the system serves as its memory and shows its functionality. We consider the effect of global compass on the minimum number of modules necessary to explore a finite 2D square grid. We show that if the modules agree on the directions (north, south, east, and west), three modules are necessary and sufficient for exploration from an arbitrary initial configuration, otherwise five modules are necessary and sufficient for restricted initial configurations.

Shape Formation by Programmable Particles

Shape formation is a basic distributed problem for systems of computational mobile entities. Intensively studied for systems of autonomous mobile robots, it has recently been investigated in the realm of programmable matter. Namely, it has been studied in the geometric Amoebot model, where the anonymous entities, called particles, operate on a hexagonal tessellation of the plane and have limited computational power (they have constant memory), strictly local interaction and communication capabilities (only with particles in neighboring nodes of the grid), and limited motorial capabilities (from a grid node to an empty neighboring node); their activation is controlled by an adversarial scheduler. Recent investigations have shown how, starting from a well-structured configuration in which the particles form a (not necessarily complete) triangle, the particles can form a large class of shapes. This result has been established under several assumptions: agreement on the clockwise direction (i.e., chirality), a sequential activation schedule, and randomization (i.e., particles can flip coins). In this paper we provide a characterization of which shapes can be formed deterministically starting from any simply connected initial configuration of $n$ particles. As a byproduct, if randomization is allowed, then any input shape can be formed from any initial (simply connected) shape by our algorithm, provided that $n$ is large enough. Our algorithm works without chirality, proving that chirality is computationally irrelevant for shape formation. Furthermore, it works under a strong adversarial scheduler, not necessarily sequential. We also consider the complexity of shape formation in terms of both the number of rounds and of moves performed by the particles. We prove that our solution has a complexity of $O(n^2)$ rounds and moves: this number of moves is also asymptotically optimal.

Plane Formation by Synchronous Mobile Robots in the Three Dimensional Euclidean Space

Creating a swarm of mobile computing entities frequently called robots, agents or sensor nodes, with self-organization ability is a contemporary challenge in distributed computing. Motivated by this, we investigate the plane formation problem that requires a swarm of robots moving in the three dimensional Euclidean space to land on a common plane. The robots are fully synchronous and endowed with visual perception. But they do not have identifiers, nor access to the global coordinate system, nor any means of explicit communication with each other. Though there are plenty of results on the agreement problem for robots in the two dimensional plane, for example, the point formation problem, the pattern formation problem, and so on, this is the first result for robots in the three dimensional space. This paper presents a necessary and sufficient condition for fully-synchronous robots to solve the plane formation problem that does not depend on obliviousness i.e., the availability of local memory at robots. An implication of the result is somewhat counter-intuitive: The robots cannot form a plane from most of the semi-regular polyhedra, while they can form a plane from every regular polyhedron (except a regular icosahedron), whose symmetry is usually considered to be higher than any semi-regular polyhedrdon.