Rendezvous and Merging for Two Metamorphic Robotic Systems without Global Compass

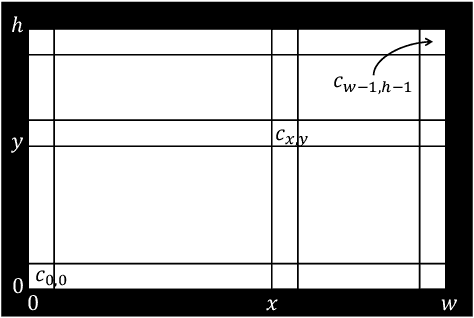
A metamorphic robotic system (MRS) consists of anonymous modules, each of which autonomously moves in the 2D square grid by sliding and rotation with keeping connectivity among the modules. Existing literature considers distributed coordination among modules so that they collectively form a single MRS. In this paper, we consider distributed coordination for two MRSs. We first present a rendezvous algorithm that makes the two MRSs gather so that each module can observe all the other modules. Then, we present a merge algorithm that makes the two MRSs assemble and establish connectivity after rendezvous is finished. These two algorithms assume that each MRS consists of five modules, that do not have a common coordinate system. Finally, we show that five modules for each MRS is necessary to solve the rendezvous problem. To the best of our knowledge, our result is the first result on distributed coordination of multiple MRSs.

Search by a Metamorphic Robotic System in a Finite 3D Cubic Grid

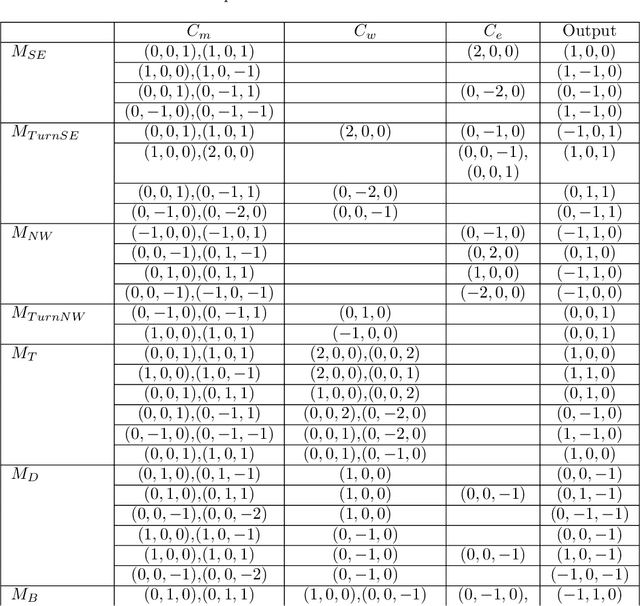
We consider search in a finite 3D cubic grid by a metamorphic robotic system (MRS), that consists of anonymous modules. A module can perform a sliding and rotation while the whole modules keep connectivity. As the number of modules increases, the variety of actions that the MRS can perform increases. The search problem requires the MRS to find a target in a given finite field. Doi et al. (SSS 2018) demonstrate a necessary and sufficient number of modules for search in a finite 2D square grid. We consider search in a finite 3D cubic grid and investigate the effect of common knowledge. We consider three different settings. First, we show that three modules are necessary and sufficient when all modules are equipped with a common compass, i.e., they agree on the direction and orientation of the $x$, $y$, and $z$ axes. Second, we show that four modules are necessary and sufficient when all modules agree on the direction and orientation of the vertical axis. Finally, we show that five modules are necessary and sufficient when all modules are not equipped with a common compass. Our results show that the shapes of the MRS in the 3D cubic grid have richer structure than those in the 2D square grid.