Separating Bounded and Unbounded Asynchrony for Autonomous Robots: Point Convergence with Limited Visibility

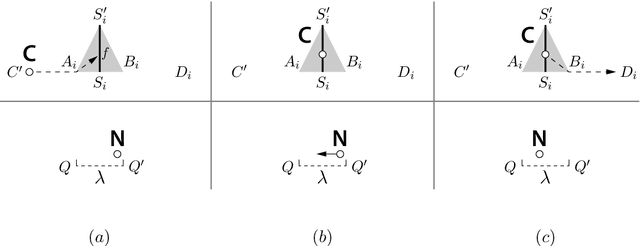
Among fundamental problems in the context of distributed computing by autonomous mobile entities, one of the most representative and well studied is {\sc Point Convergence}: given an arbitrary initial configuration of identical entities, disposed in the Euclidean plane, move in such a way that, for all $\eps>0$, a configuration in which the separation between all entities is at most $\eps$ is eventually reached and maintained. The problem has been previously studied in a variety of settings, including full visibility, exact measurements (like distances and angles), and synchronous activation of entities. Our study concerns the minimal assumptions under which entities, moving asynchronously with limited and unknown visibility range and subject to limited imprecision in measurements, can be guaranteed to converge in this way. We present an algorithm that solves {\sc Point Convergence}, for entities in the plane, in such a setting, provided the degree of asynchrony is bounded: while any one entity is active, any other entity can be activated at most $k$ times, for some arbitrarily large but fixed $k$. This provides a strong positive answer to a decade old open question posed by Katreniak. We also prove that in a comparable setting that permits unbounded asynchrony, {\sc Point Convergence} in the plane is impossible, contingent on the natural assumption that algorithms maintain the (visible) connectivity among entities present in the initial configuration. This variant, that we call {\sc Cohesive Convergence}, serves to distinguish the power of bounded and unbounded asynchrony in the control of autonomous mobile entities, settling at the same time a long-standing question whether in the Euclidean plane synchronously scheduled entities are more powerful than asynchronously scheduled entities.

Synchronization by Asynchronous Mobile Robots with Limited Visibility

A mobile robot system consists of anonymous mobile robots, each of which autonomously performs sensing, computation, and movement according to a common algorithm, so that the robots collectively achieve a given task. There are two main models of time and activation of the robots. In the semi-synchronous model (SSYNC), the robots share a common notion of time; at each time unit, a subset of the robots is activated, and each performs all three actions (sensing, computation, and movement) in that time unit. In the asynchronous model (ASYNC), there is no common notion of time, the robots are activated at arbitrary times, and the duration of each action is arbitrary but finite. In this paper, we investigate the problem of synchronizing ASNYC robots with limited sensing range, i.e., limited visibility. We first present a sufficient condition for an ASYNC execution of a common algorithm ${\cal A}$ to have a corresponding SSYNC execution of ${\cal A}$; our condition imposes timing constraints on the activation schedule of the robots and visibility constraints during movement. Then, we prove that this condition is necessary (with probability $1$) under a randomized ASYNC adversary. Finally, we present a synchronization algorithm for luminous ASYNC robots with limited visibility, each equipped with a light that can take a constant number of colors. Our algorithm enables luminous ASYNC robots to simulate any algorithm ${\cal A}$, designed for the (non-luminous) SSYNC robots and satisfying visibility constraints.

Oblivious Permutations on the Plane

We consider a distributed system of n identical mobile robots operating in the two dimensional Euclidian plane. As in the previous studies, we consider the robots to be anonymous, oblivious, dis-oriented, and without any communication capabilities, operating based on the Look-Compute-Move model where the next location of a robot depends only on its view of the current configuration. Even in this seemingly weak model, most formation problems which require constructing specific configurations, can be solved quite easily when the robots are fully synchronized with each other. In this paper we introduce and study a new class of problems which, unlike the formation problems so far, cannot always be solved even in the fully synchronous model with atomic and rigid moves. This class of problems requires the robots to permute their locations in the plane. In particular, we are interested in implementing two special types of permutations -- permutations without any fixed points and permutations of order $n$. The former (called MOVE-ALL) requires each robot to visit at least two of the initial locations, while the latter (called VISIT-ALL) requires every robot to visit each of the initial locations in a periodic manner. We provide a characterization of the solvability of these problems, showing the main challenges in solving this class of problems for mobile robots. We also provide algorithms for the feasible cases, in particular distinguishing between one-step algorithms (where each configuration must be a permutation of the original configuration) and multi-step algorithms (which allow intermediate configurations). These results open a new research direction in mobile distributed robotics which has not been investigated before.

TuringMobile: A Turing Machine of Oblivious Mobile Robots with Limited Visibility and its Applications

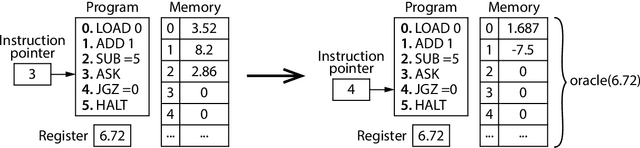
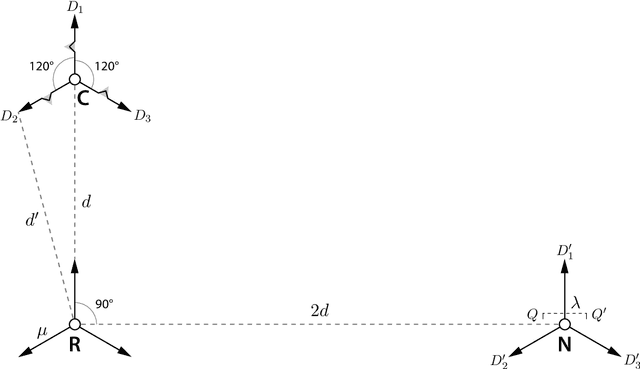
In this paper we investigate the computational power of a set of mobile robots with limited visibility. At each iteration, a robot takes a snapshot of its surroundings, uses the snapshot to compute a destination point, and it moves toward its destination. Each robot is punctiform and memoryless, it operates in $\mathbb{R}^m$, it has a local reference system independent of the other robots' ones, and is activated asynchronously by an adversarial scheduler. Moreover, robots are non-rigid, in that they may be stopped by the scheduler at each move before reaching their destination (but are guaranteed to travel at least a fixed unknown distance before being stopped). We show that despite these strong limitations, it is possible to arrange $3m+3k$ of these weak entities in $\mathbb{R}^m$ to simulate the behavior of a stronger robot that is rigid (i.e., it always reaches its destination) and is endowed with $k$ registers of persistent memory, each of which can store a real number. We call this arrangement a TuringMobile. In its simplest form, a TuringMobile consisting of only three robots can travel in the plane and store and update a single real number. We also prove that this task is impossible with fewer than three robots. Among the applications of the TuringMobile, we focused on Near-Gathering (all robots have to gather in a small-enough disk) and Pattern Formation (of which Gathering is a special case) with limited visibility. Interestingly, our investigation implies that both problems are solvable in Euclidean spaces of any dimension, even if the visibility graph of the robots is initially disconnected, provided that a small amount of these robots are arranged to form a TuringMobile. In the special case of the plane, a basic TuringMobile of only three robots is sufficient.

Meeting in a Polygon by Anonymous Oblivious Robots

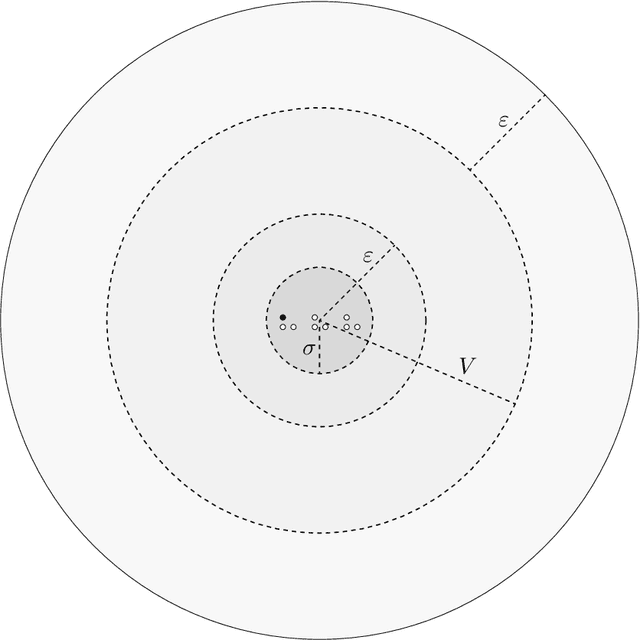
The Meeting problem for $k\geq 2$ searchers in a polygon $P$ (possibly with holes) consists in making the searchers move within $P$, according to a distributed algorithm, in such a way that at least two of them eventually come to see each other, regardless of their initial positions. The polygon is initially unknown to the searchers, and its edges obstruct both movement and vision. Depending on the shape of $P$, we minimize the number of searchers $k$ for which the Meeting problem is solvable. Specifically, if $P$ has a rotational symmetry of order $\sigma$ (where $\sigma=1$ corresponds to no rotational symmetry), we prove that $k=\sigma+1$ searchers are sufficient, and the bound is tight. Furthermore, we give an improved algorithm that optimally solves the Meeting problem with $k=2$ searchers in all polygons whose barycenter is not in a hole (which includes the polygons with no holes). Our algorithms can be implemented in a variety of standard models of mobile robots operating in Look-Compute-Move cycles. For instance, if the searchers have memory but are anonymous, asynchronous, and have no agreement on a coordinate system or a notion of clockwise direction, then our algorithms work even if the initial memory contents of the searchers are arbitrary and possibly misleading. Moreover, oblivious searchers can execute our algorithms as well, encoding information by carefully positioning themselves within the polygon. This code is computable with basic arithmetic operations, and each searcher can geometrically construct its own destination point at each cycle using only a compass. We stress that such memoryless searchers may be located anywhere in the polygon when the execution begins, and hence the information they initially encode is arbitrary. Our algorithms use a self-stabilizing map construction subroutine which is of independent interest.

Shape Formation by Programmable Particles

Shape formation is a basic distributed problem for systems of computational mobile entities. Intensively studied for systems of autonomous mobile robots, it has recently been investigated in the realm of programmable matter. Namely, it has been studied in the geometric Amoebot model, where the anonymous entities, called particles, operate on a hexagonal tessellation of the plane and have limited computational power (they have constant memory), strictly local interaction and communication capabilities (only with particles in neighboring nodes of the grid), and limited motorial capabilities (from a grid node to an empty neighboring node); their activation is controlled by an adversarial scheduler. Recent investigations have shown how, starting from a well-structured configuration in which the particles form a (not necessarily complete) triangle, the particles can form a large class of shapes. This result has been established under several assumptions: agreement on the clockwise direction (i.e., chirality), a sequential activation schedule, and randomization (i.e., particles can flip coins). In this paper we provide a characterization of which shapes can be formed deterministically starting from any simply connected initial configuration of $n$ particles. As a byproduct, if randomization is allowed, then any input shape can be formed from any initial (simply connected) shape by our algorithm, provided that $n$ is large enough. Our algorithm works without chirality, proving that chirality is computationally irrelevant for shape formation. Furthermore, it works under a strong adversarial scheduler, not necessarily sequential. We also consider the complexity of shape formation in terms of both the number of rounds and of moves performed by the particles. We prove that our solution has a complexity of $O(n^2)$ rounds and moves: this number of moves is also asymptotically optimal.

Rendezvous of Two Robots with Constant Memory

We study the impact that persistent memory has on the classical rendezvous problem of two mobile computational entities, called robots, in the plane. It is well known that, without additional assumptions, rendezvous is impossible if the entities are oblivious (i.e., have no persistent memory) even if the system is semi-synchronous (SSynch). It has been recently shown that rendezvous is possible even if the system is asynchronous (ASynch) if each robot is endowed with O(1) bits of persistent memory, can transmit O(1) bits in each cycle, and can remember (i.e., can persistently store) the last received transmission. This setting is overly powerful. In this paper we weaken that setting in two different ways: (1) by maintaining the O(1) bits of persistent memory but removing the communication capabilities; and (2) by maintaining the O(1) transmission capability and the ability to remember the last received transmission, but removing the ability of an agent to remember its previous activities. We call the former setting finite-state (FState) and the latter finite-communication (FComm). Note that, even though its use is very different, in both settings, the amount of persistent memory of a robot is constant. We investigate the rendezvous problem in these two weaker settings. We model both settings as a system of robots endowed with visible lights: in FState, a robot can only see its own light, while in FComm a robot can only see the other robot's light. We prove, among other things, that finite-state robots can rendezvous in SSynch, and that finite-communication robots are able to rendezvous even in ASynch. All proofs are constructive: in each setting, we present a protocol that allows the two robots to rendezvous in finite time.

Expressivity of Time-Varying Graphs and the Power of Waiting in Dynamic Networks

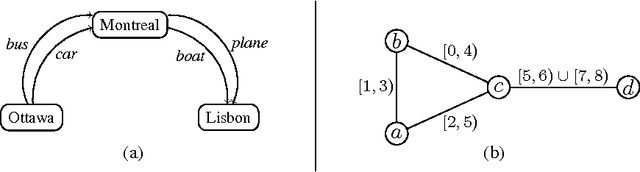
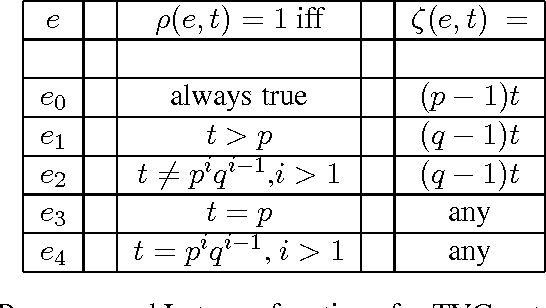
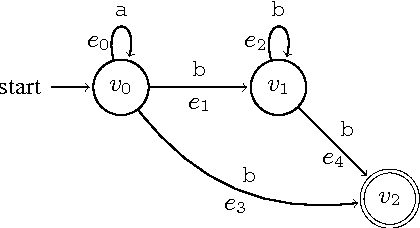
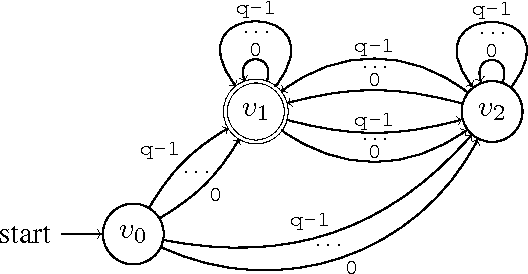
In infrastructure-less highly dynamic networks, computing and performing even basic tasks (such as routing and broadcasting) is a very challenging activity due to the fact that connectivity does not necessarily hold, and the network may actually be disconnected at every time instant. Clearly the task of designing protocols for these networks is less difficult if the environment allows waiting (i.e., it provides the nodes with store-carry-forward-like mechanisms such as local buffering) than if waiting is not feasible. No quantitative corroborations of this fact exist (e.g., no answer to the question: how much easier?). In this paper, we consider these qualitative questions about dynamic networks, modeled as time-varying (or evolving) graphs, where edges exist only at some times. We examine the difficulty of the environment in terms of the expressivity of the corresponding time-varying graph; that is in terms of the language generated by the feasible journeys in the graph. We prove that the set of languages $L_{nowait}$ when no waiting is allowed contains all computable languages. On the other end, using algebraic properties of quasi-orders, we prove that $L_{wait}$ is just the family of regular languages. In other words, we prove that, when waiting is no longer forbidden, the power of the accepting automaton (difficulty of the environment) drops drastically from being as powerful as a Turing machine, to becoming that of a Finite-State machine. This (perhaps surprisingly large) gap is a measure of the computational power of waiting. We also study bounded waiting; that is when waiting is allowed at a node only for at most $d$ time units. We prove the negative result that $L_{wait[d]} = L_{nowait}$; that is, the expressivity decreases only if the waiting is finite but unpredictable (i.e., under the control of the protocol designer and not of the environment).

Time-Varying Graphs and Social Network Analysis: Temporal Indicators and Metrics

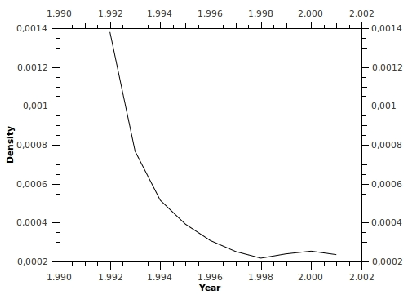
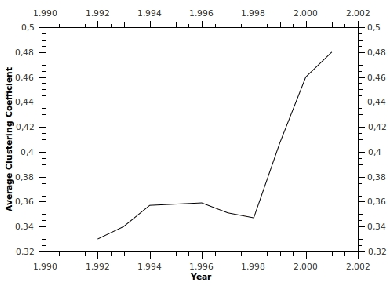
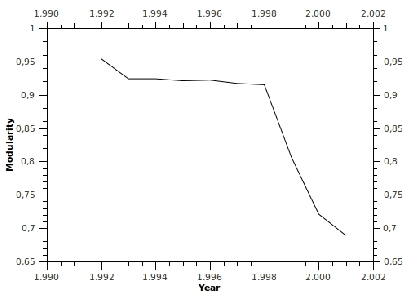
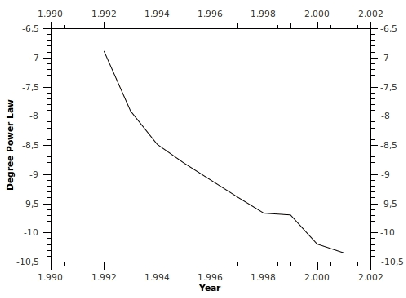
Most instruments - formalisms, concepts, and metrics - for social networks analysis fail to capture their dynamics. Typical systems exhibit different scales of dynamics, ranging from the fine-grain dynamics of interactions (which recently led researchers to consider temporal versions of distance, connectivity, and related indicators), to the evolution of network properties over longer periods of time. This paper proposes a general approach to study that evolution for both atemporal and temporal indicators, based respectively on sequences of static graphs and sequences of time-varying graphs that cover successive time-windows. All the concepts and indicators, some of which are new, are expressed using a time-varying graph formalism.