Expressivity of Time-Varying Graphs and the Power of Waiting in Dynamic Networks

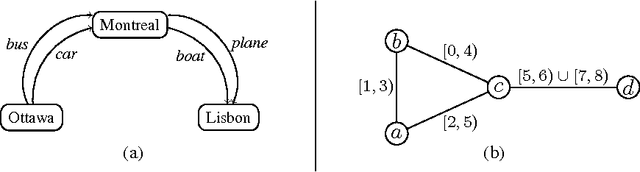
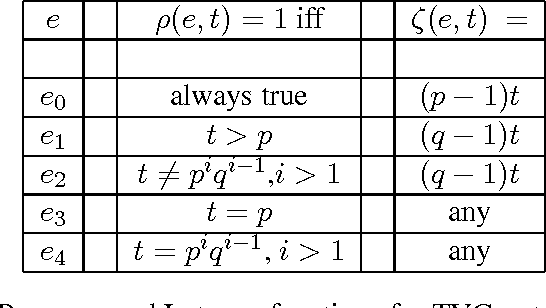
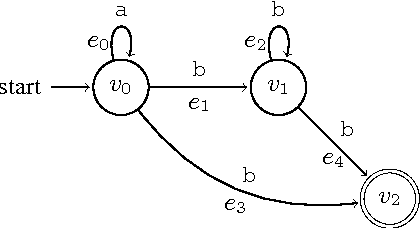
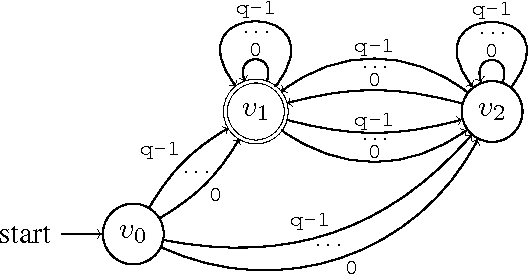
In infrastructure-less highly dynamic networks, computing and performing even basic tasks (such as routing and broadcasting) is a very challenging activity due to the fact that connectivity does not necessarily hold, and the network may actually be disconnected at every time instant. Clearly the task of designing protocols for these networks is less difficult if the environment allows waiting (i.e., it provides the nodes with store-carry-forward-like mechanisms such as local buffering) than if waiting is not feasible. No quantitative corroborations of this fact exist (e.g., no answer to the question: how much easier?). In this paper, we consider these qualitative questions about dynamic networks, modeled as time-varying (or evolving) graphs, where edges exist only at some times. We examine the difficulty of the environment in terms of the expressivity of the corresponding time-varying graph; that is in terms of the language generated by the feasible journeys in the graph. We prove that the set of languages $L_{nowait}$ when no waiting is allowed contains all computable languages. On the other end, using algebraic properties of quasi-orders, we prove that $L_{wait}$ is just the family of regular languages. In other words, we prove that, when waiting is no longer forbidden, the power of the accepting automaton (difficulty of the environment) drops drastically from being as powerful as a Turing machine, to becoming that of a Finite-State machine. This (perhaps surprisingly large) gap is a measure of the computational power of waiting. We also study bounded waiting; that is when waiting is allowed at a node only for at most $d$ time units. We prove the negative result that $L_{wait[d]} = L_{nowait}$; that is, the expressivity decreases only if the waiting is finite but unpredictable (i.e., under the control of the protocol designer and not of the environment).