Rule-based Evolutionary Bayesian Learning

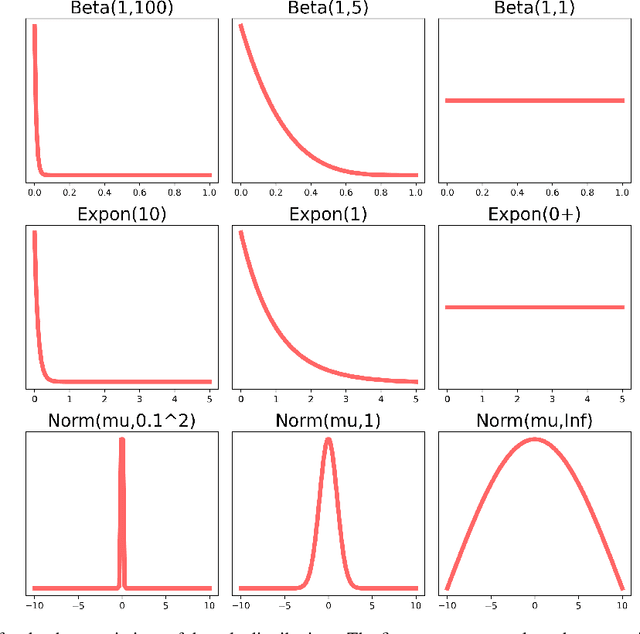
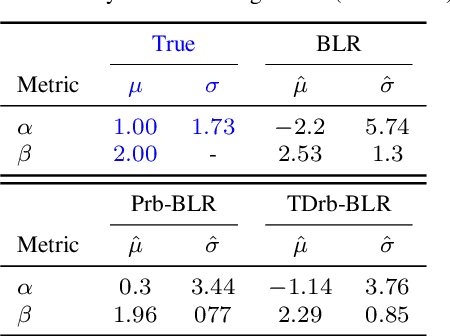
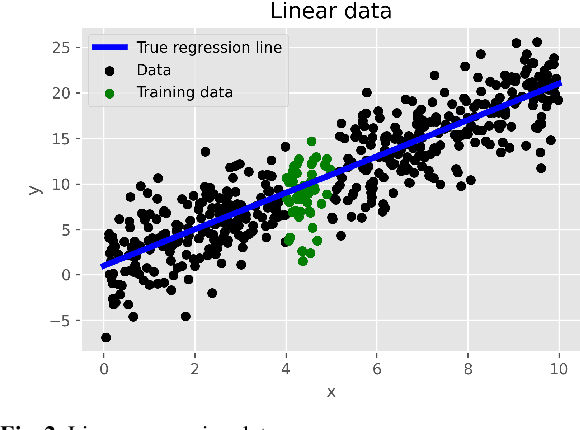
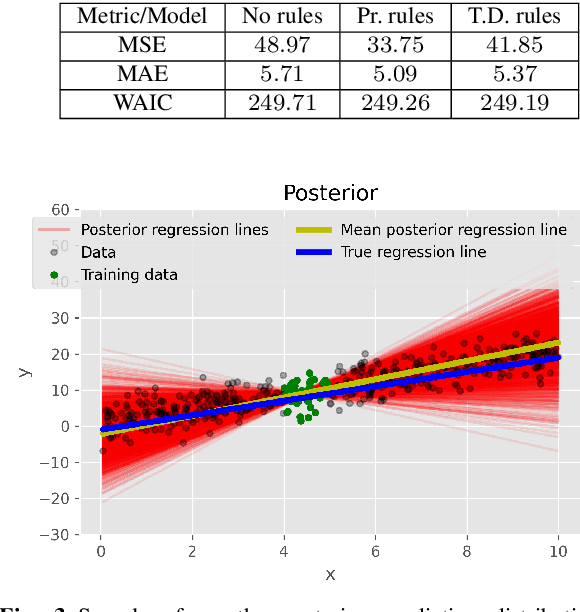
In our previous work, we introduced the rule-based Bayesian Regression, a methodology that leverages two concepts: (i) Bayesian inference, for the general framework and uncertainty quantification and (ii) rule-based systems for the incorporation of expert knowledge and intuition. The resulting method creates a penalty equivalent to a common Bayesian prior, but it also includes information that typically would not be available within a standard Bayesian context. In this work, we extend the aforementioned methodology with grammatical evolution, a symbolic genetic programming technique that we utilise for automating the rules' derivation. Our motivation is that grammatical evolution can potentially detect patterns from the data with valuable information, equivalent to that of expert knowledge. We illustrate the use of the rule-based Evolutionary Bayesian learning technique by applying it to synthetic as well as real data, and examine the results in terms of point predictions and associated uncertainty.

Data-Centric Engineering: integrating simulation, machine learning and statistics. Challenges and Opportunities

Recent advances in machine learning, coupled with low-cost computation, availability of cheap streaming sensors, data storage and cloud technologies, has led to widespread multi-disciplinary research activity with significant interest and investment from commercial stakeholders. Mechanistic models, based on physical equations, and purely data-driven statistical approaches represent two ends of the modelling spectrum. New hybrid, data-centric engineering approaches, leveraging the best of both worlds and integrating both simulations and data, are emerging as a powerful tool with a transformative impact on the physical disciplines. We review the key research trends and application scenarios in the emerging field of integrating simulations, machine learning, and statistics. We highlight the opportunities that such an integrated vision can unlock and outline the key challenges holding back its realisation. We also discuss the bottlenecks in the translational aspects of the field and the long-term upskilling requirements of the existing workforce and future university graduates.

Rule-based Bayesian regression

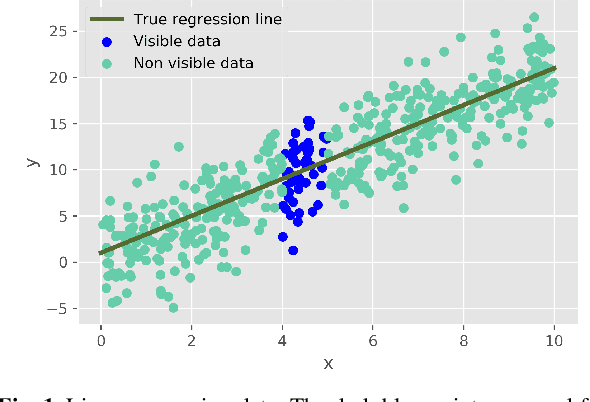
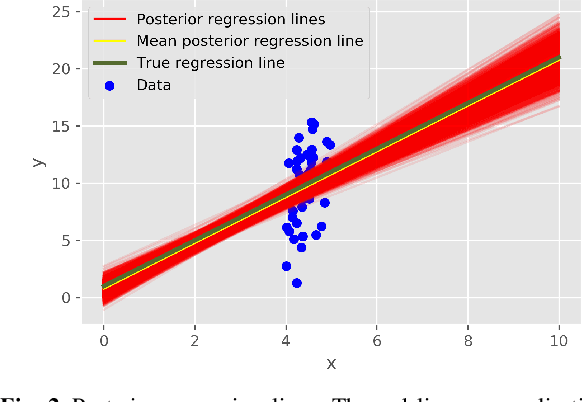
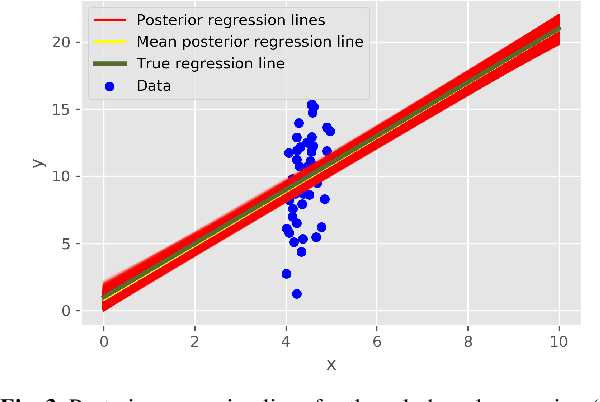
We introduce a novel rule-based approach for handling regression problems. The new methodology carries elements from two frameworks: (i) it provides information about the uncertainty of the parameters of interest using Bayesian inference, and (ii) it allows the incorporation of expert knowledge through rule-based systems. The blending of those two different frameworks can be particularly beneficial for various domains (e.g. engineering), where, even though the significance of uncertainty quantification motivates a Bayesian approach, there is no simple way to incorporate researcher intuition into the model. We validate our models by applying them to synthetic applications: a simple linear regression problem and two more complex structures based on partial differential equations. Finally, we review the advantages of our methodology, which include the simplicity of the implementation, the uncertainty reduction due to the added information and, in some occasions, the derivation of better point predictions, and we address limitations, mainly from the computational complexity perspective, such as the difficulty in choosing an appropriate algorithm and the added computational burden.

Latent-space time evolution of non-intrusive reduced-order models using Gaussian process emulation

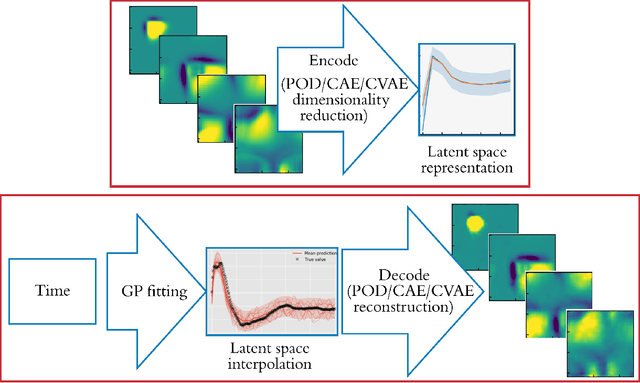
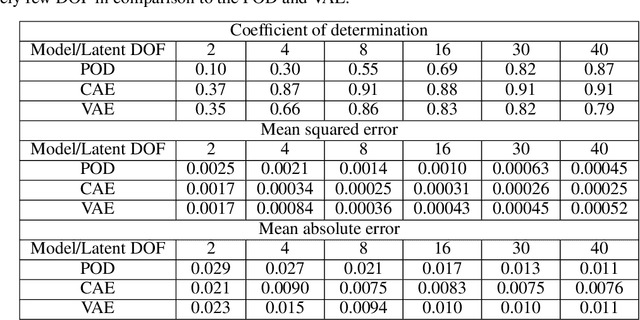
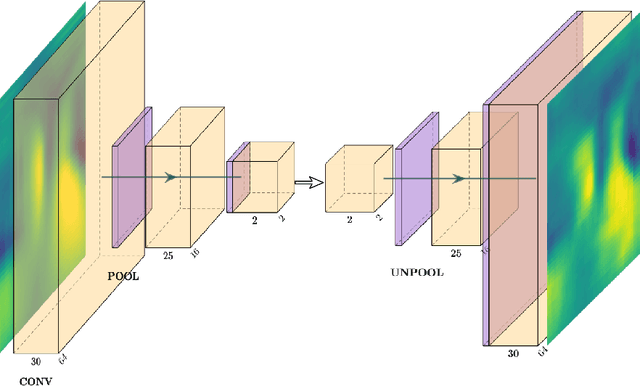
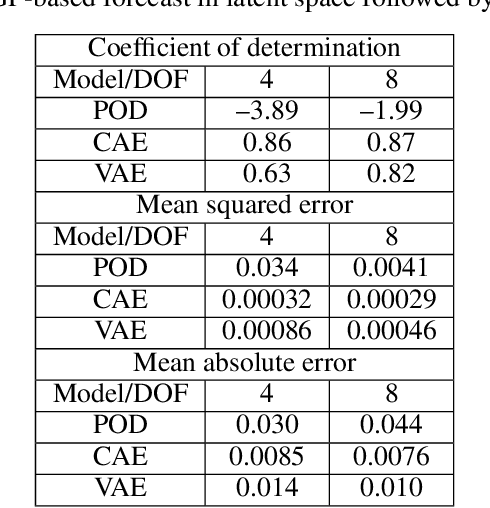
Non-intrusive reduced-order models (ROMs) have recently generated considerable interest for constructing computationally efficient counterparts of nonlinear dynamical systems emerging from various domain sciences. They provide a low-dimensional emulation framework for systems that may be intrinsically high-dimensional. This is accomplished by utilizing a construction algorithm that is purely data-driven. It is no surprise, therefore, that the algorithmic advances of machine learning have led to non-intrusive ROMs with greater accuracy and computational gains. However, in bypassing the utilization of an equation-based evolution, it is often seen that the interpretability of the ROM framework suffers. This becomes more problematic when black-box deep learning methods are used which are notorious for lacking robustness outside the physical regime of the observed data. In this article, we propose the use of a novel latent space interpolation algorithm based on Gaussian process regression. Notably, this reduced-order evolution of the system is parameterized by control parameters to allow for interpolation in space. The use of this procedure also allows for a continuous interpretation of time which allows for temporal interpolation. The latter aspect provides information, with quantified uncertainty, about full-state evolution at a finer resolution than that utilized for training the ROMs. We assess the viability of this algorithm for an advection-dominated system given by the inviscid shallow water equations.

Numerical simulation, clustering and prediction of multi-component polymer precipitation

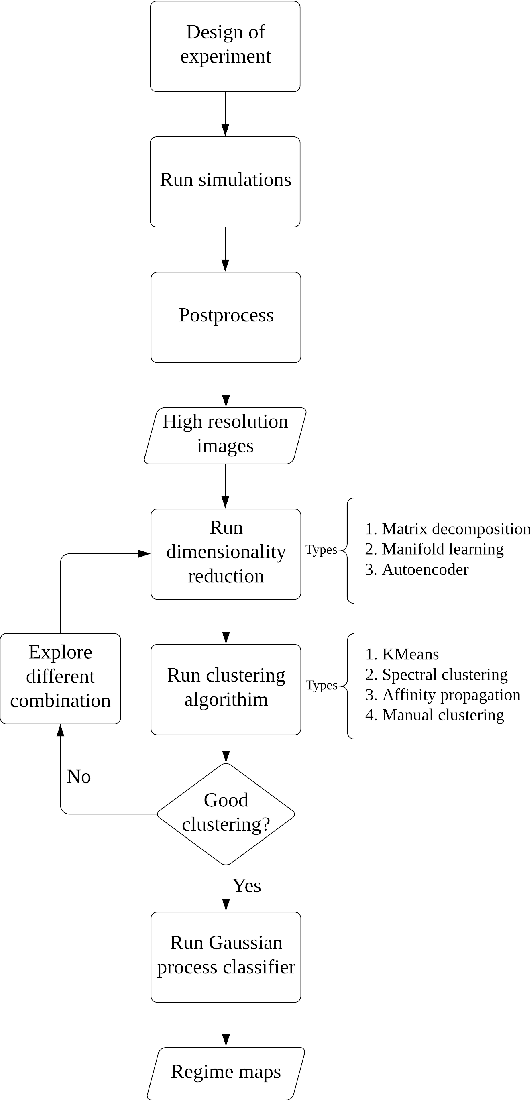
Multi-component polymer systems are of interest in organic photovoltaic and drug delivery applications, among others where diverse morphologies influence performance. An improved understanding of morphology classification, driven by composition-informed prediction tools, will aid polymer engineering practice. We use a modified Cahn-Hilliard model to simulate polymer precipitation. Such physics-based models require high-performance computations that prevent rapid prototyping and iteration in engineering settings. To reduce the required computational costs, we apply machine learning techniques for clustering and consequent prediction of the simulated polymer blend images in conjunction with simulations. Integrating ML and simulations in such a manner reduces the number of simulations needed to map out the morphology of polymer blends as a function of input parameters and also generates a data set which can be used by others to this end. We explore dimensionality reduction, via principal component analysis and autoencoder techniques, and analyse the resulting morphology clusters. Supervised machine learning using Gaussian process classification was subsequently used to predict morphology clusters according to species molar fraction and interaction parameter inputs. Manual pattern clustering yielded the best results, but machine learning techniques were able to predict the morphology of polymer blends with $\geq$ 90 $\%$ accuracy.

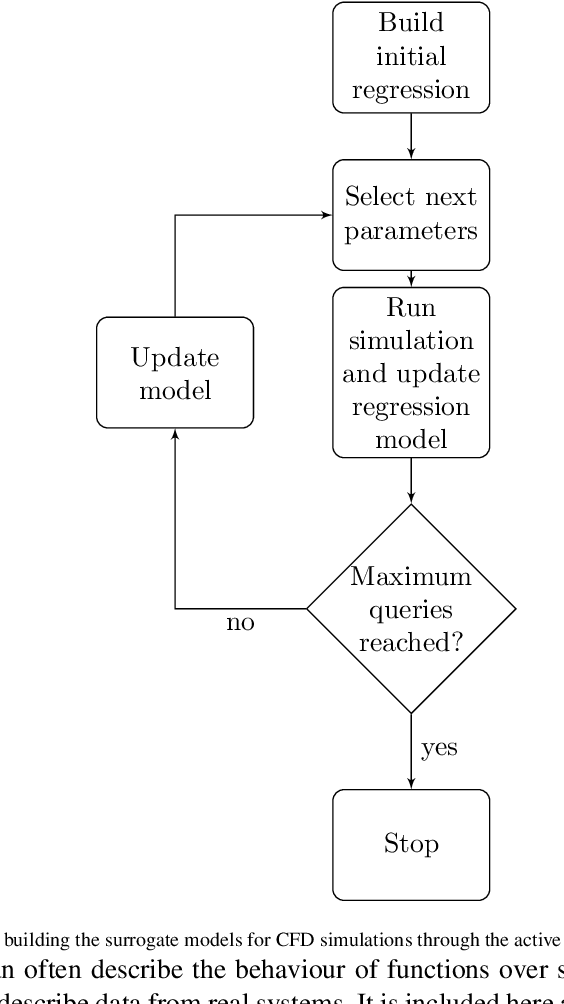
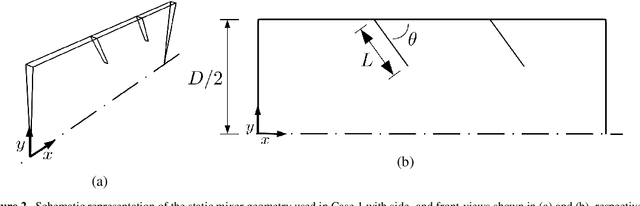
Data-driven surrogate modelling and benchmarking for process equipment

A suite of computational fluid dynamics (CFD) simulations geared towards chemical process equipment modelling has been developed and validated with experimental results from the literature. Various regression based active learning strategies are explored with these CFD simulators in-the-loop under the constraints of a limited function evaluation budget. Specifically, five different sampling strategies and five regression techniques are compared, considering a set of three test cases of industrial significance and varying complexity. Gaussian process regression was observed to have a consistently good performance for these applications. The present quantitative study outlines the pros and cons of the different available techniques and highlights the best practices for their adoption. The test cases and tools are available with an open-source license, to ensure reproducibility and engage the wider research community in contributing to both the CFD models and developing and benchmarking new improved algorithms tailored to this field.

Fuzzy Bayesian Learning

In this paper we propose a novel approach for learning from data using rule based fuzzy inference systems where the model parameters are estimated using Bayesian inference and Markov Chain Monte Carlo (MCMC) techniques. We show the applicability of the method for regression and classification tasks using synthetic data-sets and also a real world example in the financial services industry. Then we demonstrate how the method can be extended for knowledge extraction to select the individual rules in a Bayesian way which best explains the given data. Finally we discuss the advantages and pitfalls of using this method over state-of-the-art techniques and highlight the specific class of problems where this would be useful.

Artificial neural network based modelling approach for municipal solid waste gasification in a fluidized bed reactor

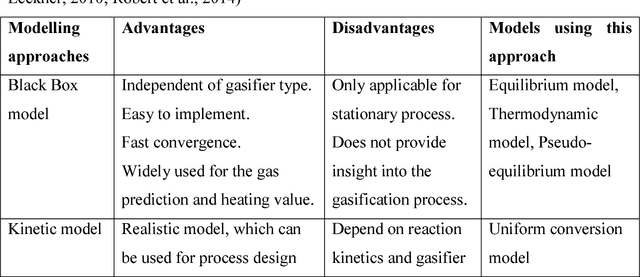
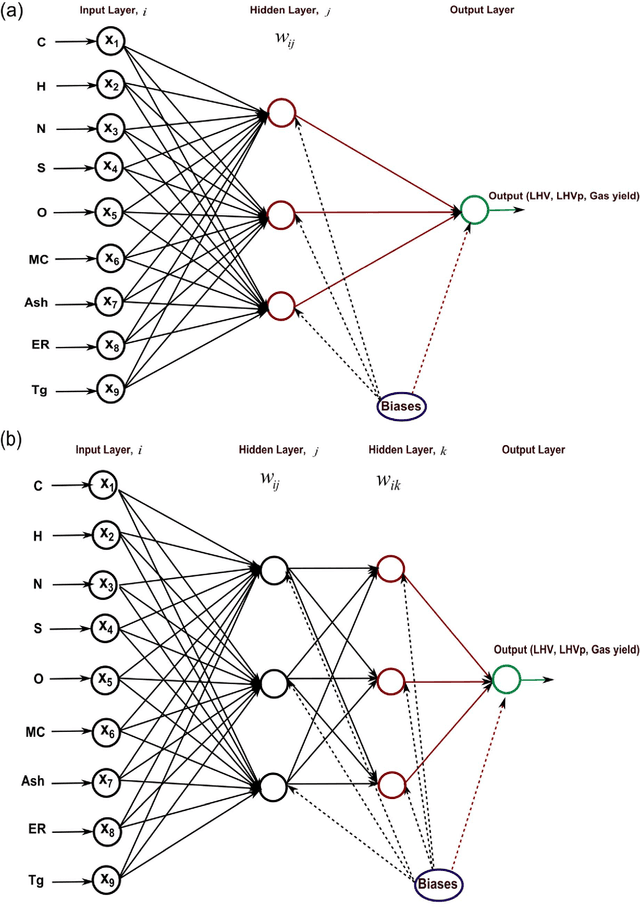
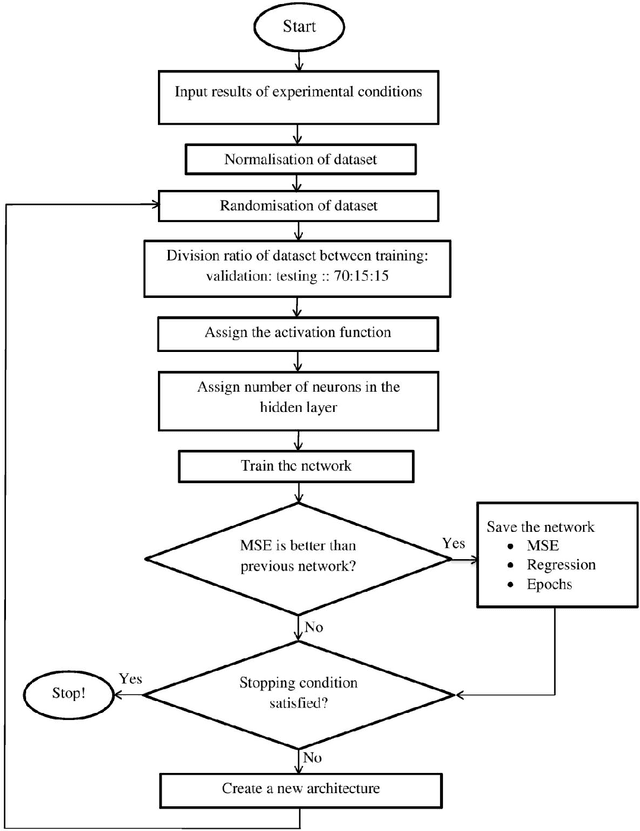
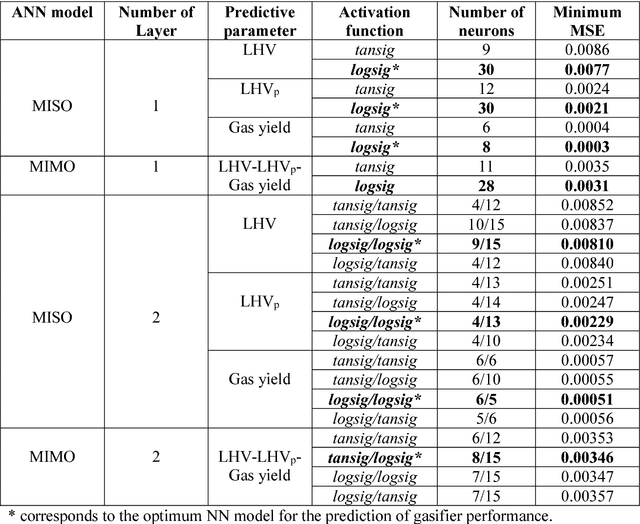
In this paper, multi-layer feed forward neural networks are used to predict the lower heating value of gas (LHV), lower heating value of gasification products including tars and entrained char (LHVp) and syngas yield during gasification of municipal solid waste (MSW) during gasification in a fluidized bed reactor. These artificial neural networks (ANNs) with different architectures are trained using the Levenberg-Marquardt (LM) back-propagation algorithm and a cross validation is also performed to ensure that the results generalise to other unseen datasets. A rigorous study is carried out on optimally choosing the number of hidden layers, number of neurons in the hidden layer and activation function in a network using multiple Monte Carlo runs. Nine input and three output parameters are used to train and test various neural network architectures in both multiple output and single output prediction paradigms using the available experimental datasets. The model selection procedure is carried out to ascertain the best network architecture in terms of predictive accuracy. The simulation results show that the ANN based methodology is a viable alternative which can be used to predict the performance of a fluidized bed gasifier.

Evolving Chaos: Identifying New Attractors of the Generalised Lorenz Family

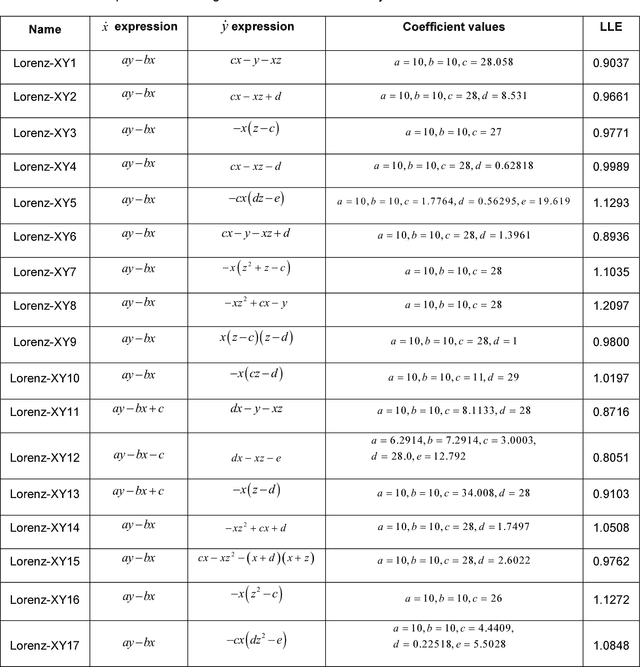
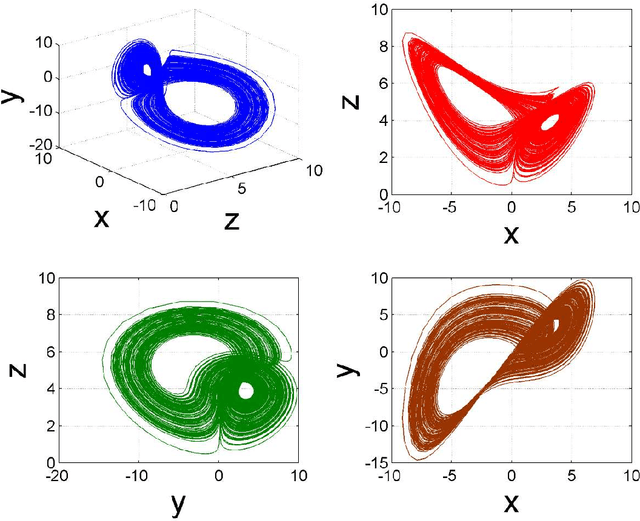
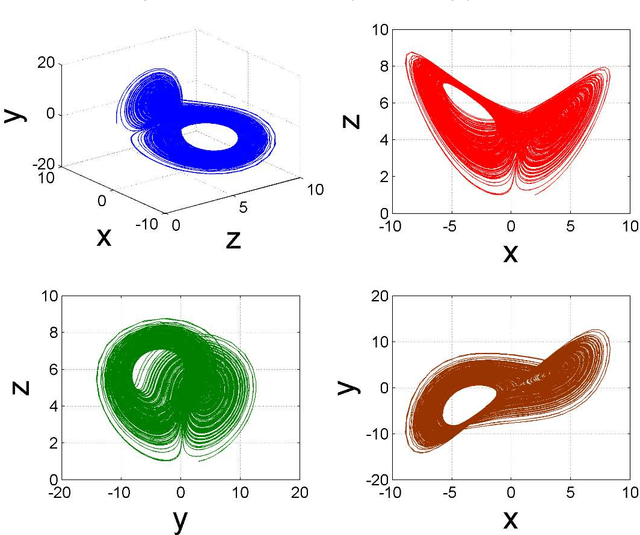
In a recent paper, we presented an intelligent evolutionary search technique through genetic programming (GP) for finding new analytical expressions of nonlinear dynamical systems, similar to the classical Lorenz attractor's which also exhibit chaotic behaviour in the phase space. In this paper, we extend our previous finding to explore yet another gallery of new chaotic attractors which are derived from the original Lorenz system of equations. Compared to the previous exploration with sinusoidal type transcendental nonlinearity, here we focus on only cross-product and higher-power type nonlinearities in the three state equations. We here report over 150 different structures of chaotic attractors along with their one set of parameter values, phase space dynamics and the Largest Lyapunov Exponents (LLE). The expressions of these new Lorenz-like nonlinear dynamical systems have been automatically evolved through multi-gene genetic programming (MGGP). In the past two decades, there have been many claims of designing new chaotic attractors as an incremental extension of the Lorenz family. We provide here a large family of chaotic systems whose structure closely resemble the original Lorenz system but with drastically different phase space dynamics. This advances the state of the art knowledge of discovering new chaotic systems which can find application in many real-world problems. This work may also find its archival value in future in the domain of new chaotic system discovery.

Marginal likelihood based model comparison in Fuzzy Bayesian Learning

In a recent paper [1] we introduced the Fuzzy Bayesian Learning (FBL) paradigm where expert opinions can be encoded in the form of fuzzy rule bases and the hyper-parameters of the fuzzy sets can be learned from data using a Bayesian approach. The present paper extends this work for selecting the most appropriate rule base among a set of competing alternatives, which best explains the data, by calculating the model evidence or marginal likelihood. We explain why this is an attractive alternative over simply minimizing a mean squared error metric of prediction and show the validity of the proposition using synthetic examples and a real world case study in the financial services sector.