Latent-space time evolution of non-intrusive reduced-order models using Gaussian process emulation

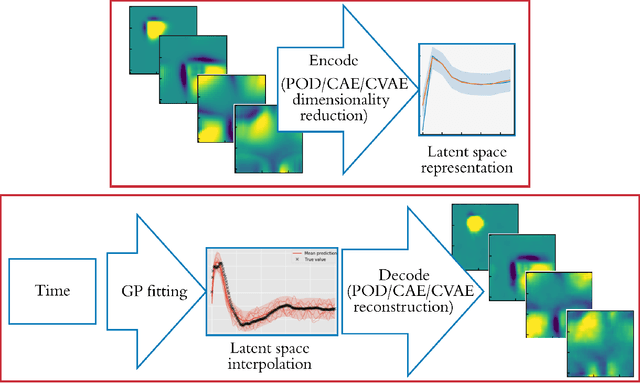
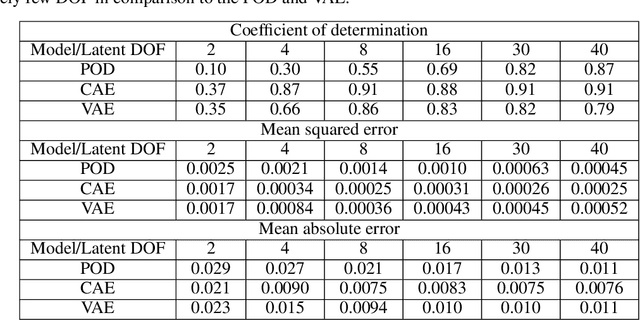
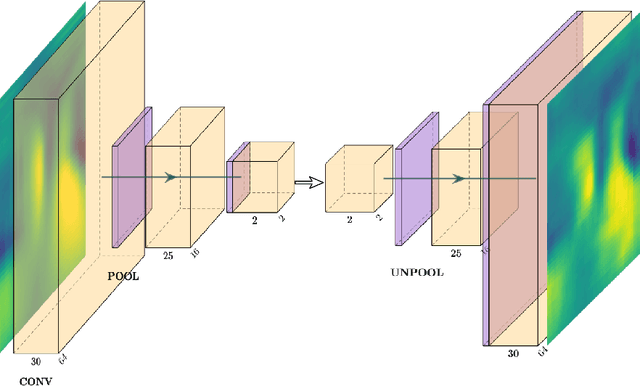
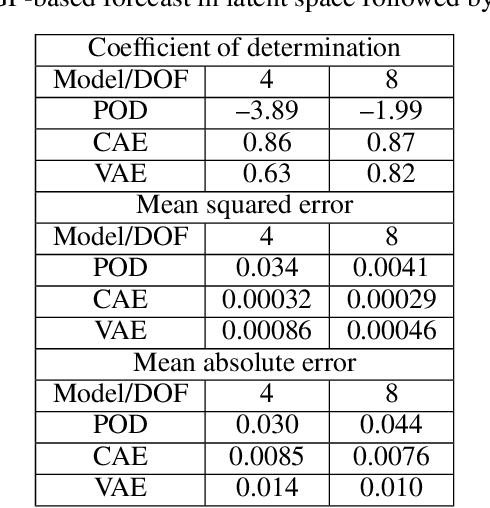
Non-intrusive reduced-order models (ROMs) have recently generated considerable interest for constructing computationally efficient counterparts of nonlinear dynamical systems emerging from various domain sciences. They provide a low-dimensional emulation framework for systems that may be intrinsically high-dimensional. This is accomplished by utilizing a construction algorithm that is purely data-driven. It is no surprise, therefore, that the algorithmic advances of machine learning have led to non-intrusive ROMs with greater accuracy and computational gains. However, in bypassing the utilization of an equation-based evolution, it is often seen that the interpretability of the ROM framework suffers. This becomes more problematic when black-box deep learning methods are used which are notorious for lacking robustness outside the physical regime of the observed data. In this article, we propose the use of a novel latent space interpolation algorithm based on Gaussian process regression. Notably, this reduced-order evolution of the system is parameterized by control parameters to allow for interpolation in space. The use of this procedure also allows for a continuous interpretation of time which allows for temporal interpolation. The latter aspect provides information, with quantified uncertainty, about full-state evolution at a finer resolution than that utilized for training the ROMs. We assess the viability of this algorithm for an advection-dominated system given by the inviscid shallow water equations.