AstroMLab 1: Who Wins Astronomy Jeopardy!?

We present a comprehensive evaluation of proprietary and open-weights large language models using the first astronomy-specific benchmarking dataset. This dataset comprises 4,425 multiple-choice questions curated from the Annual Review of Astronomy and Astrophysics, covering a broad range of astrophysical topics. Our analysis examines model performance across various astronomical subfields and assesses response calibration, crucial for potential deployment in research environments. Claude-3.5-Sonnet outperforms competitors by up to 4.6 percentage points, achieving 85.0% accuracy. For proprietary models, we observed a universal reduction in cost every 3-to-12 months to achieve similar score in this particular astronomy benchmark. Open-source models have rapidly improved, with LLaMA-3-70b (80.6%) and Qwen-2-72b (77.7%) now competing with some of the best proprietary models. We identify performance variations across topics, with non-English-focused models generally struggling more in exoplanet-related fields, stellar astrophysics, and instrumentation related questions. These challenges likely stem from less abundant training data, limited historical context, and rapid recent developments in these areas. This pattern is observed across both open-weights and proprietary models, with regional dependencies evident, highlighting the impact of training data diversity on model performance in specialized scientific domains. Top-performing models demonstrate well-calibrated confidence, with correlations above 0.9 between confidence and correctness, though they tend to be slightly underconfident. The development for fast, low-cost inference of open-weights models presents new opportunities for affordable deployment in astronomy. The rapid progress observed suggests that LLM-driven research in astronomy may become feasible in the near future.

Application of probabilistic modeling and automated machine learning framework for high-dimensional stress field

Modern computational methods, involving highly sophisticated mathematical formulations, enable several tasks like modeling complex physical phenomenon, predicting key properties and design optimization. The higher fidelity in these computer models makes it computationally intensive to query them hundreds of times for optimization and one usually relies on a simplified model albeit at the cost of losing predictive accuracy and precision. Towards this, data-driven surrogate modeling methods have shown a lot of promise in emulating the behavior of the expensive computer models. However, a major bottleneck in such methods is the inability to deal with high input dimensionality and the need for relatively large datasets. With such problems, the input and output quantity of interest are tensors of high dimensionality. Commonly used surrogate modeling methods for such problems, suffer from requirements like high number of computational evaluations that precludes one from performing other numerical tasks like uncertainty quantification and statistical analysis. In this work, we propose an end-to-end approach that maps a high-dimensional image like input to an output of high dimensionality or its key statistics. Our approach uses two main framework that perform three steps: a) reduce the input and output from a high-dimensional space to a reduced or low-dimensional space, b) model the input-output relationship in the low-dimensional space, and c) enable the incorporation of domain-specific physical constraints as masks. In order to accomplish the task of reducing input dimensionality we leverage principal component analysis, that is coupled with two surrogate modeling methods namely: a) Bayesian hybrid modeling, and b) DeepHyper's deep neural networks. We demonstrate the applicability of the approach on a problem of a linear elastic stress field data.

Interpretable Uncertainty Quantification in AI for HEP

Estimating uncertainty is at the core of performing scientific measurements in HEP: a measurement is not useful without an estimate of its uncertainty. The goal of uncertainty quantification (UQ) is inextricably linked to the question, "how do we physically and statistically interpret these uncertainties?" The answer to this question depends not only on the computational task we aim to undertake, but also on the methods we use for that task. For artificial intelligence (AI) applications in HEP, there are several areas where interpretable methods for UQ are essential, including inference, simulation, and control/decision-making. There exist some methods for each of these areas, but they have not yet been demonstrated to be as trustworthy as more traditional approaches currently employed in physics (e.g., non-AI frequentist and Bayesian methods). Shedding light on the questions above requires additional understanding of the interplay of AI systems and uncertainty quantification. We briefly discuss the existing methods in each area and relate them to tasks across HEP. We then discuss recommendations for avenues to pursue to develop the necessary techniques for reliable widespread usage of AI with UQ over the next decade.

Global field reconstruction from sparse sensors with Voronoi tessellation-assisted deep learning

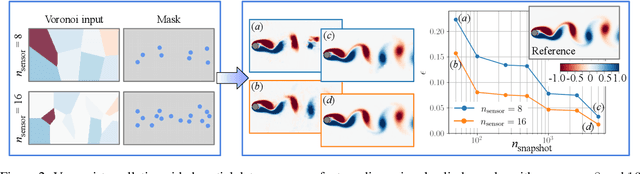
Achieving accurate and robust global situational awareness of a complex time-evolving field from a limited number of sensors has been a longstanding challenge. This reconstruction problem is especially difficult when sensors are sparsely positioned in a seemingly random or unorganized manner, which is often encountered in a range of scientific and engineering problems. Moreover, these sensors can be in motion and can become online or offline over time. The key leverage in addressing this scientific issue is the wealth of data accumulated from the sensors. As a solution to this problem, we propose a data-driven spatial field recovery technique founded on a structured grid-based deep-learning approach for arbitrary positioned sensors of any numbers. It should be noted that the na\"ive use of machine learning becomes prohibitively expensive for global field reconstruction and is furthermore not adaptable to an arbitrary number of sensors. In the present work, we consider the use of Voronoi tessellation to obtain a structured-grid representation from sensor locations enabling the computationally tractable use of convolutional neural networks. One of the central features of the present method is its compatibility with deep-learning based super-resolution reconstruction techniques for structured sensor data that are established for image processing. The proposed reconstruction technique is demonstrated for unsteady wake flow, geophysical data, and three-dimensional turbulence. The current framework is able to handle an arbitrary number of moving sensors, and thereby overcomes a major limitation with existing reconstruction methods. The presented technique opens a new pathway towards the practical use of neural networks for real-time global field estimation.

Latent-space time evolution of non-intrusive reduced-order models using Gaussian process emulation

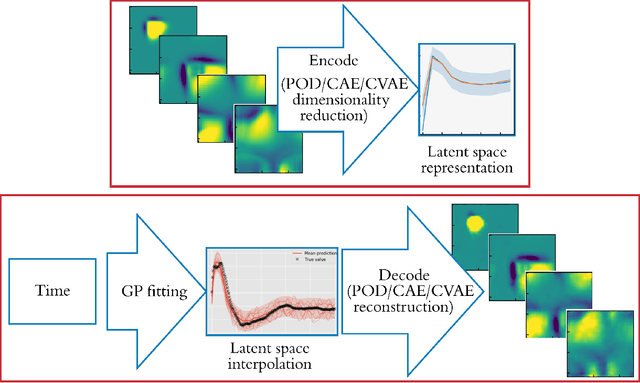
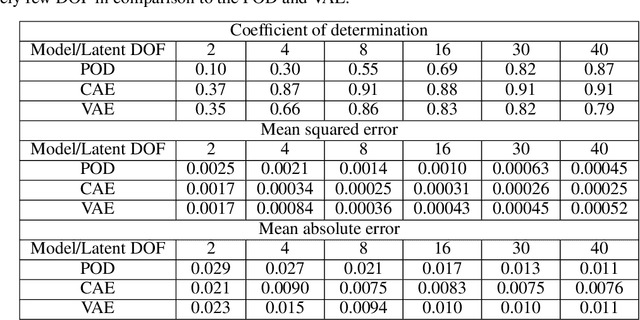
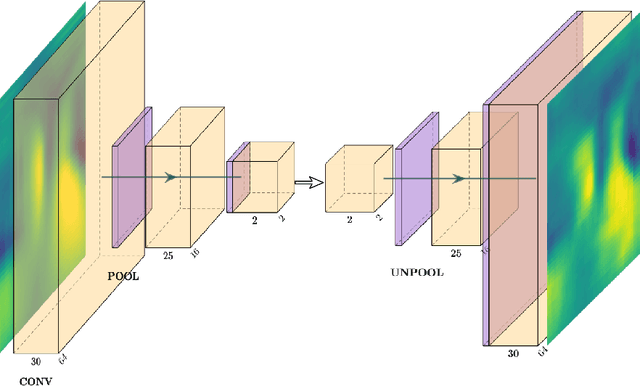
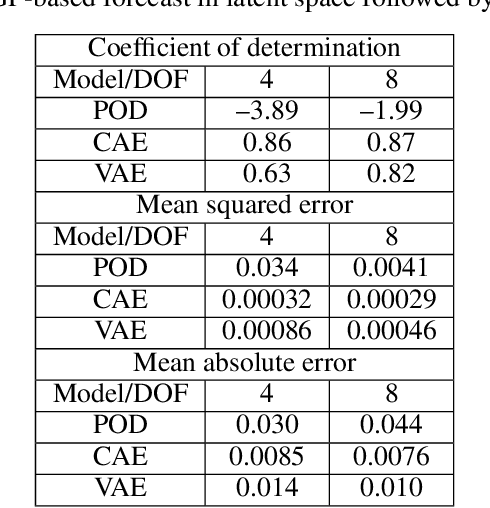
Non-intrusive reduced-order models (ROMs) have recently generated considerable interest for constructing computationally efficient counterparts of nonlinear dynamical systems emerging from various domain sciences. They provide a low-dimensional emulation framework for systems that may be intrinsically high-dimensional. This is accomplished by utilizing a construction algorithm that is purely data-driven. It is no surprise, therefore, that the algorithmic advances of machine learning have led to non-intrusive ROMs with greater accuracy and computational gains. However, in bypassing the utilization of an equation-based evolution, it is often seen that the interpretability of the ROM framework suffers. This becomes more problematic when black-box deep learning methods are used which are notorious for lacking robustness outside the physical regime of the observed data. In this article, we propose the use of a novel latent space interpolation algorithm based on Gaussian process regression. Notably, this reduced-order evolution of the system is parameterized by control parameters to allow for interpolation in space. The use of this procedure also allows for a continuous interpretation of time which allows for temporal interpolation. The latter aspect provides information, with quantified uncertainty, about full-state evolution at a finer resolution than that utilized for training the ROMs. We assess the viability of this algorithm for an advection-dominated system given by the inviscid shallow water equations.

Modular Deep Learning Analysis of Galaxy-Scale Strong Lensing Images

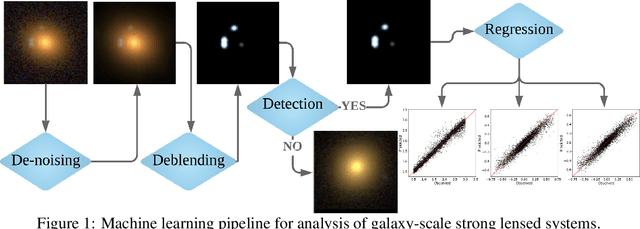
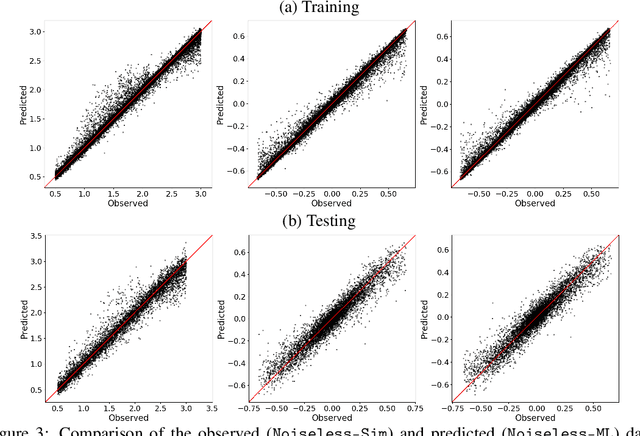
Strong gravitational lensing of astrophysical sources by foreground galaxies is a powerful cosmological tool. While such lens systems are relatively rare in the Universe, the number of detectable galaxy-scale strong lenses is expected to grow dramatically with next-generation optical surveys, numbering in the hundreds of thousands, out of tens of billions of candidate images. Automated and efficient approaches will be necessary in order to find and analyze these strong lens systems. To this end, we implement a novel, modular, end-to-end deep learning pipeline for denoising, deblending, searching, and modeling galaxy-galaxy strong lenses (GGSLs). To train and quantify the performance of our pipeline, we create a dataset of 1 million synthetic strong lensing images using state-of-the-art simulations for next-generation sky surveys. When these pretrained modules were used as a pipeline for inference, we found that the classification (searching GGSL) accuracy improved significantly---from 82% with the baseline to 90%, while the regression (modeling GGSL) accuracy improved by 25% over the baseline.