Online Covariance Matrix Estimation in Sketched Newton Methods

Given the ubiquity of streaming data, online algorithms have been widely used for parameter estimation, with second-order methods particularly standing out for their efficiency and robustness. In this paper, we study an online sketched Newton method that leverages a randomized sketching technique to perform an approximate Newton step in each iteration, thereby eliminating the computational bottleneck of second-order methods. While existing studies have established the asymptotic normality of sketched Newton methods, a consistent estimator of the limiting covariance matrix remains an open problem. We propose a fully online covariance matrix estimator that is constructed entirely from the Newton iterates and requires no matrix factorization. Compared to covariance estimators for first-order online methods, our estimator for second-order methods is batch-free. We establish the consistency and convergence rate of our estimator, and coupled with asymptotic normality results, we can then perform online statistical inference for the model parameters based on sketched Newton methods. We also discuss the extension of our estimator to constrained problems, and demonstrate its superior performance on regression problems as well as benchmark problems in the CUTEst set.

Extended Kalman filter -- Koopman operator for tractable stochastic optimal control

It has been more than seven decades since the introduction of the theory of dual control \cite{feldbaum1960dual}. Although it has provided rich insights to the fields of control, estimation, and system identification, dual control is generally computationally prohibitive. In recent years, however, the use of Koopman operator theory for control applications has been emerging. The paper presents a new reformulation of the stochastic optimal control problem that, employing the Koopman operator, yields a standard LQR problem with the dual control as its solution. We conclude the paper with a numerical example that demonstrates the effectiveness of the proposed approach, compared to certainty equivalence control, when applied to systems with varying observability.

Network Cascade Vulnerability using Constrained Bayesian Optimization

Measures of power grid vulnerability are often assessed by the amount of damage an adversary can exact on the network. However, the cascading impact of such attacks is often overlooked, even though cascades are one of the primary causes of large-scale blackouts. This paper explores modifications of transmission line protection settings as candidates for adversarial attacks, which can remain undetectable as long as the network equilibrium state remains unaltered. This forms the basis of a black-box function in a Bayesian optimization procedure, where the objective is to find protection settings that maximize network degradation due to cascading. Extensive experiments reveal that, against conventional wisdom, maximally misconfiguring the protection settings of all network lines does not cause the most cascading. More surprisingly, even when the degree of misconfiguration is resource constrained, it is still possible to find settings that produce cascades comparable in severity to instances where there are no constraints.

Application of probabilistic modeling and automated machine learning framework for high-dimensional stress field

Modern computational methods, involving highly sophisticated mathematical formulations, enable several tasks like modeling complex physical phenomenon, predicting key properties and design optimization. The higher fidelity in these computer models makes it computationally intensive to query them hundreds of times for optimization and one usually relies on a simplified model albeit at the cost of losing predictive accuracy and precision. Towards this, data-driven surrogate modeling methods have shown a lot of promise in emulating the behavior of the expensive computer models. However, a major bottleneck in such methods is the inability to deal with high input dimensionality and the need for relatively large datasets. With such problems, the input and output quantity of interest are tensors of high dimensionality. Commonly used surrogate modeling methods for such problems, suffer from requirements like high number of computational evaluations that precludes one from performing other numerical tasks like uncertainty quantification and statistical analysis. In this work, we propose an end-to-end approach that maps a high-dimensional image like input to an output of high dimensionality or its key statistics. Our approach uses two main framework that perform three steps: a) reduce the input and output from a high-dimensional space to a reduced or low-dimensional space, b) model the input-output relationship in the low-dimensional space, and c) enable the incorporation of domain-specific physical constraints as masks. In order to accomplish the task of reducing input dimensionality we leverage principal component analysis, that is coupled with two surrogate modeling methods namely: a) Bayesian hybrid modeling, and b) DeepHyper's deep neural networks. We demonstrate the applicability of the approach on a problem of a linear elastic stress field data.

Graph Neural Network-Inspired Kernels for Gaussian Processes in Semi-Supervised Learning

Gaussian processes (GPs) are an attractive class of machine learning models because of their simplicity and flexibility as building blocks of more complex Bayesian models. Meanwhile, graph neural networks (GNNs) emerged recently as a promising class of models for graph-structured data in semi-supervised learning and beyond. Their competitive performance is often attributed to a proper capturing of the graph inductive bias. In this work, we introduce this inductive bias into GPs to improve their predictive performance for graph-structured data. We show that a prominent example of GNNs, the graph convolutional network, is equivalent to some GP when its layers are infinitely wide; and we analyze the kernel universality and the limiting behavior in depth. We further present a programmable procedure to compose covariance kernels inspired by this equivalence and derive example kernels corresponding to several interesting members of the GNN family. We also propose a computationally efficient approximation of the covariance matrix for scalable posterior inference with large-scale data. We demonstrate that these graph-based kernels lead to competitive classification and regression performance, as well as advantages in computation time, compared with the respective GNNs.

Near-Optimal Distributed Linear-Quadratic Regulator for Networked Systems

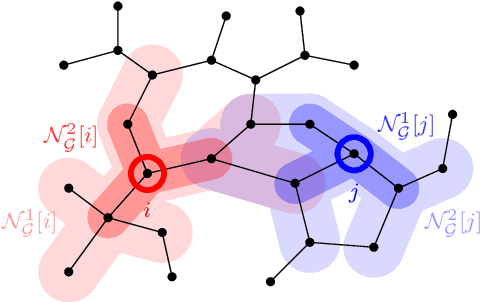
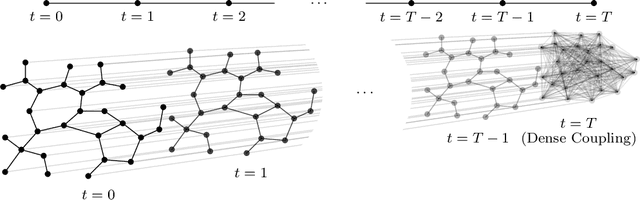
This paper studies the trade-off between the degree of decentralization and the performance of a distributed controller in a linear-quadratic control setting. We study a system of interconnected agents over a graph and a distributed controller, called $\kappa$-distributed control, which lets the agents make control decisions based on the state information within distance $\kappa$ on the underlying graph. This controller can tune its degree of decentralization using the parameter $\kappa$ and thus allows a characterization of the relationship between decentralization and performance. We show that under mild assumptions, including stabilizability, detectability, and a polynomially growing graph condition, the performance difference between $\kappa$-distributed control and centralized optimal control becomes exponentially small in $\kappa$. This result reveals that distributed control can achieve near-optimal performance with a moderate degree of decentralization, and thus it is an effective controller architecture for large-scale networked systems.

Inequality Constrained Stochastic Nonlinear Optimization via Active-Set Sequential Quadratic Programming

We study nonlinear optimization problems with stochastic objective and deterministic equality and inequality constraints, which emerge in numerous applications including finance, manufacturing, power systems and, recently, deep neural networks. We propose an active-set stochastic sequential quadratic programming algorithm, using a differentiable exact augmented Lagrangian as the merit function. The algorithm adaptively selects the penalty parameters of augmented Lagrangian and performs stochastic line search to decide the stepsize. The global convergence is established: for any initialization, the "liminf" of the KKT residuals converges to zero almost surely. Our algorithm and analysis further develop the prior work \cite{Na2021Adaptive} by allowing nonlinear inequality constraints. We demonstrate the performance of the algorithm on a subset of nonlinear problems collected in the CUTEst test set.

Randomized Algorithms for Scientific Computing (RASC)

Randomized algorithms have propelled advances in artificial intelligence and represent a foundational research area in advancing AI for Science. Future advancements in DOE Office of Science priority areas such as climate science, astrophysics, fusion, advanced materials, combustion, and quantum computing all require randomized algorithms for surmounting challenges of complexity, robustness, and scalability. This report summarizes the outcomes of that workshop, "Randomized Algorithms for Scientific Computing (RASC)," held virtually across four days in December 2020 and January 2021.

An Adaptive Stochastic Sequential Quadratic Programming with Differentiable Exact Augmented Lagrangians

We consider the problem of solving nonlinear optimization programs with stochastic objective and deterministic equality constraints. We assume for the objective that the function evaluation, the gradient, and the Hessian are inaccessible, while one can compute their stochastic estimates by, for example, subsampling. We propose a stochastic algorithm based on sequential quadratic programming (SQP) that uses a differentiable exact augmented Lagrangian as the merit function. To motivate our algorithm, we revisit an old SQP method \citep{Lucidi1990Recursive} developed for deterministic programs. We simplify that method and derive an adaptive SQP, which serves as the skeleton of our stochastic algorithm. Based on the derived algorithm, we then propose a non-adaptive SQP for optimizing stochastic objectives, where the gradient and the Hessian are replaced by stochastic estimates but the stepsize is deterministic and prespecified. Finally, we incorporate a recent stochastic line search procedure \citep{Paquette2020Stochastic} into our non-adaptive stochastic SQP to arrive at an adaptive stochastic SQP. To our knowledge, the proposed algorithm is the first stochastic SQP that allows a line search procedure and the first stochastic line search procedure that allows the constraints. The global convergence for all proposed SQP methods is established, while numerical experiments on nonlinear problems in the CUTEst test set demonstrate the superiority of the proposed algorithm.

Overlapping Schwarz Decomposition for Nonlinear Optimal Control

We present an overlapping Schwarz decomposition algorithm for solving nonlinear optimal control problems (OCPs). Our approach decomposes the time domain into a set of overlapping subdomains and solves subproblems defined over such subdomains in parallel. Convergence is attained by updating primal-dual information at the boundaries of the overlapping regions. We show that the algorithm exhibits local convergence and that the convergence rate improves exponentially with the size of the overlap. Our convergence results rely on a sensitivity result for OCPs that we call "asymptotic decay of sensitivity." Intuitively, this result states that impact of parametric perturbations at the boundaries of the time domain (initial and final time) decays exponentially as one moves away from the perturbation points. We show that this condition holds for nonlinear OCPs under a uniform second-order sufficient condition, a controllability condition, and a uniform boundedness condition. The approach is demonstrated by using a highly nonlinear quadrotor motion planning problem.