Empirical Error Estimates for Graph Sparsification

Graph sparsification is a well-established technique for accelerating graph-based learning algorithms, which uses edge sampling to approximate dense graphs with sparse ones. Because the sparsification error is random and unknown, users must contend with uncertainty about the reliability of downstream computations. Although it is possible for users to obtain conceptual guidance from theoretical error bounds in the literature, such results are typically impractical at a numerical level. Taking an alternative approach, we propose to address these issues from a data-driven perspective by computing empirical error estimates. The proposed error estimates are highly versatile, and we demonstrate this in four use cases: Laplacian matrix approximation, graph cut queries, graph-structured regression, and spectral clustering. Moreover, we provide two theoretical guarantees for the error estimates, and explain why the cost of computing them is manageable in comparison to the overall cost of a typical graph sparsification workflow.

Error Estimation for Random Fourier Features

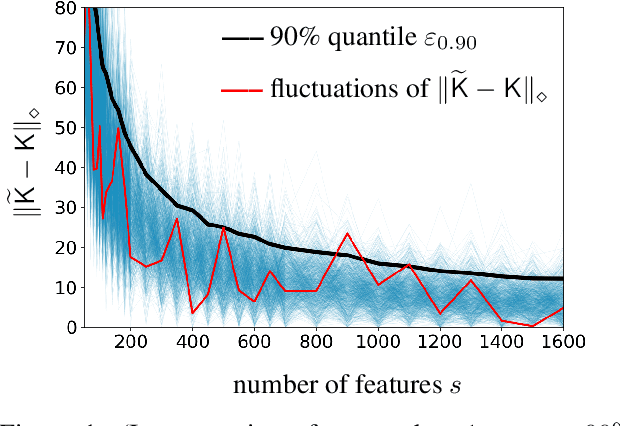
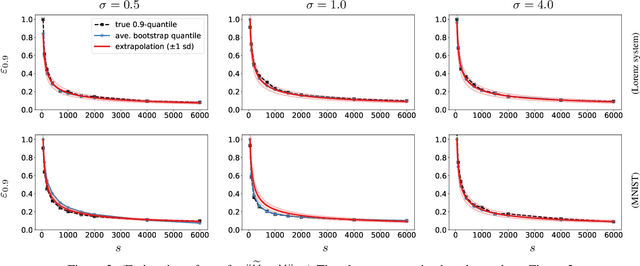
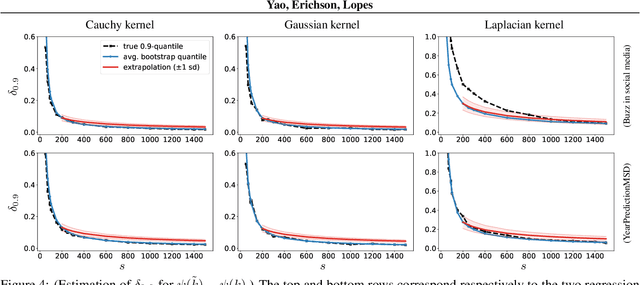
Random Fourier Features (RFF) is among the most popular and broadly applicable approaches for scaling up kernel methods. In essence, RFF allows the user to avoid costly computations on a large kernel matrix via a fast randomized approximation. However, a pervasive difficulty in applying RFF is that the user does not know the actual error of the approximation, or how this error will propagate into downstream learning tasks. Up to now, the RFF literature has primarily dealt with these uncertainties using theoretical error bounds, but from a user's standpoint, such results are typically impractical -- either because they are highly conservative or involve unknown quantities. To tackle these general issues in a data-driven way, this paper develops a bootstrap approach to numerically estimate the errors of RFF approximations. Three key advantages of this approach are: (1) The error estimates are specific to the problem at hand, avoiding the pessimism of worst-case bounds. (2) The approach is flexible with respect to different uses of RFF, and can even estimate errors in downstream learning tasks. (3) The approach enables adaptive computation, so that the user can quickly inspect the error of a rough initial kernel approximation and then predict how much extra work is needed. Lastly, in exchange for all of these benefits, the error estimates can be obtained at a modest computational cost.

Randomized Algorithms for Scientific Computing (RASC)

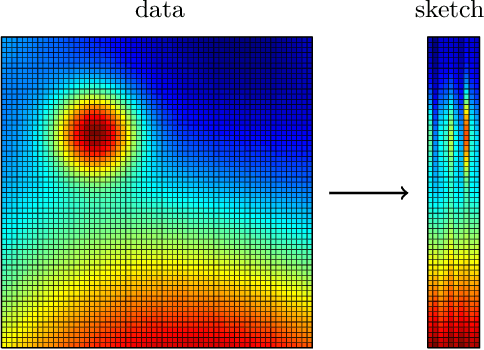
Randomized algorithms have propelled advances in artificial intelligence and represent a foundational research area in advancing AI for Science. Future advancements in DOE Office of Science priority areas such as climate science, astrophysics, fusion, advanced materials, combustion, and quantum computing all require randomized algorithms for surmounting challenges of complexity, robustness, and scalability. This report summarizes the outcomes of that workshop, "Randomized Algorithms for Scientific Computing (RASC)," held virtually across four days in December 2020 and January 2021.

Error Estimation for Sketched SVD via the Bootstrap

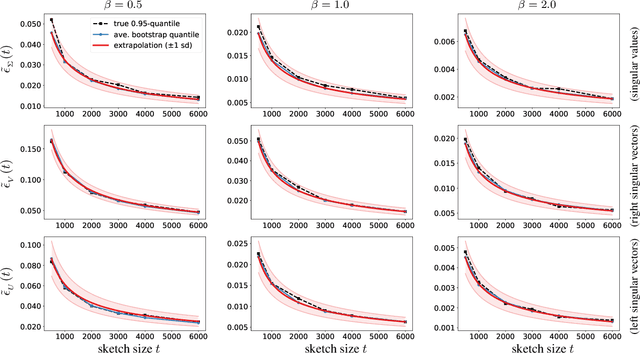
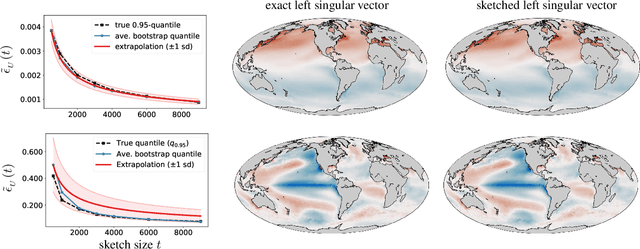
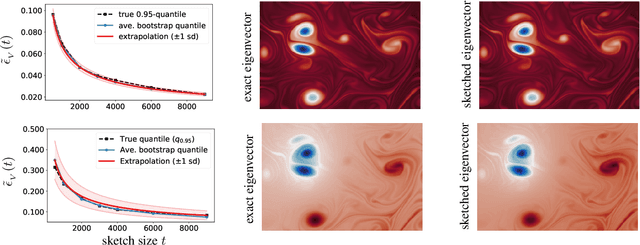
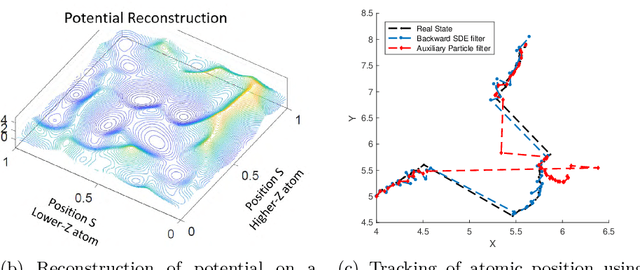
In order to compute fast approximations to the singular value decompositions (SVD) of very large matrices, randomized sketching algorithms have become a leading approach. However, a key practical difficulty of sketching an SVD is that the user does not know how far the sketched singular vectors/values are from the exact ones. Indeed, the user may be forced to rely on analytical worst-case error bounds, which do not account for the unique structure of a given problem. As a result, the lack of tools for error estimation often leads to much more computation than is really necessary. To overcome these challenges, this paper develops a fully data-driven bootstrap method that numerically estimates the actual error of sketched singular vectors/values. In particular, this allows the user to inspect the quality of a rough initial sketched SVD, and then adaptively predict how much extra work is needed to reach a given error tolerance. Furthermore, the method is computationally inexpensive, because it operates only on sketched objects, and it requires no passes over the full matrix being factored. Lastly, the method is supported by theoretical guarantees and a very encouraging set of experimental results.

Measuring the Algorithmic Convergence of Randomized Ensembles: The Regression Setting

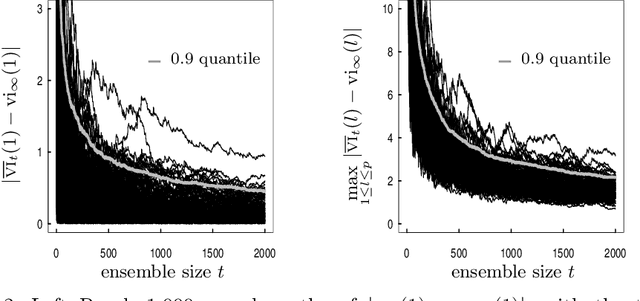
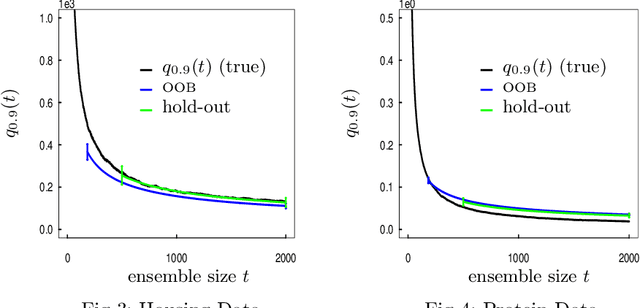
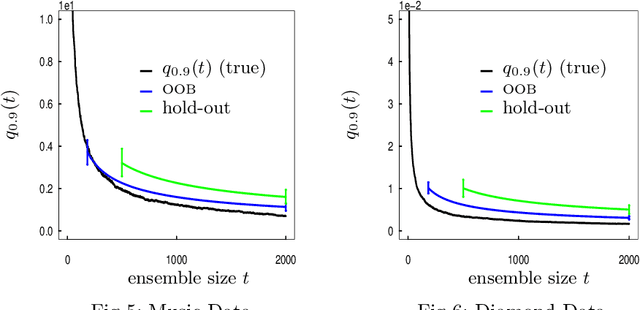
When randomized ensemble methods such as bagging and random forests are implemented, a basic question arises: Is the ensemble large enough? In particular, the practitioner desires a rigorous guarantee that a given ensemble will perform nearly as well as an ideal infinite ensemble (trained on the same data). The purpose of the current paper is to develop a bootstrap method for solving this problem in the context of regression --- which complements our companion paper in the context of classification (Lopes 2019). In contrast to the classification setting, the current paper shows that theoretical guarantees for the proposed bootstrap can be established under much weaker assumptions. In addition, we illustrate the flexibility of the method by showing how it can be adapted to measure algorithmic convergence for variable selection. Lastly, we provide numerical results demonstrating that the method works well in a range of situations.

Estimating the Algorithmic Variance of Randomized Ensembles via the Bootstrap

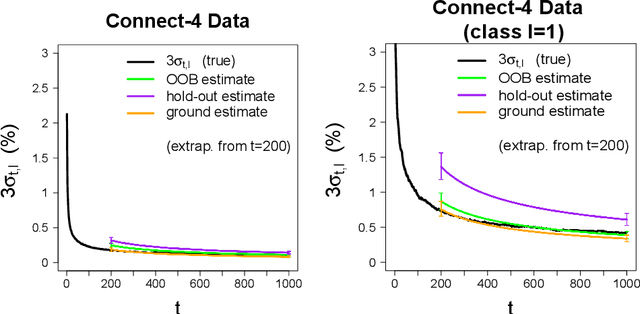
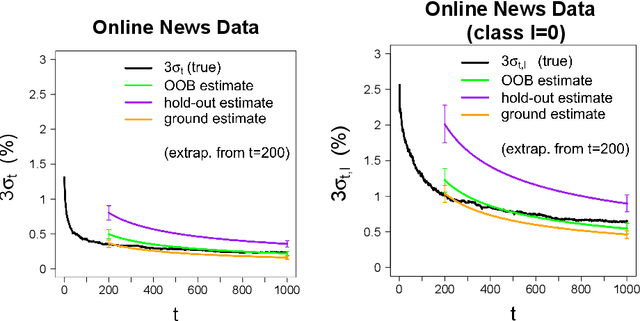
Although the methods of bagging and random forests are some of the most widely used prediction methods, relatively little is known about their algorithmic convergence. In particular, there are not many theoretical guarantees for deciding when an ensemble is "large enough" --- so that its accuracy is close to that of an ideal infinite ensemble. Due to the fact that bagging and random forests are randomized algorithms, the choice of ensemble size is closely related to the notion of "algorithmic variance" (i.e. the variance of prediction error due only to the training algorithm). In the present work, we propose a bootstrap method to estimate this variance for bagging, random forests, and related methods in the context of classification. To be specific, suppose the training dataset is fixed, and let the random variable $Err_t$ denote the prediction error of a randomized ensemble of size $t$. Working under a "first-order model" for randomized ensembles, we prove that the centered law of $Err_t$ can be consistently approximated via the proposed method as $t\to\infty$. Meanwhile, the computational cost of the method is quite modest, by virtue of an extrapolation technique. As a consequence, the method offers a practical guideline for deciding when the algorithmic fluctuations of $Err_t$ are negligible.

Error Estimation for Randomized Least-Squares Algorithms via the Bootstrap

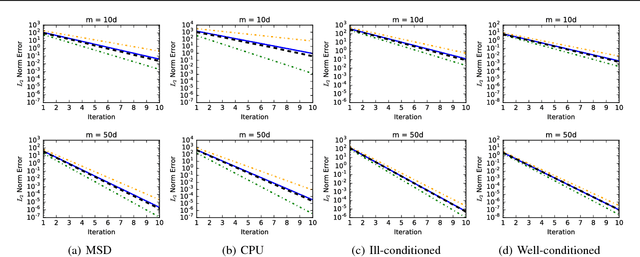
Over the course of the past decade, a variety of randomized algorithms have been proposed for computing approximate least-squares (LS) solutions in large-scale settings. A longstanding practical issue is that, for any given input, the user rarely knows the actual error of an approximate solution (relative to the exact solution). Likewise, it is difficult for the user to know precisely how much computation is needed to achieve the desired error tolerance. Consequently, the user often appeals to worst-case error bounds that tend to offer only qualitative guidance. As a more practical alternative, we propose a bootstrap method to compute a posteriori error estimates for randomized LS algorithms. These estimates permit the user to numerically assess the error of a given solution, and to predict how much work is needed to improve a "preliminary" solution. In addition, we provide theoretical consistency results for the method, which are the first such results in this context (to the best of our knowledge). From a practical standpoint, the method also has considerable flexibility, insofar as it can be applied to several popular sketching algorithms, as well as a variety of error metrics. Moreover, the extra step of error estimation does not add much cost to an underlying sketching algorithm. Finally, we demonstrate the effectiveness of the method with empirical results.

Unknown sparsity in compressed sensing: Denoising and inference

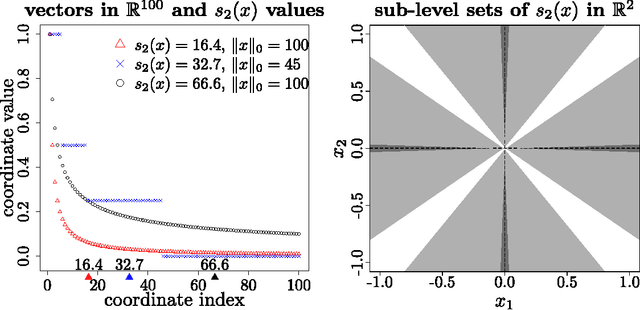
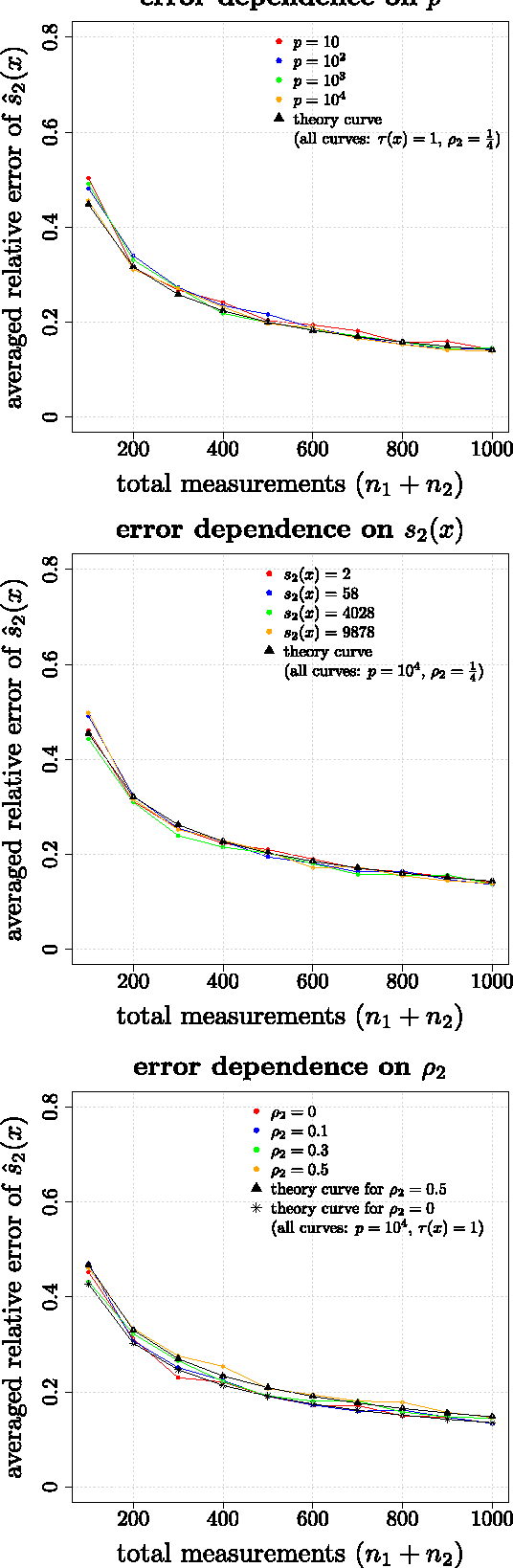
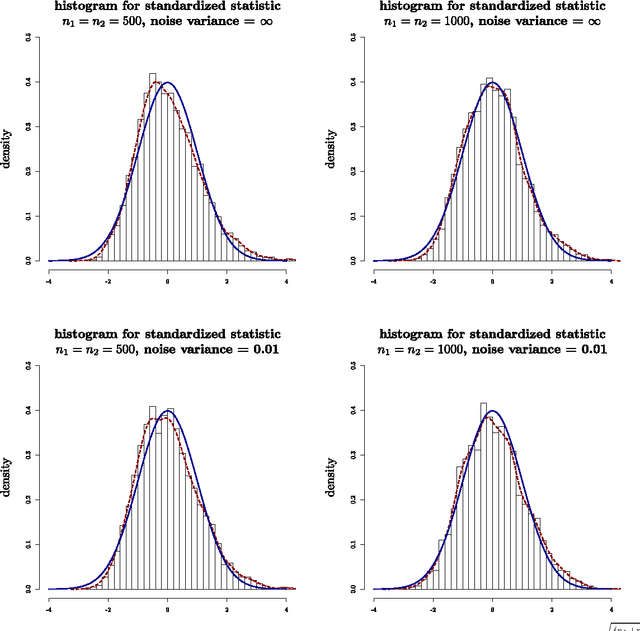
The theory of Compressed Sensing (CS) asserts that an unknown signal $x\in\mathbb{R}^p$ can be accurately recovered from an underdetermined set of $n$ linear measurements with $n\ll p$, provided that $x$ is sufficiently sparse. However, in applications, the degree of sparsity $\|x\|_0$ is typically unknown, and the problem of directly estimating $\|x\|_0$ has been a longstanding gap between theory and practice. A closely related issue is that $\|x\|_0$ is a highly idealized measure of sparsity, and for real signals with entries not equal to 0, the value $\|x\|_0=p$ is not a useful description of compressibility. In our previous conference paper [Lop13] that examined these problems, we considered an alternative measure of "soft" sparsity, $\|x\|_1^2/\|x\|_2^2$, and designed a procedure to estimate $\|x\|_1^2/\|x\|_2^2$ that does not rely on sparsity assumptions. The present work offers a new deconvolution-based method for estimating unknown sparsity, which has wider applicability and sharper theoretical guarantees. In particular, we introduce a family of entropy-based sparsity measures $s_q(x):=\big(\frac{\|x\|_q}{\|x\|_1}\big)^{\frac{q}{1-q}}$ parameterized by $q\in[0,\infty]$. This family interpolates between $\|x\|_0=s_0(x)$ and $\|x\|_1^2/\|x\|_2^2=s_2(x)$ as $q$ ranges over $[0,2]$. For any $q\in (0,2]\setminus\{1\}$, we propose an estimator $\hat{s}_q(x)$ whose relative error converges at the dimension-free rate of $1/\sqrt{n}$, even when $p/n\to\infty$. Our main results also describe the limiting distribution of $\hat{s}_q(x)$, as well as some connections to Basis Pursuit Denosing, the Lasso, deterministic measurement matrices, and inference problems in CS.

A Bootstrap Method for Error Estimation in Randomized Matrix Multiplication

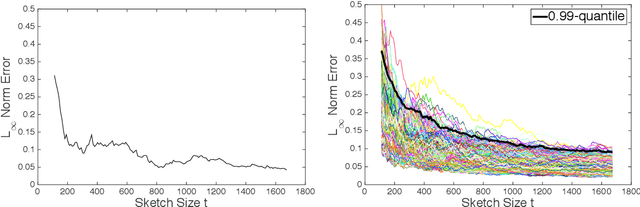
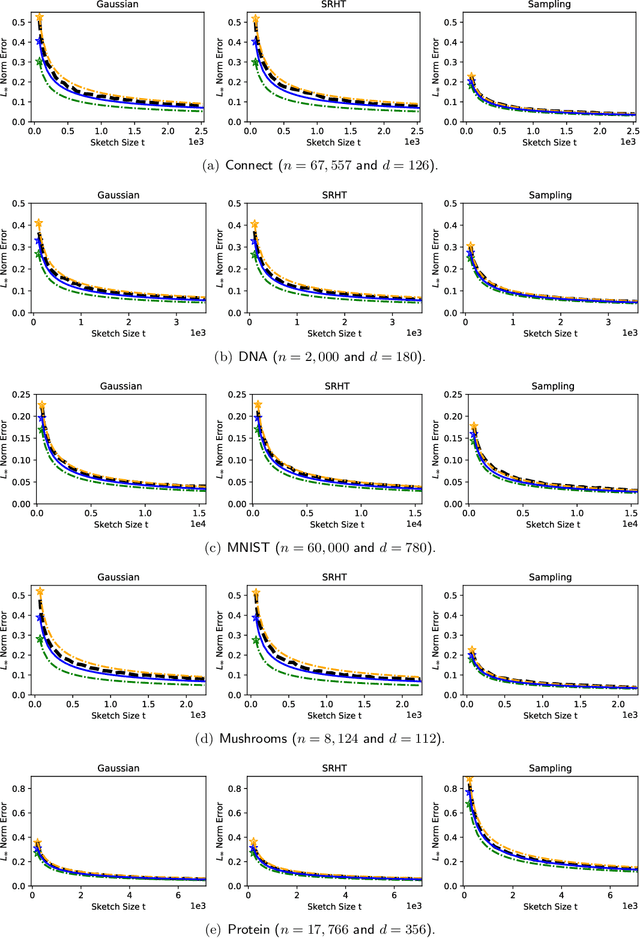
In recent years, randomized methods for numerical linear algebra have received growing interest as a general approach to large-scale problems. Typically, the essential ingredient of these methods is some form of randomized dimension reduction, which accelerates computations, but also creates random approximation error. In this way, the dimension reduction step encodes a tradeoff between cost and accuracy. However, the exact numerical relationship between cost and accuracy is typically unknown, and consequently, it may be difficult for the user to precisely know (1) how accurate a given solution is, or (2) how much computation is needed to achieve a given level of accuracy. In the current paper, we study randomized matrix multiplication (sketching) as a prototype setting for addressing these general problems. As a solution, we develop a bootstrap method for {directly estimating} the accuracy as a function of the reduced dimension (as opposed to deriving worst-case bounds on the accuracy in terms of the reduced dimension). From a computational standpoint, the proposed method does not substantially increase the cost of standard sketching methods, and this is made possible by an "extrapolation" technique. In addition, we provide both theoretical and empirical results to demonstrate the effectiveness of the proposed method.

A Residual Bootstrap for High-Dimensional Regression with Near Low-Rank Designs

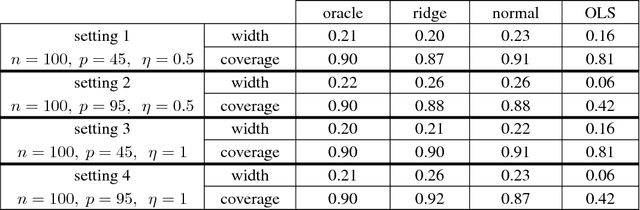
We study the residual bootstrap (RB) method in the context of high-dimensional linear regression. Specifically, we analyze the distributional approximation of linear contrasts $c^{\top} (\hat{\beta}_{\rho}-\beta)$, where $\hat{\beta}_{\rho}$ is a ridge-regression estimator. When regression coefficients are estimated via least squares, classical results show that RB consistently approximates the laws of contrasts, provided that $p\ll n$, where the design matrix is of size $n\times p$. Up to now, relatively little work has considered how additional structure in the linear model may extend the validity of RB to the setting where $p/n\asymp 1$. In this setting, we propose a version of RB that resamples residuals obtained from ridge regression. Our main structural assumption on the design matrix is that it is nearly low rank --- in the sense that its singular values decay according to a power-law profile. Under a few extra technical assumptions, we derive a simple criterion for ensuring that RB consistently approximates the law of a given contrast. We then specialize this result to study confidence intervals for mean response values $X_i^{\top} \beta$, where $X_i^{\top}$ is the $i$th row of the design. More precisely, we show that conditionally on a Gaussian design with near low-rank structure, RB simultaneously approximates all of the laws $X_i^{\top}(\hat{\beta}_{\rho}-\beta)$, $i=1,\dots,n$. This result is also notable as it imposes no sparsity assumptions on $\beta$. Furthermore, since our consistency results are formulated in terms of the Mallows (Kantorovich) metric, the existence of a limiting distribution is not required.