Improving Lung Cancer Diagnosis and Survival Prediction with Deep Learning and CT Imaging

Lung cancer is a major cause of cancer-related deaths, and early diagnosis and treatment are crucial for improving patients' survival outcomes. In this paper, we propose to employ convolutional neural networks to model the non-linear relationship between the risk of lung cancer and the lungs' morphology revealed in the CT images. We apply a mini-batched loss that extends the Cox proportional hazards model to handle the non-convexity induced by neural networks, which also enables the training of large data sets. Additionally, we propose to combine mini-batched loss and binary cross-entropy to predict both lung cancer occurrence and the risk of mortality. Simulation results demonstrate the effectiveness of both the mini-batched loss with and without the censoring mechanism, as well as its combination with binary cross-entropy. We evaluate our approach on the National Lung Screening Trial data set with several 3D convolutional neural network architectures, achieving high AUC and C-index scores for lung cancer classification and survival prediction. These results, obtained from simulations and real data experiments, highlight the potential of our approach to improving the diagnosis and treatment of lung cancer.

Low-rank Matrix Bandits with Heavy-tailed Rewards

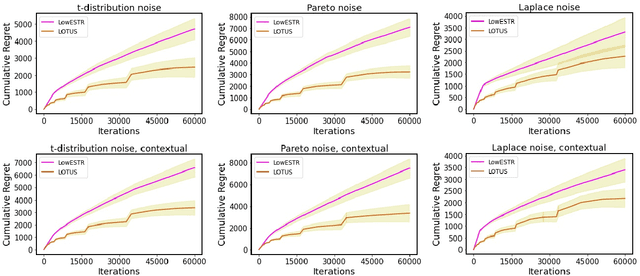
In stochastic low-rank matrix bandit, the expected reward of an arm is equal to the inner product between its feature matrix and some unknown $d_1$ by $d_2$ low-rank parameter matrix $\Theta^*$ with rank $r \ll d_1\wedge d_2$. While all prior studies assume the payoffs are mixed with sub-Gaussian noises, in this work we loosen this strict assumption and consider the new problem of \underline{low}-rank matrix bandit with \underline{h}eavy-\underline{t}ailed \underline{r}ewards (LowHTR), where the rewards only have finite $(1+\delta)$ moment for some $\delta \in (0,1]$. By utilizing the truncation on observed payoffs and the dynamic exploration, we propose a novel algorithm called LOTUS attaining the regret bound of order $\tilde O(d^\frac{3}{2}r^\frac{1}{2}T^\frac{1}{1+\delta}/\tilde{D}_{rr})$ without knowing $T$, which matches the state-of-the-art regret bound under sub-Gaussian noises~\citep{lu2021low,kang2022efficient} with $\delta = 1$. Moreover, we establish a lower bound of the order $\Omega(d^\frac{\delta}{1+\delta} r^\frac{\delta}{1+\delta} T^\frac{1}{1+\delta}) = \Omega(T^\frac{1}{1+\delta})$ for LowHTR, which indicates our LOTUS is nearly optimal in the order of $T$. In addition, we improve LOTUS so that it does not require knowledge of the rank $r$ with $\tilde O(dr^\frac{3}{2}T^\frac{1+\delta}{1+2\delta})$ regret bound, and it is efficient under the high-dimensional scenario. We also conduct simulations to demonstrate the practical superiority of our algorithm.

Efficient Frameworks for Generalized Low-Rank Matrix Bandit Problems

In the stochastic contextual low-rank matrix bandit problem, the expected reward of an action is given by the inner product between the action's feature matrix and some fixed, but initially unknown $d_1$ by $d_2$ matrix $\Theta^*$ with rank $r \ll \{d_1, d_2\}$, and an agent sequentially takes actions based on past experience to maximize the cumulative reward. In this paper, we study the generalized low-rank matrix bandit problem, which has been recently proposed in \cite{lu2021low} under the Generalized Linear Model (GLM) framework. To overcome the computational infeasibility and theoretical restrain of existing algorithms on this problem, we first propose the G-ESTT framework that modifies the idea from \cite{jun2019bilinear} by using Stein's method on the subspace estimation and then leverage the estimated subspaces via a regularization idea. Furthermore, we remarkably improve the efficiency of G-ESTT by using a novel exclusion idea on the estimated subspace instead, and propose the G-ESTS framework. We also show that G-ESTT can achieve the $\tilde{O}(\sqrt{(d_1+d_2)MrT})$ bound of regret while G-ESTS can achineve the $\tilde{O}(\sqrt{(d_1+d_2)^{3/2}Mr^{3/2}T})$ bound of regret under mild assumption up to logarithm terms, where $M$ is some problem dependent value. Under a reasonable assumption that $M = O((d_1+d_2)^2)$ in our problem setting, the regret of G-ESTT is consistent with the current best regret of $\tilde{O}((d_1+d_2)^{3/2} \sqrt{rT}/D_{rr})$~\citep{lu2021low} ($D_{rr}$ will be defined later). For completeness, we conduct experiments to illustrate that our proposed algorithms, especially G-ESTS, are also computationally tractable and consistently outperform other state-of-the-art (generalized) linear matrix bandit methods based on a suite of simulations.

Robust Lipschitz Bandits to Adversarial Corruptions

Lipschitz bandit is a variant of stochastic bandits that deals with a continuous arm set defined on a metric space, where the reward function is subject to a Lipschitz constraint. In this paper, we introduce a new problem of Lipschitz bandits in the presence of adversarial corruptions where an adaptive adversary corrupts the stochastic rewards up to a total budget $C$. The budget is measured by the sum of corruption levels across the time horizon $T$. We consider both weak and strong adversaries, where the weak adversary is unaware of the current action before the attack, while the strong one can observe it. Our work presents the first line of robust Lipschitz bandit algorithms that can achieve sub-linear regret under both types of adversary, even when the total budget of corruption $C$ is unrevealed to the agent. We provide a lower bound under each type of adversary, and show that our algorithm is optimal under the strong case. Finally, we conduct experiments to illustrate the effectiveness of our algorithms against two classic kinds of attacks.

Online Continuous Hyperparameter Optimization for Contextual Bandits

In stochastic contextual bandit problems, an agent sequentially makes actions from a time-dependent action set based on past experience to minimize the cumulative regret. Like many other machine learning algorithms, the performance of bandits heavily depends on their multiple hyperparameters, and theoretically derived parameter values may lead to unsatisfactory results in practice. Moreover, it is infeasible to use offline tuning methods like cross validation to choose hyperparameters under the bandit environment, as the decisions should be made in real time. To address this challenge, we propose the first online continuous hyperparameter tuning framework for contextual bandits to learn the optimal parameter configuration within a search space on the fly. Specifically, we use a double-layer bandit framework named CDT (Continuous Dynamic Tuning) and formulate the hyperparameter optimization as a non-stationary continuum-armed bandit, where each arm represents a combination of hyperparameters, and the corresponding reward is the algorithmic result. For the top layer, we propose the Zooming TS algorithm that utilizes Thompson Sampling (TS) for exploration and a restart technique to get around the switching environment. The proposed CDT framework can be easily used to tune contextual bandit algorithms without any pre-specified candidate set for hyperparameters. We further show that it could achieve sublinear regret in theory and performs consistently better on both synthetic and real datasets in practice.

Extending the Use of MDL for High-Dimensional Problems: Variable Selection, Robust Fitting, and Additive Modeling

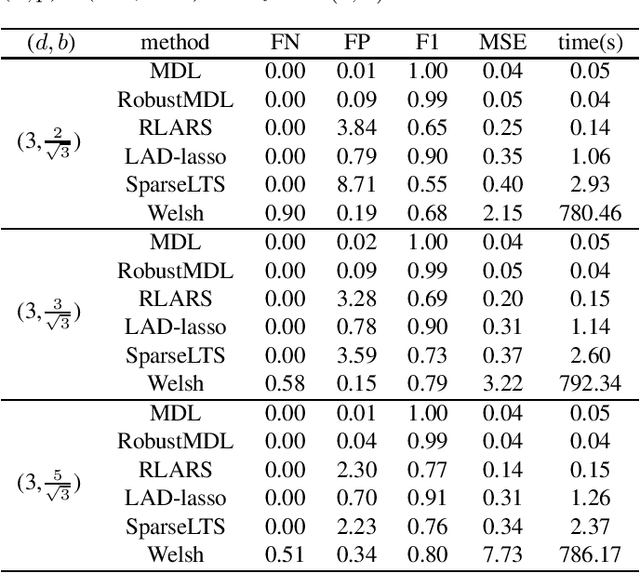
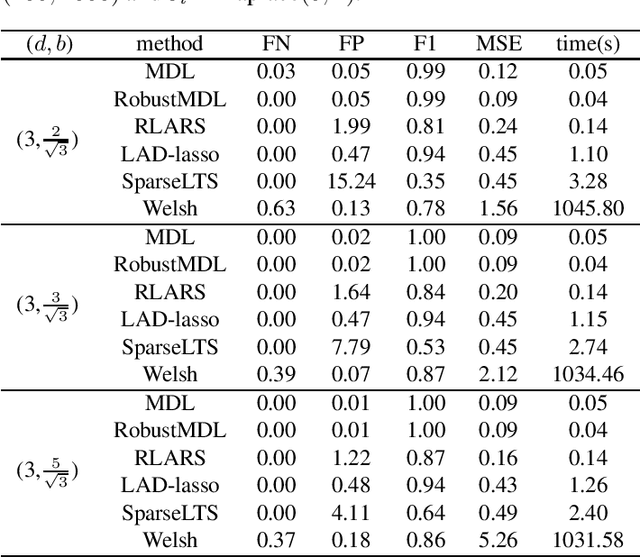
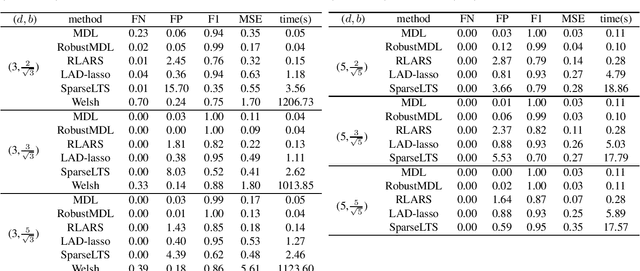
In the signal processing and statistics literature, the minimum description length (MDL) principle is a popular tool for choosing model complexity. Successful examples include signal denoising and variable selection in linear regression, for which the corresponding MDL solutions often enjoy consistent properties and produce very promising empirical results. This paper demonstrates that MDL can be extended naturally to the high-dimensional setting, where the number of predictors $p$ is larger than the number of observations $n$. It first considers the case of linear regression, then allows for outliers in the data, and lastly extends to the robust fitting of nonparametric additive models. Results from numerical experiments are presented to demonstrate the efficiency and effectiveness of the MDL approach.

A Review of Adversarial Attack and Defense for Classification Methods

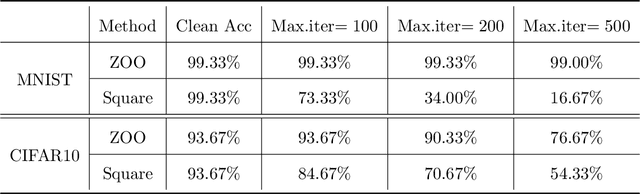
Despite the efficiency and scalability of machine learning systems, recent studies have demonstrated that many classification methods, especially deep neural networks (DNNs), are vulnerable to adversarial examples; i.e., examples that are carefully crafted to fool a well-trained classification model while being indistinguishable from natural data to human. This makes it potentially unsafe to apply DNNs or related methods in security-critical areas. Since this issue was first identified by Biggio et al. (2013) and Szegedy et al.(2014), much work has been done in this field, including the development of attack methods to generate adversarial examples and the construction of defense techniques to guard against such examples. This paper aims to introduce this topic and its latest developments to the statistical community, primarily focusing on the generation and guarding of adversarial examples. Computing codes (in python and R) used in the numerical experiments are publicly available for readers to explore the surveyed methods. It is the hope of the authors that this paper will encourage more statisticians to work on this important and exciting field of generating and defending against adversarial examples.

Detecting Adversarial Examples with Bayesian Neural Network

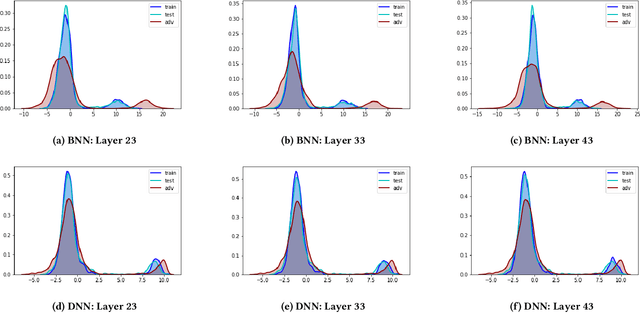
In this paper, we propose a new framework to detect adversarial examples motivated by the observations that random components can improve the smoothness of predictors and make it easier to simulate output distribution of deep neural network. With these observations, we propose a novel Bayesian adversarial example detector, short for BATer, to improve the performance of adversarial example detection. In specific, we study the distributional difference of hidden layer output between natural and adversarial examples, and propose to use the randomness of Bayesian neural network (BNN) to simulate hidden layer output distribution and leverage the distribution dispersion to detect adversarial examples. The advantage of BNN is that the output is stochastic while neural networks without random components do not have such characteristics. Empirical results on several benchmark datasets against popular attacks show that the proposed BATer outperforms the state-of-the-art detectors in adversarial example detection.

Uncertainty Quantification in Ensembles of Honest Regression Trees using Generalized Fiducial Inference

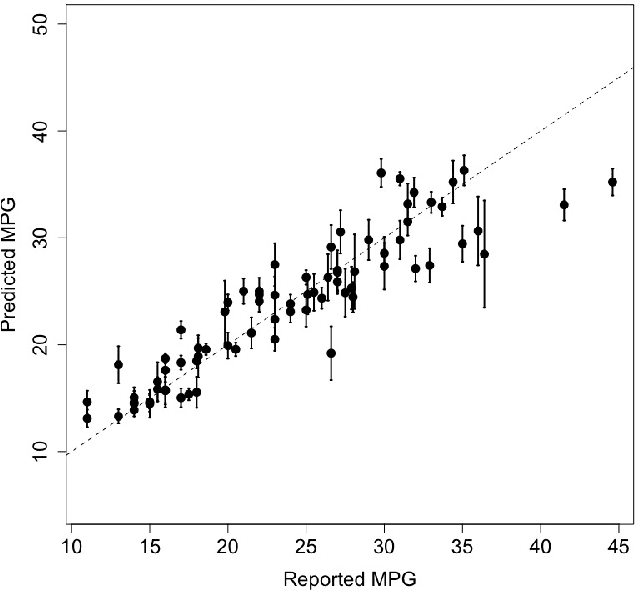
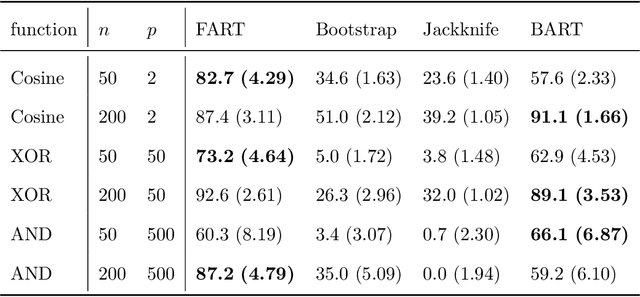
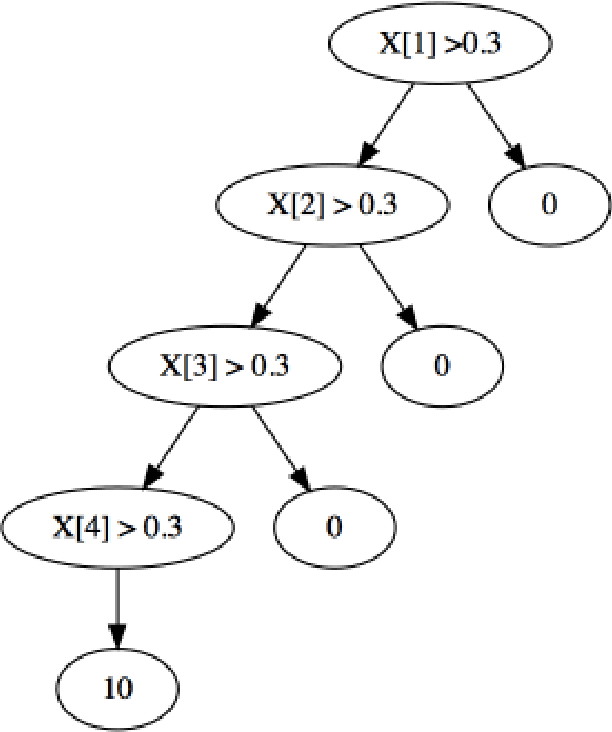
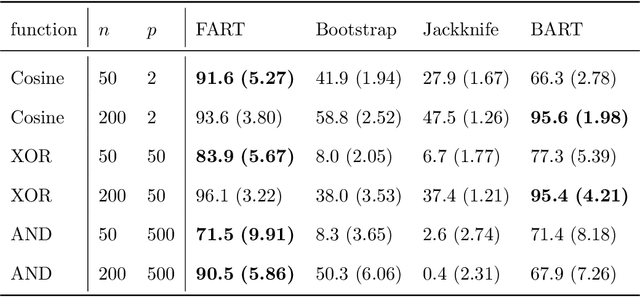
Due to their accuracies, methods based on ensembles of regression trees are a popular approach for making predictions. Some common examples include Bayesian additive regression trees, boosting and random forests. This paper focuses on honest random forests, which add honesty to the original form of random forests and are proved to have better statistical properties. The main contribution is a new method that quantifies the uncertainties of the estimates and predictions produced by honest random forests. The proposed method is based on the generalized fiducial methodology, and provides a fiducial density function that measures how likely each single honest tree is the true model. With such a density function, estimates and predictions, as well as their confidence/prediction intervals, can be obtained. The promising empirical properties of the proposed method are demonstrated by numerical comparisons with several state-of-the-art methods, and by applications to a few real data sets. Lastly, the proposed method is theoretically backed up by a strong asymptotic guarantee.

Measuring the Algorithmic Convergence of Randomized Ensembles: The Regression Setting

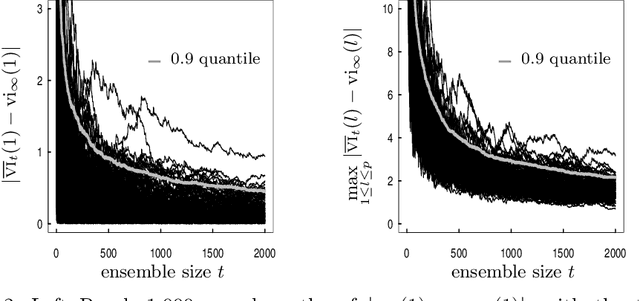
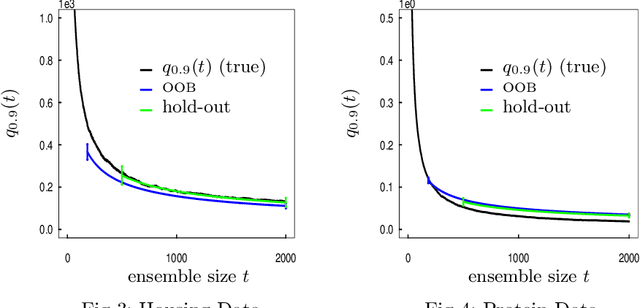
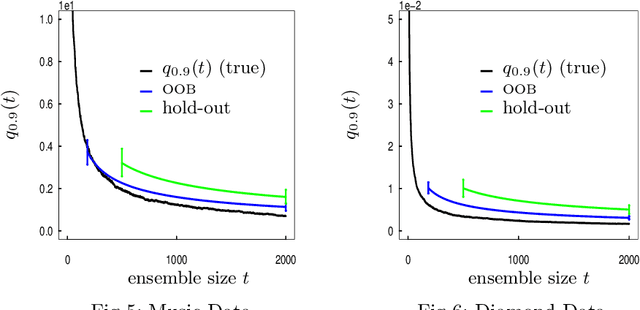
When randomized ensemble methods such as bagging and random forests are implemented, a basic question arises: Is the ensemble large enough? In particular, the practitioner desires a rigorous guarantee that a given ensemble will perform nearly as well as an ideal infinite ensemble (trained on the same data). The purpose of the current paper is to develop a bootstrap method for solving this problem in the context of regression --- which complements our companion paper in the context of classification (Lopes 2019). In contrast to the classification setting, the current paper shows that theoretical guarantees for the proposed bootstrap can be established under much weaker assumptions. In addition, we illustrate the flexibility of the method by showing how it can be adapted to measure algorithmic convergence for variable selection. Lastly, we provide numerical results demonstrating that the method works well in a range of situations.