Extending the Use of MDL for High-Dimensional Problems: Variable Selection, Robust Fitting, and Additive Modeling

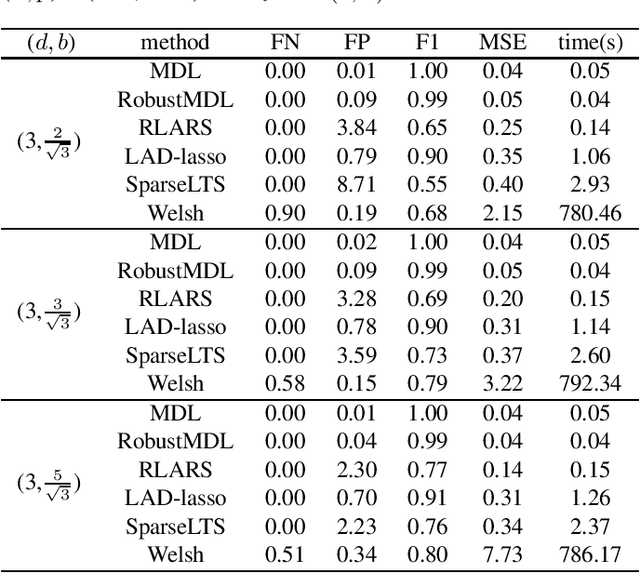
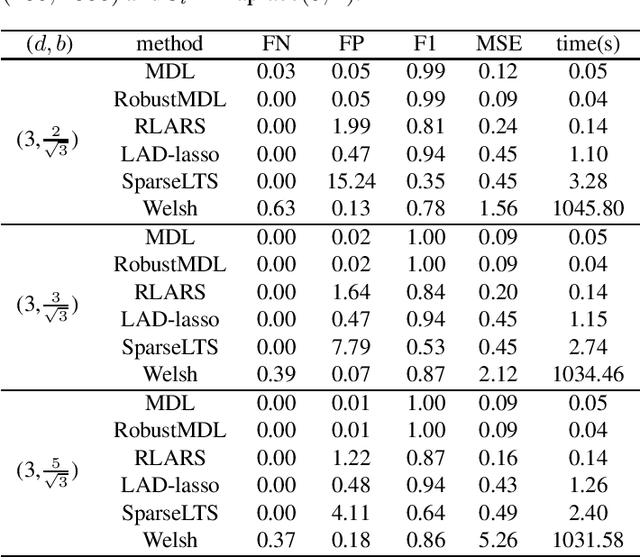
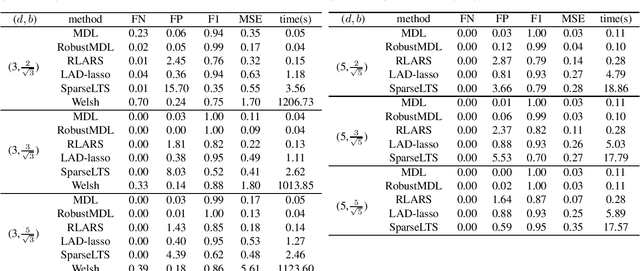
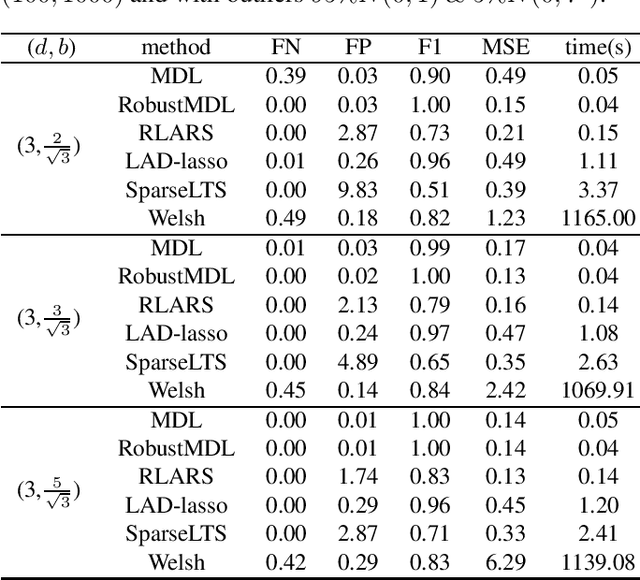
In the signal processing and statistics literature, the minimum description length (MDL) principle is a popular tool for choosing model complexity. Successful examples include signal denoising and variable selection in linear regression, for which the corresponding MDL solutions often enjoy consistent properties and produce very promising empirical results. This paper demonstrates that MDL can be extended naturally to the high-dimensional setting, where the number of predictors $p$ is larger than the number of observations $n$. It first considers the case of linear regression, then allows for outliers in the data, and lastly extends to the robust fitting of nonparametric additive models. Results from numerical experiments are presented to demonstrate the efficiency and effectiveness of the MDL approach.