Visual High Dimensional Hypothesis Testing

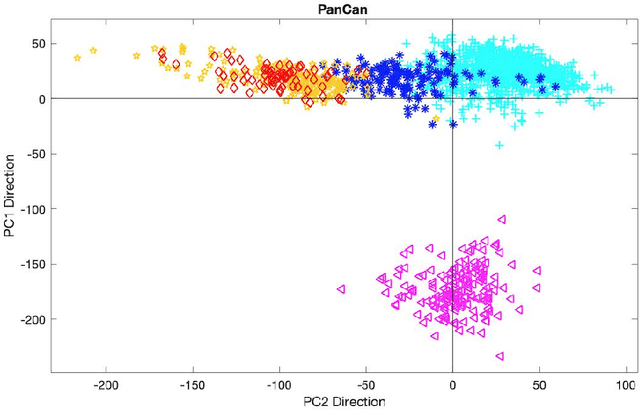
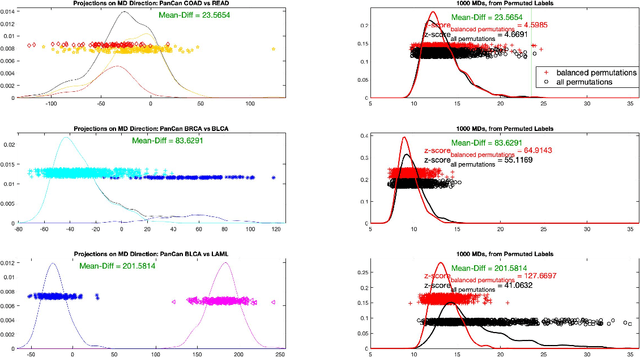
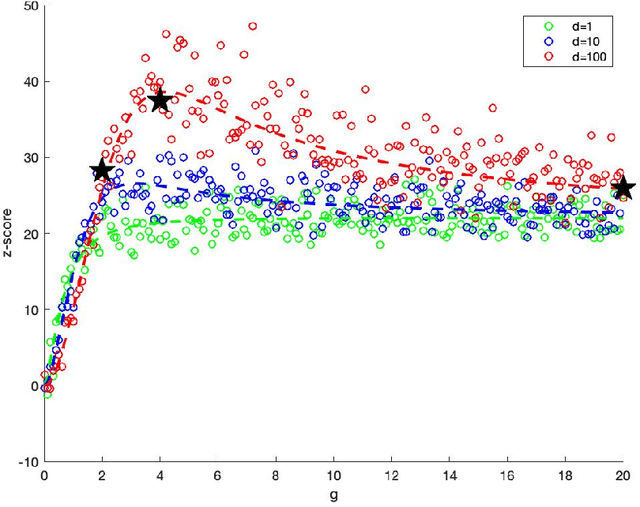
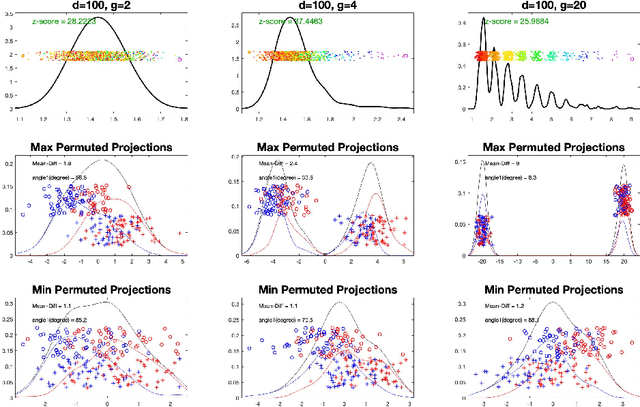
In exploratory data analysis of known classes of high dimensional data, a central question is how distinct are the classes? The Direction Projection Permutation (DiProPerm) hypothesis test provides an answer to this that is directly connected to a visual analysis of the data. In this paper, we propose an improved DiProPerm test that solves 3 major challenges of the original version. First, we implement only balanced permutations to increase the test power for data with strong signals. Second, our mathematical analysis leads to an adjustment to correct the null behavior of both balanced and the conventional all permutations. Third, new confidence intervals (reflecting permutation variation) for test significance are also proposed for comparison of results across different contexts. This improvement of DiProPerm inference is illustrated in the context of comparing cancer types in examples from The Cancer Genome Atlas.

Deep Fiducial Inference

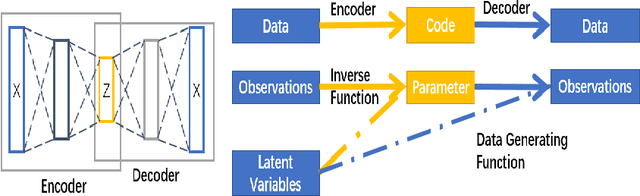
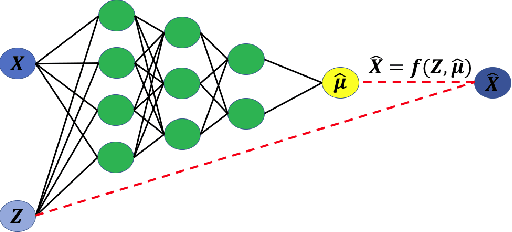
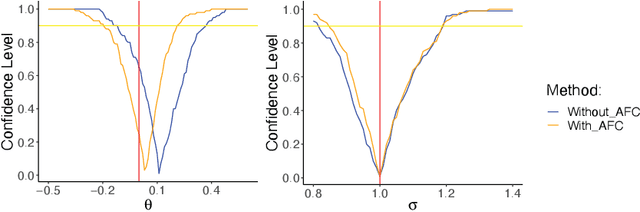
Since the mid-2000s, there has been a resurrection of interest in modern modifications of fiducial inference. To date, the main computational tool to extract a generalized fiducial distribution is Markov chain Monte Carlo (MCMC). We propose an alternative way of computing a generalized fiducial distribution that could be used in complex situations. In particular, to overcome the difficulty when the unnormalized fiducial density (needed for MCMC), we design a fiducial autoencoder (FAE). The fitted autoencoder is used to generate generalized fiducial samples of the unknown parameters. To increase accuracy, we then apply an approximate fiducial computation (AFC) algorithm, by rejecting samples that when plugged into a decoder do not replicate the observed data well enough. Our numerical experiments show the effectiveness of our FAE-based inverse solution and the excellent coverage performance of the AFC corrected FAE solution.

Uncertainty Quantification in Ensembles of Honest Regression Trees using Generalized Fiducial Inference

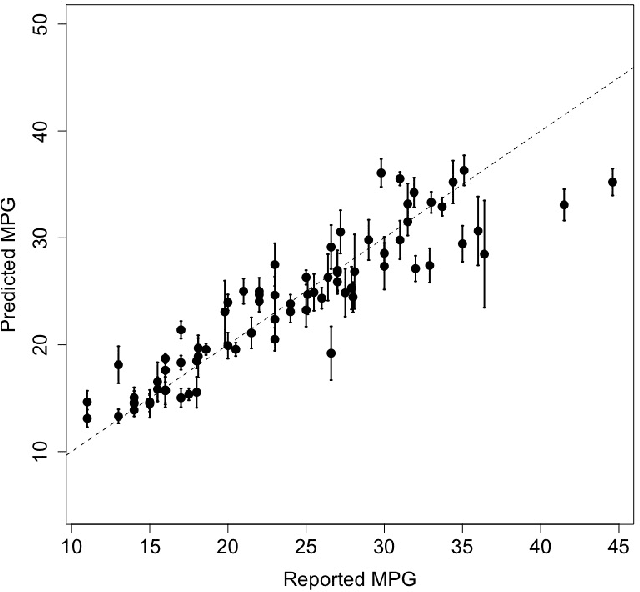
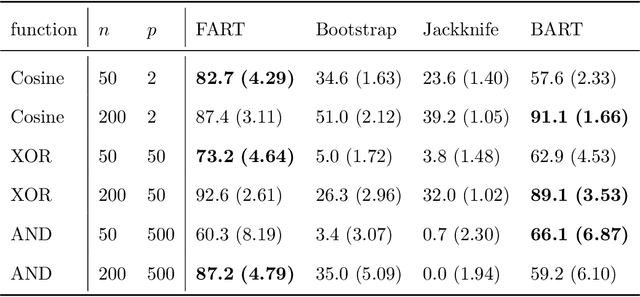
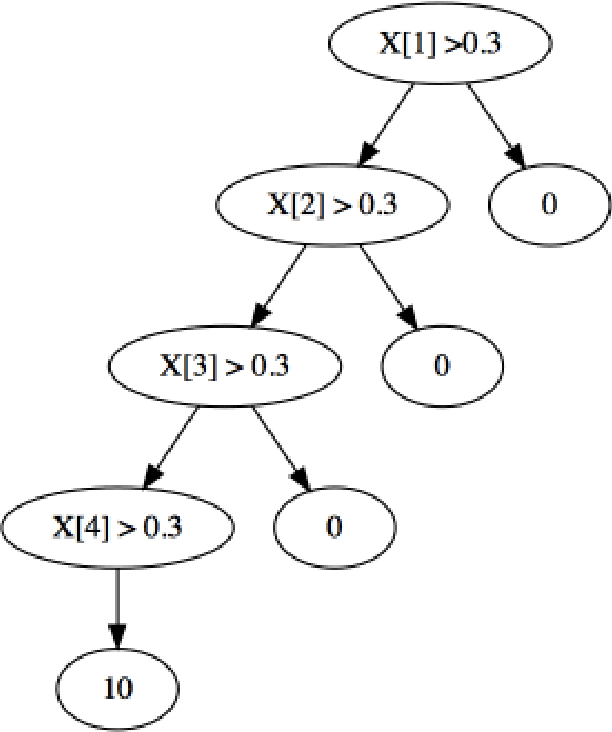
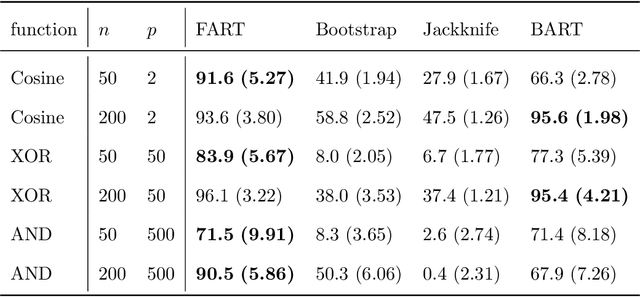
Due to their accuracies, methods based on ensembles of regression trees are a popular approach for making predictions. Some common examples include Bayesian additive regression trees, boosting and random forests. This paper focuses on honest random forests, which add honesty to the original form of random forests and are proved to have better statistical properties. The main contribution is a new method that quantifies the uncertainties of the estimates and predictions produced by honest random forests. The proposed method is based on the generalized fiducial methodology, and provides a fiducial density function that measures how likely each single honest tree is the true model. With such a density function, estimates and predictions, as well as their confidence/prediction intervals, can be obtained. The promising empirical properties of the proposed method are demonstrated by numerical comparisons with several state-of-the-art methods, and by applications to a few real data sets. Lastly, the proposed method is theoretically backed up by a strong asymptotic guarantee.

A Note on Optimal Sampling Strategy for Structural Variant Detection Using Optical Mapping

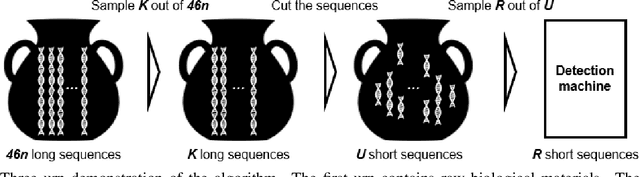
Structural variants compose the majority of human genetic variation, but are difficult to assess using current genomic sequencing technologies. Optical mapping technologies, which measure the size of chromosomal fragments between labeled markers, offer an alternative approach. As these technologies mature towards becoming clinical tools, there is a need to develop an approach for determining the optimal strategy for sampling biological material in order to detect a variant at some threshold. Here we develop an optimization approach using a simple, yet realistic, model of the genomic mapping process using a hyper-geometric distribution and {probabilistic} concentration inequalities. Our approach is both computationally and analytically tractable and includes a novel approach to getting tail bounds of hyper-geometric distribution. We show that if a genomic mapping technology can sample most of the chromosomal fragments within a sample, comparatively little biological material is needed to detect a variant at high confidence.

Subspace Clustering through Sub-Clusters

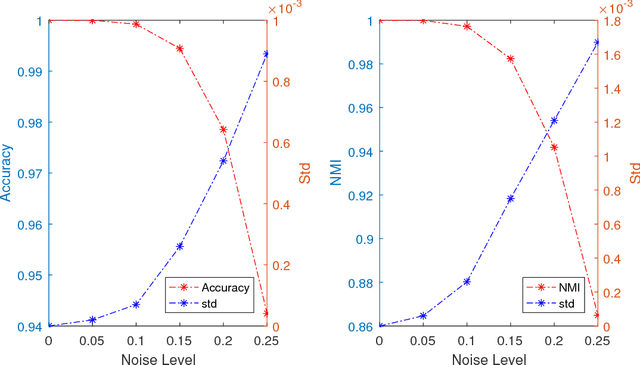
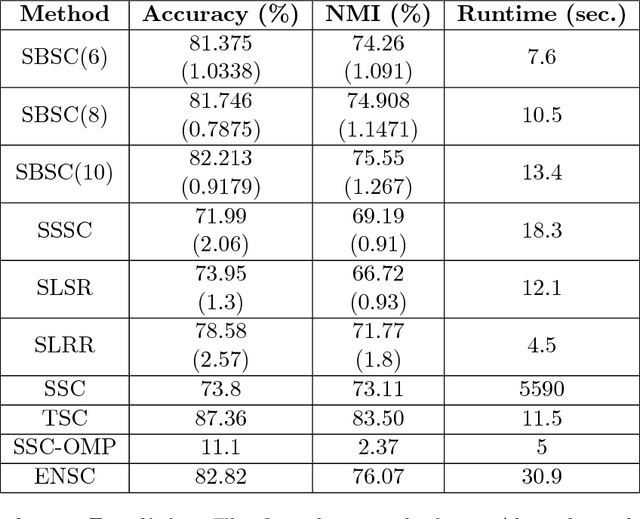
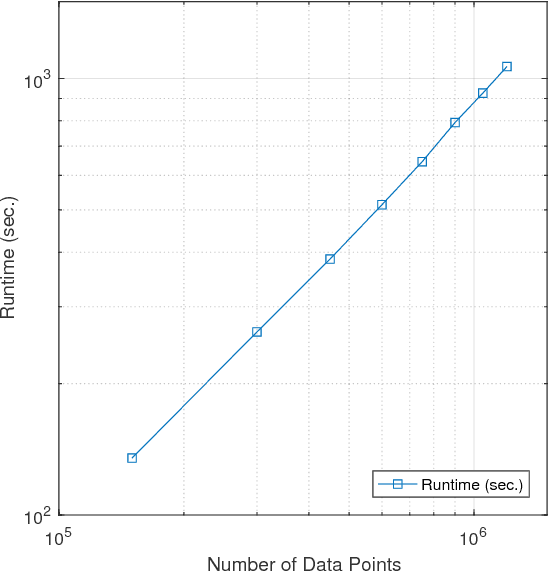
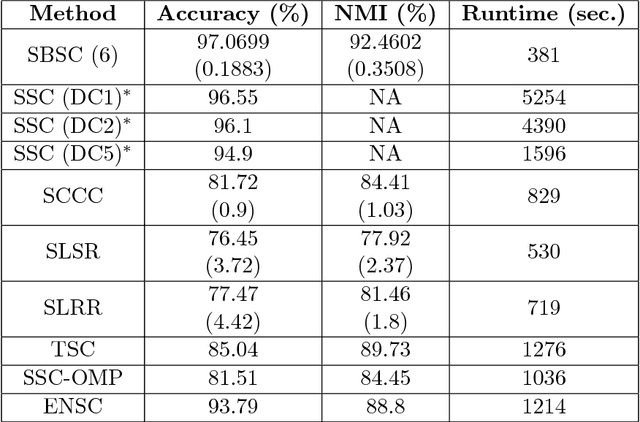
The problem of dimension reduction is of increasing importance in modern data analysis. In this paper, we consider modeling the collection of points in a high dimensional space as a union of low dimensional subspaces. In particular we propose a highly scalable sampling based algorithm that clusters the entire data via first spectral clustering of a small random sample followed by classifying or labeling the remaining out of sample points. The key idea is that this random subset borrows information across the entire data set and that the problem of clustering points can be replaced with the more efficient and robust problem of "clustering sub-clusters". We provide theoretical guarantees for our procedure. The numerical results indicate we outperform other state-of-the-art subspace clustering algorithms with respect to accuracy and speed.

Angle-Based Joint and Individual Variation Explained

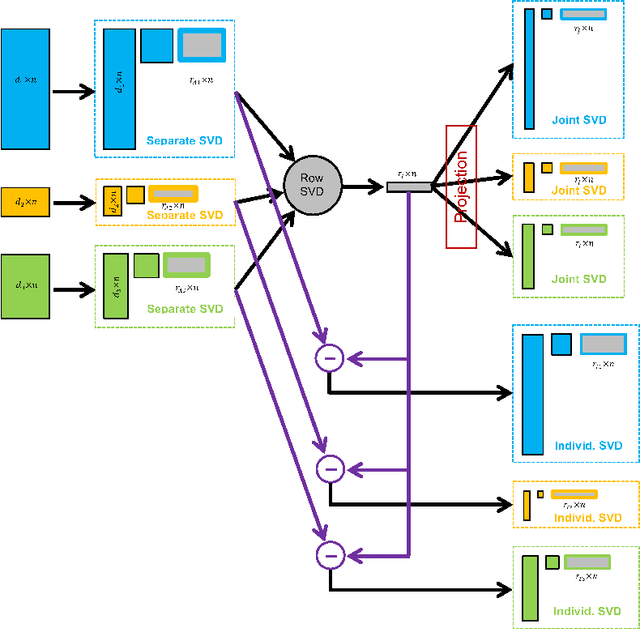
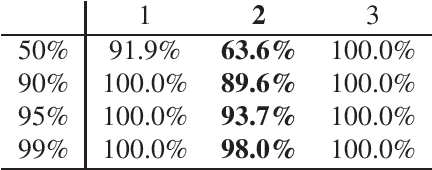
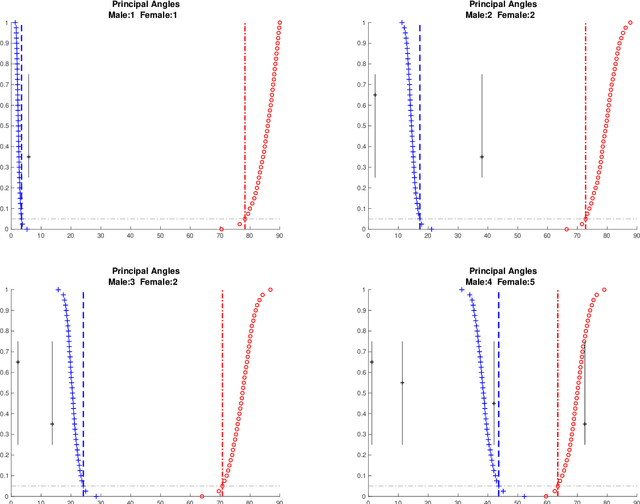
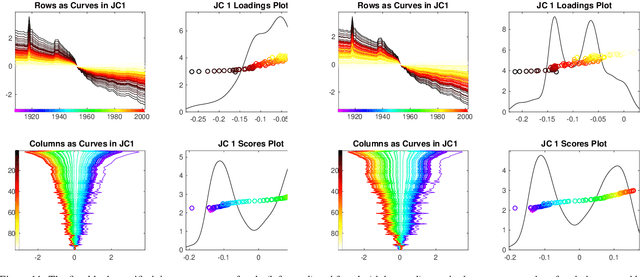
Integrative analysis of disparate data blocks measured on a common set of experimental subjects is a major challenge in modern data analysis. This data structure naturally motivates the simultaneous exploration of the joint and individual variation within each data block resulting in new insights. For instance, there is a strong desire to integrate the multiple genomic data sets in The Cancer Genome Atlas to characterize the common and also the unique aspects of cancer genetics and cell biology for each source. In this paper we introduce Angle-Based Joint and Individual Variation Explained capturing both joint and individual variation within each data block. This is a major improvement over earlier approaches to this challenge in terms of a new conceptual understanding, much better adaption to data heterogeneity and a fast linear algebra computation. Important mathematical contributions are the use of score subspaces as the principal descriptors of variation structure and the use of perturbation theory as the guide for variation segmentation. This leads to an exploratory data analysis method which is insensitive to the heterogeneity among data blocks and does not require separate normalization. An application to cancer data reveals different behaviors of each type of signal in characterizing tumor subtypes. An application to a mortality data set reveals interesting historical lessons. Software and data are available at GitHub <https://github.com/MeileiJiang/AJIVE_Project>.