Deep Fiducial Inference
Paper and Code
Jul 08, 2020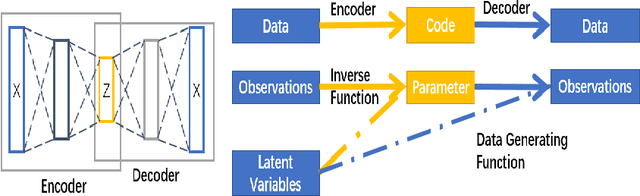

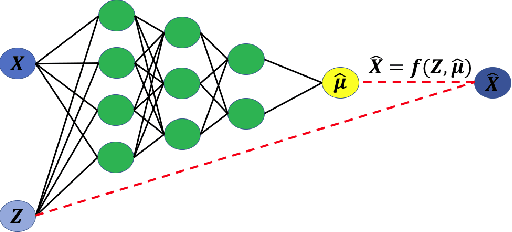
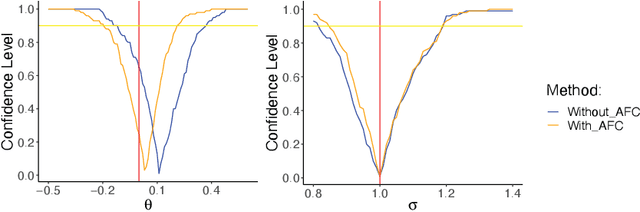
Since the mid-2000s, there has been a resurrection of interest in modern modifications of fiducial inference. To date, the main computational tool to extract a generalized fiducial distribution is Markov chain Monte Carlo (MCMC). We propose an alternative way of computing a generalized fiducial distribution that could be used in complex situations. In particular, to overcome the difficulty when the unnormalized fiducial density (needed for MCMC), we design a fiducial autoencoder (FAE). The fitted autoencoder is used to generate generalized fiducial samples of the unknown parameters. To increase accuracy, we then apply an approximate fiducial computation (AFC) algorithm, by rejecting samples that when plugged into a decoder do not replicate the observed data well enough. Our numerical experiments show the effectiveness of our FAE-based inverse solution and the excellent coverage performance of the AFC corrected FAE solution.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge