Exploring System 1 and 2 communication for latent reasoning in LLMs

Should LLM reasoning live in a separate module, or within a single model's forward pass and representational space? We study dual-architecture latent reasoning, where a fluent Base exchanges latent messages with a Coprocessor, and test two hypotheses aimed at improving latent communication over Liu et al. (2024): (H1) increase channel capacity; (H2) learn communication via joint finetuning. Under matched latent-token budgets on GPT-2 and Qwen-3, H2 is consistently strongest while H1 yields modest gains. A unified soft-embedding baseline, a single model with the same forward pass and shared representations, using the same latent-token budget, nearly matches H2 and surpasses H1, suggesting current dual designs mostly add compute rather than qualitatively improving reasoning. Across GSM8K, ProsQA, and a Countdown stress test with increasing branching factor, scaling the latent-token budget beyond small values fails to improve robustness. Latent analyses show overlapping subspaces with limited specialization, consistent with weak reasoning gains. We conclude dual-model latent reasoning remains promising in principle, but likely requires objectives and communication mechanisms that explicitly shape latent spaces for algorithmic planning.

LLM-Enhanced Dialogue Management for Full-Duplex Spoken Dialogue Systems

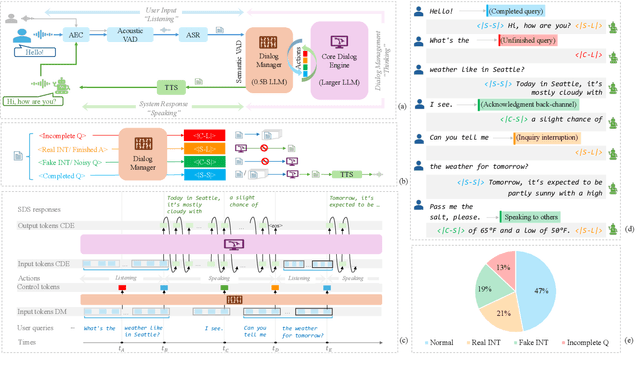
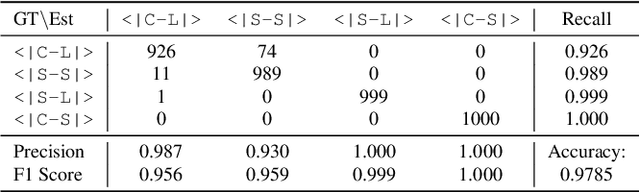
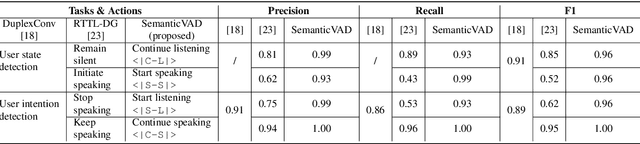
Achieving full-duplex communication in spoken dialogue systems (SDS) requires real-time coordination between listening, speaking, and thinking. This paper proposes a semantic voice activity detection (VAD) module as a dialogue manager (DM) to efficiently manage turn-taking in full-duplex SDS. Implemented as a lightweight (0.5B) LLM fine-tuned on full-duplex conversation data, the semantic VAD predicts four control tokens to regulate turn-switching and turn-keeping, distinguishing between intentional and unintentional barge-ins while detecting query completion for handling user pauses and hesitations. By processing input speech in short intervals, the semantic VAD enables real-time decision-making, while the core dialogue engine (CDE) is only activated for response generation, reducing computational overhead. This design allows independent DM optimization without retraining the CDE, balancing interaction accuracy and inference efficiency for scalable, next-generation full-duplex SDS.

Dynamic Analysis Method for Hidden Dangers in Substation Based on Knowledge Graph

To address the challenge of identifying and understanding hidden dangers in substations from unstructured text data, a novel dynamic analysis method is proposed. This approach begins by analyzing and extracting data from the unstructured text related to hidden dangers. It then leverages a flexible, distributed data search engine built on Elastic-Search to handle this information. Following this, the hidden Markov model is employed to train the data within the engine. The Viterbi algorithm is integrated to decipher the hidden state sequences, facilitating the segmentation and labeling of entities related to hidden dangers. The final step involves using the Neo4j graph database to dynamically create a knowledge map that visualizes hidden dangers in the substation. This method's effectiveness is demonstrated through an example analysis using data from a specific substation's hidden dangers.

Distilling Heterogeneity: From Explanations of Heterogeneous Treatment Effect Models to Interpretable Policies

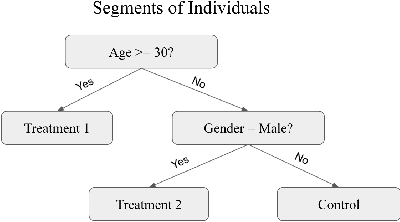
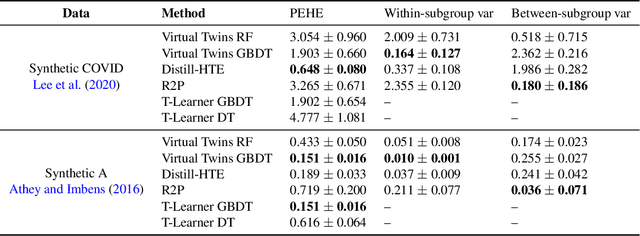
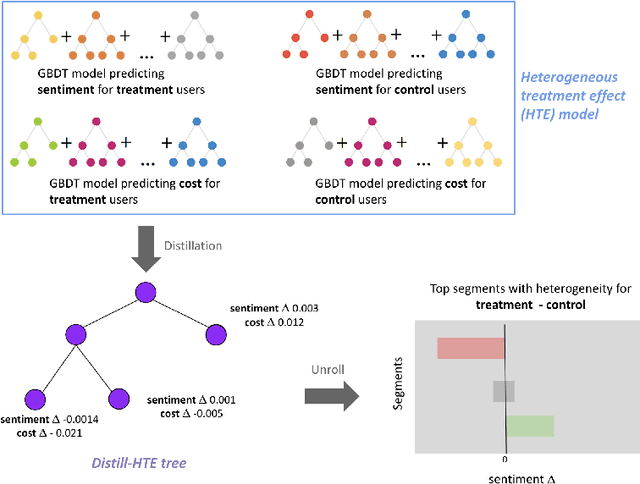
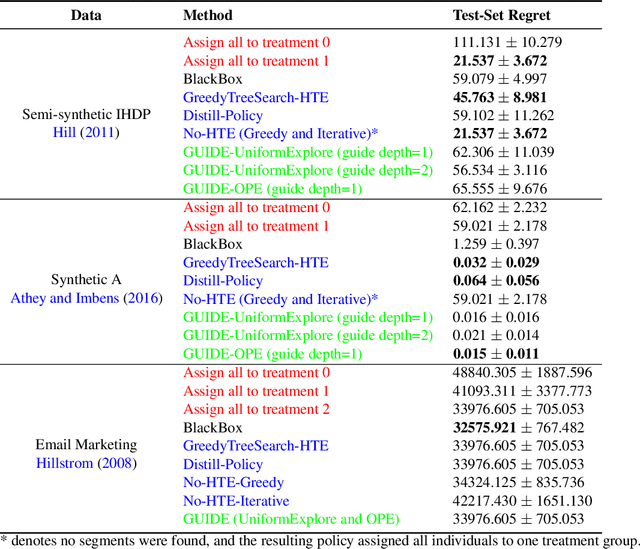
Internet companies are increasingly using machine learning models to create personalized policies which assign, for each individual, the best predicted treatment for that individual. They are frequently derived from black-box heterogeneous treatment effect (HTE) models that predict individual-level treatment effects. In this paper, we focus on (1) learning explanations for HTE models; (2) learning interpretable policies that prescribe treatment assignments. We also propose guidance trees, an approach to ensemble multiple interpretable policies without the loss of interpretability. These rule-based interpretable policies are easy to deploy and avoid the need to maintain a HTE model in a production environment.

Provable Data Clustering via Innovation Search

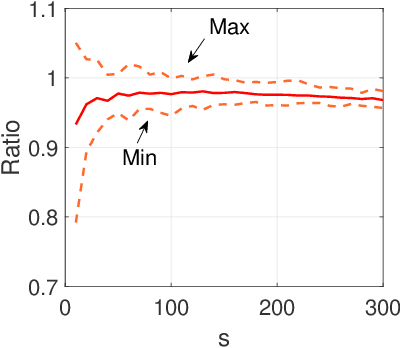
This paper studies the subspace clustering problem in which data points collected from high-dimensional ambient space lie in a union of linear subspaces. Subspace clustering becomes challenging when the dimension of intersection between subspaces is large and most of the self-representation based methods are sensitive to the intersection between the span of clusters. In sharp contrast to the self-representation based methods, a recently proposed clustering method termed Innovation Pursuit, computed a set of optimal directions (directions of innovation) to build the adjacency matrix. This paper focuses on the Innovation Pursuit Algorithm to shed light on its impressive performance when the subspaces are heavily intersected. It is shown that in contrast to most of the existing methods which require the subspaces to be sufficiently incoherent with each other, Innovation Pursuit only requires the innovative components of the subspaces to be sufficiently incoherent with each other. These new sufficient conditions allow the clusters to be strongly close to each other. Motivated by the presented theoretical analysis, a simple yet effective projection based technique is proposed which we show with both numerical and theoretical results that it can boost the performance of Innovation Pursuit.

A Note on Optimal Sampling Strategy for Structural Variant Detection Using Optical Mapping

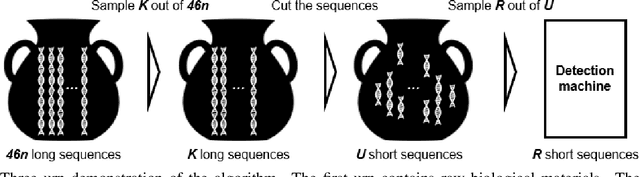
Structural variants compose the majority of human genetic variation, but are difficult to assess using current genomic sequencing technologies. Optical mapping technologies, which measure the size of chromosomal fragments between labeled markers, offer an alternative approach. As these technologies mature towards becoming clinical tools, there is a need to develop an approach for determining the optimal strategy for sampling biological material in order to detect a variant at some threshold. Here we develop an optimization approach using a simple, yet realistic, model of the genomic mapping process using a hyper-geometric distribution and {probabilistic} concentration inequalities. Our approach is both computationally and analytically tractable and includes a novel approach to getting tail bounds of hyper-geometric distribution. We show that if a genomic mapping technology can sample most of the chromosomal fragments within a sample, comparatively little biological material is needed to detect a variant at high confidence.

Subspace Clustering through Sub-Clusters

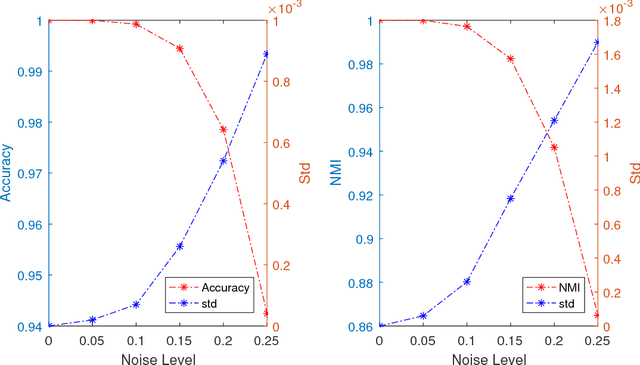
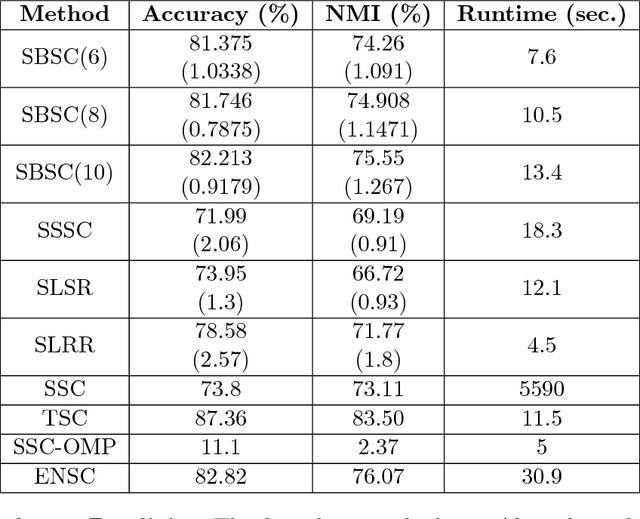
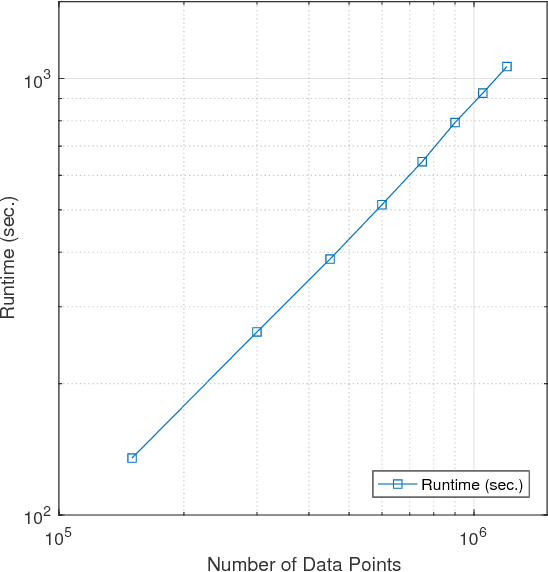
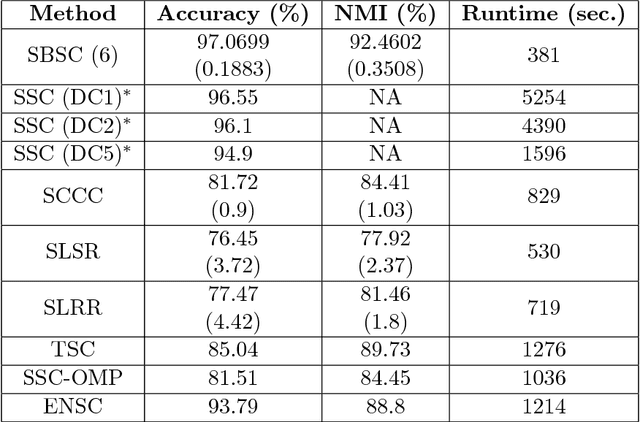
The problem of dimension reduction is of increasing importance in modern data analysis. In this paper, we consider modeling the collection of points in a high dimensional space as a union of low dimensional subspaces. In particular we propose a highly scalable sampling based algorithm that clusters the entire data via first spectral clustering of a small random sample followed by classifying or labeling the remaining out of sample points. The key idea is that this random subset borrows information across the entire data set and that the problem of clustering points can be replaced with the more efficient and robust problem of "clustering sub-clusters". We provide theoretical guarantees for our procedure. The numerical results indicate we outperform other state-of-the-art subspace clustering algorithms with respect to accuracy and speed.