Subspace Clustering through Sub-Clusters
Paper and Code
Nov 15, 2018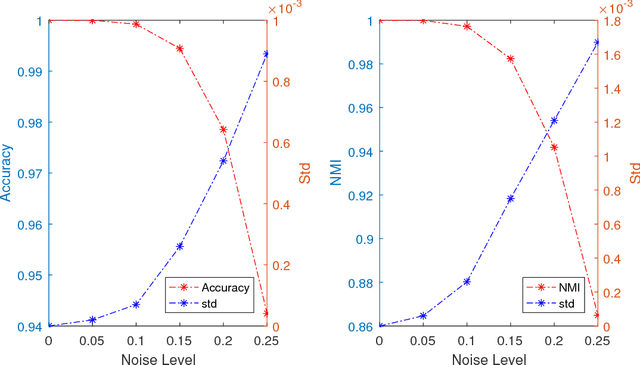
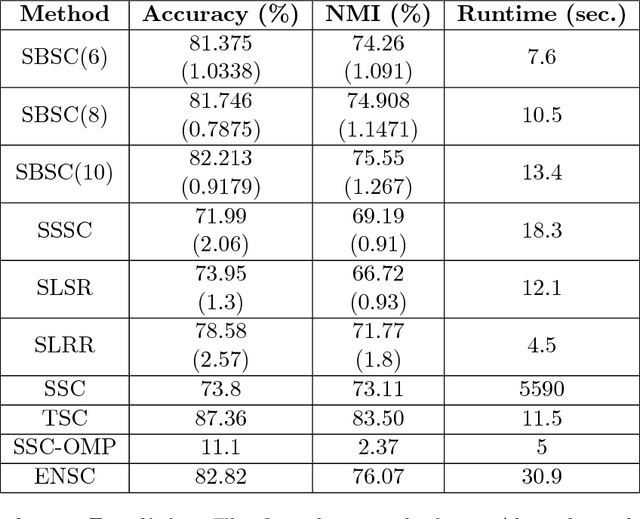
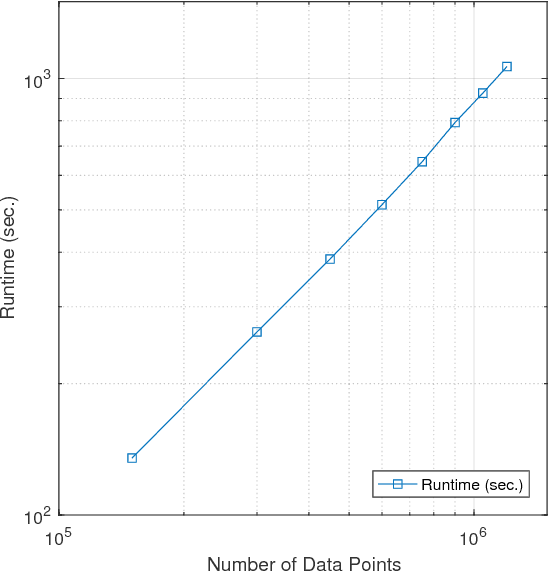
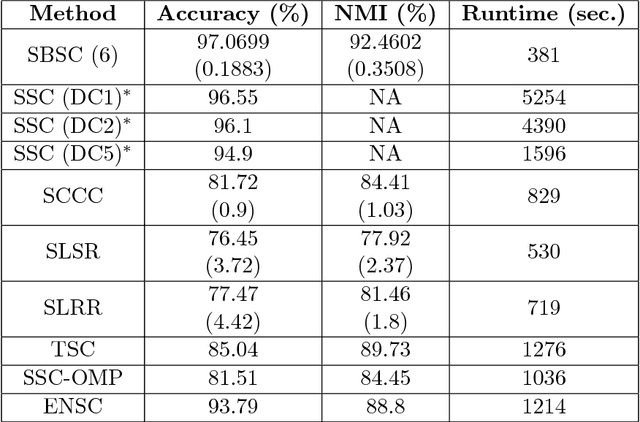
The problem of dimension reduction is of increasing importance in modern data analysis. In this paper, we consider modeling the collection of points in a high dimensional space as a union of low dimensional subspaces. In particular we propose a highly scalable sampling based algorithm that clusters the entire data via first spectral clustering of a small random sample followed by classifying or labeling the remaining out of sample points. The key idea is that this random subset borrows information across the entire data set and that the problem of clustering points can be replaced with the more efficient and robust problem of "clustering sub-clusters". We provide theoretical guarantees for our procedure. The numerical results indicate we outperform other state-of-the-art subspace clustering algorithms with respect to accuracy and speed.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge