J. S. Marron
Region of Interest Detection in Melanocytic Skin Tumor Whole Slide Images
Oct 29, 2022Abstract:Automated region of interest detection in histopathological image analysis is a challenging and important topic with tremendous potential impact on clinical practice. The deep-learning methods used in computational pathology help us to reduce costs and increase the speed and accuracy of regions of interest detection and cancer diagnosis. In this work, we propose a patch-based region of interest detection method for melanocytic skin tumor whole-slide images. We work with a dataset that contains 165 primary melanomas and nevi Hematoxylin and Eosin whole-slide images and build a deep-learning method. The proposed method performs well on a hold-out test data set including five TCGA-SKCM slides (accuracy of 93.94\% in slide classification task and intersection over union rate of 41.27\% in the region of interest detection task), showing the outstanding performance of our model on melanocytic skin tumor. Even though we test the experiments on the skin tumor dataset, our work could also be extended to other medical image detection problems, such as various tumors' classification and prediction, to help and benefit the clinical evaluation and diagnosis of different tumors.
Non-Euclidean Analysis of Joint Variations in Multi-Object Shapes
Sep 07, 2021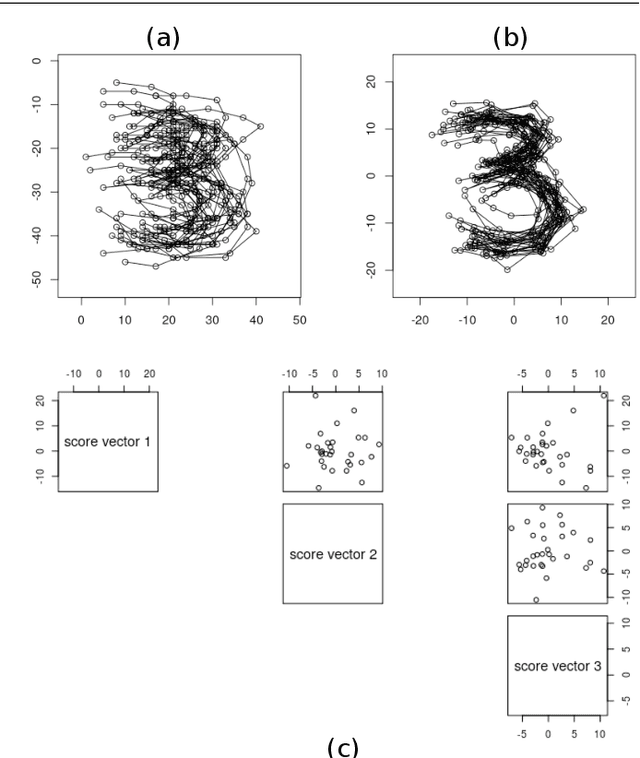

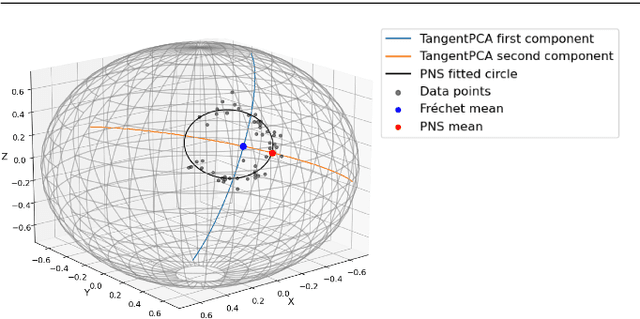
Abstract:This paper considers joint analysis of multiple functionally related structures in classification tasks. In particular, our method developed is driven by how functionally correlated brain structures vary together between autism and control groups. To do so, we devised a method based on a novel combination of (1) non-Euclidean statistics that can faithfully represent non-Euclidean data in Euclidean spaces and (2) a non-parametric integrative analysis method that can decompose multi-block Euclidean data into joint, individual, and residual structures. We find that the resulting joint structure is effective, robust, and interpretable in recognizing the underlying patterns of the joint variation of multi-block non-Euclidean data. We verified the method in classifying the structural shape data collected from cases that developed and did not develop into Autistic Spectrum Disorder (ASD).
Visual High Dimensional Hypothesis Testing
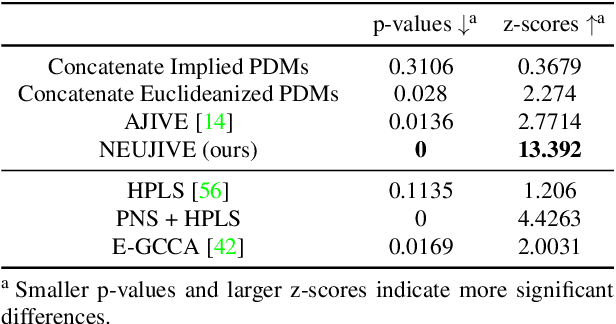
Jan 02, 2021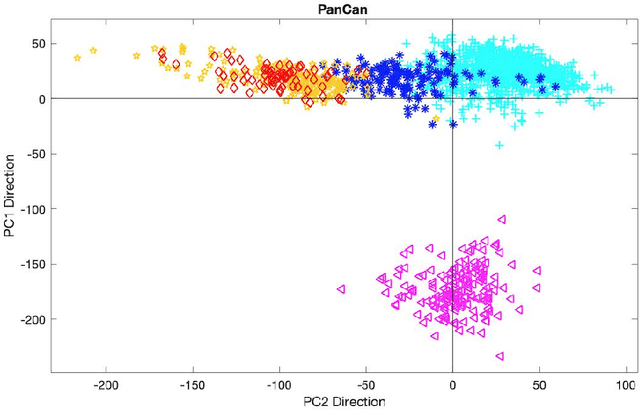
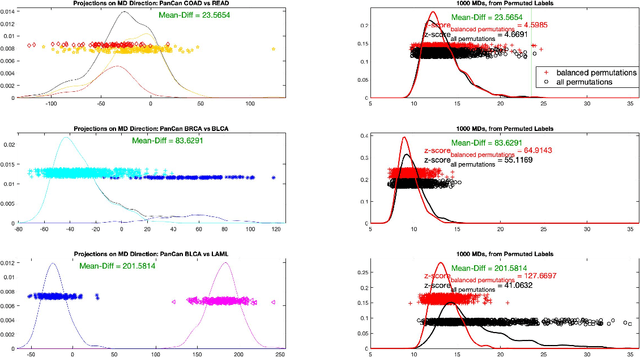
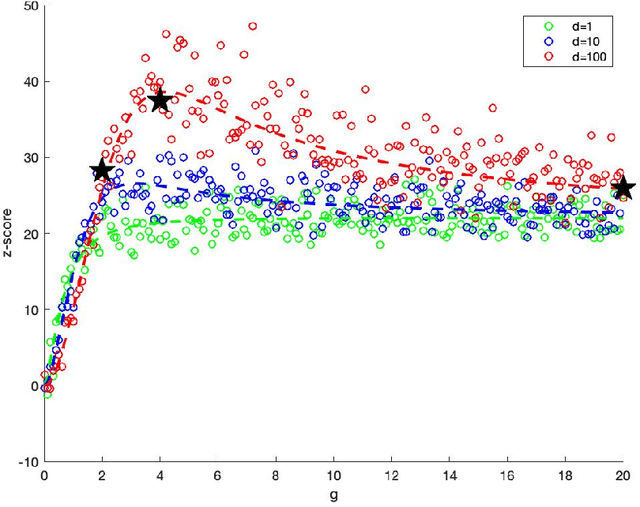
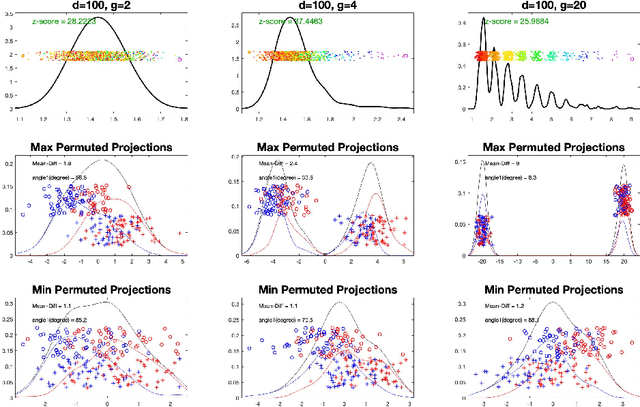
Abstract:In exploratory data analysis of known classes of high dimensional data, a central question is how distinct are the classes? The Direction Projection Permutation (DiProPerm) hypothesis test provides an answer to this that is directly connected to a visual analysis of the data. In this paper, we propose an improved DiProPerm test that solves 3 major challenges of the original version. First, we implement only balanced permutations to increase the test power for data with strong signals. Second, our mathematical analysis leads to an adjustment to correct the null behavior of both balanced and the conventional all permutations. Third, new confidence intervals (reflecting permutation variation) for test significance are also proposed for comparison of results across different contexts. This improvement of DiProPerm inference is illustrated in the context of comparing cancer types in examples from The Cancer Genome Atlas.
diproperm: An R Package for the DiProPerm Test
Aug 30, 2020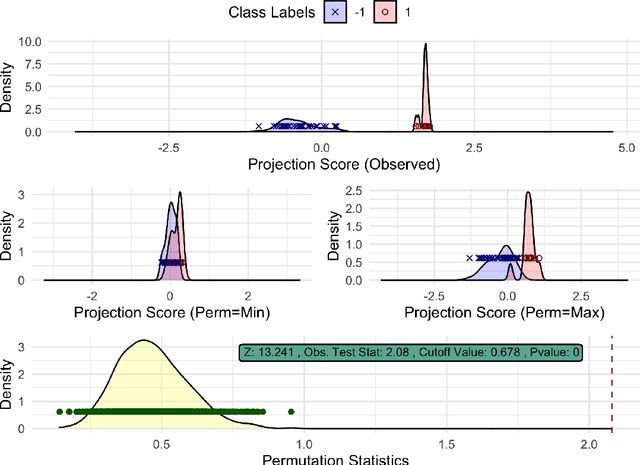
Abstract:High-dimensional low sample size (HDLSS) data sets emerge frequently in many biomedical applications. A common task for analyzing HDLSS data is to assign data to the correct class using a classifier. Classifiers which use two labels and a linear combination of features are known as binary linear classifiers. The direction-projection-permutation (DiProPerm) test was developed for testing the difference of two high-dimensional distributions induced by a binary linear classifier. This paper discusses the key components of the DiProPerm test, introduces the diproperm R package, and demonstrates the package on a real-world data set.
Deep Multi-View Learning via Task-Optimal CCA
Jul 17, 2019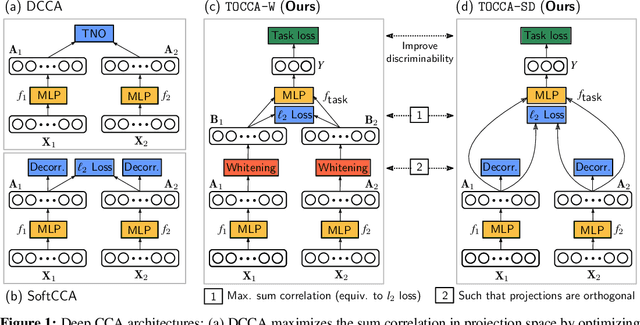

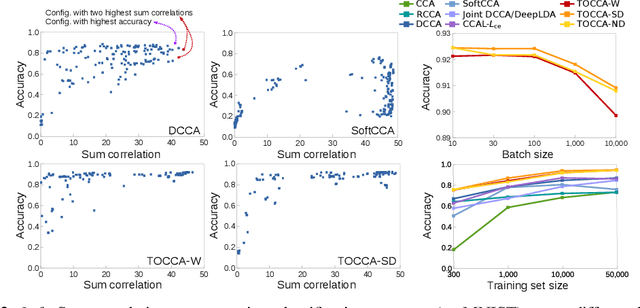

Abstract:Canonical Correlation Analysis (CCA) is widely used for multimodal data analysis and, more recently, for discriminative tasks such as multi-view learning; however, it makes no use of class labels. Recent CCA methods have started to address this weakness but are limited in that they do not simultaneously optimize the CCA projection for discrimination and the CCA projection itself, or they are linear only. We address these deficiencies by simultaneously optimizing a CCA-based and a task objective in an end-to-end manner. Together, these two objectives learn a non-linear CCA projection to a shared latent space that is highly correlated and discriminative. Our method shows a significant improvement over previous state-of-the-art (including deep supervised approaches) for cross-view classification, regularization with a second view, and semi-supervised learning on real data.
Geometric Insights into Support Vector Machine Behavior using the KKT Conditions
Oct 10, 2018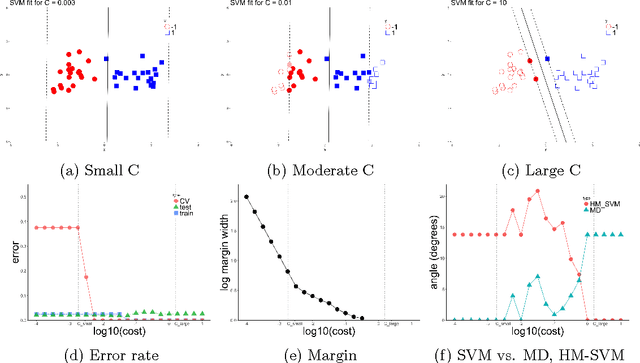
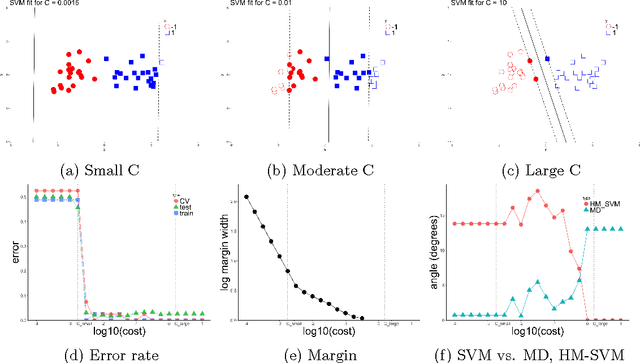
Abstract:The support vector machine (SVM) is a powerful and widely used classification algorithm. This paper uses the Karush-Kuhn-Tucker conditions to provide rigorous mathematical proof for new insights into the behavior of SVM. These insights provide perhaps unexpected relationships between SVM and two other linear classifiers: the mean difference and the maximal data piling direction. For example, we show that in many cases SVM can be viewed as a cropped version of these classifiers. By carefully exploring these connections we show how SVM tuning behavior is affected by characteristics including: balanced vs. unbalanced classes, low vs. high dimension, separable vs. non-separable data. These results provide further insights into tuning SVM via cross-validation by explaining observed pathological behavior and motivating improved cross-validation methodology. Finally, we also provide new results on the geometry of complete data piling directions in high dimensional space.
Multiple Instance Learning for Heterogeneous Images: Training a CNN for Histopathology
Jun 13, 2018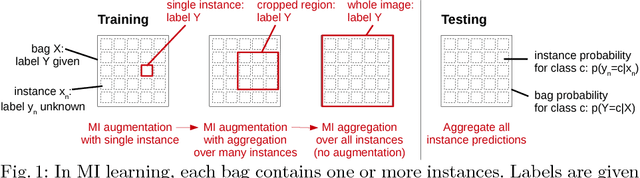
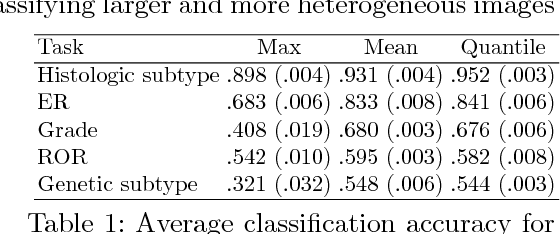
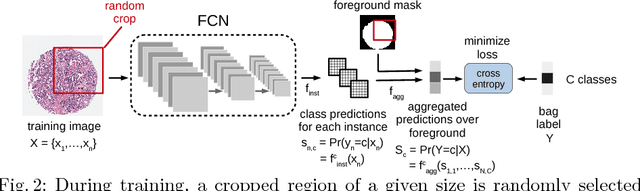
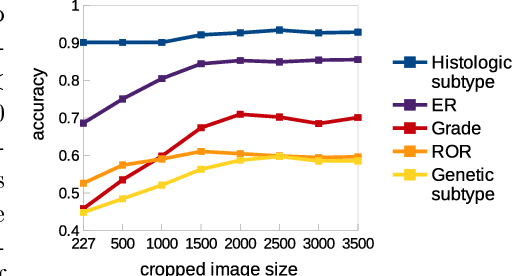
Abstract:Multiple instance (MI) learning with a convolutional neural network enables end-to-end training in the presence of weak image-level labels. We propose a new method for aggregating predictions from smaller regions of the image into an image-level classification by using the quantile function. The quantile function provides a more complete description of the heterogeneity within each image, improving image-level classification. We also adapt image augmentation to the MI framework by randomly selecting cropped regions on which to apply MI aggregation during each epoch of training. This provides a mechanism to study the importance of MI learning. We validate our method on five different classification tasks for breast tumor histology and provide a visualization method for interpreting local image classifications that could lead to future insights into tumor heterogeneity.
Angle-Based Joint and Individual Variation Explained
Mar 18, 2018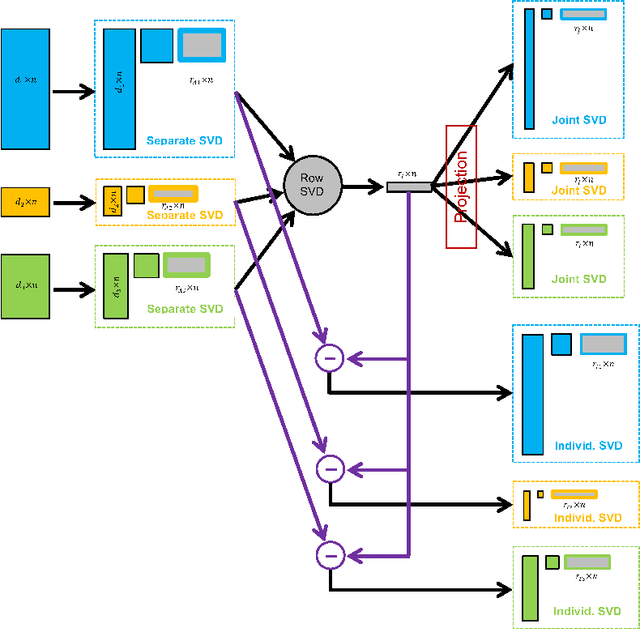
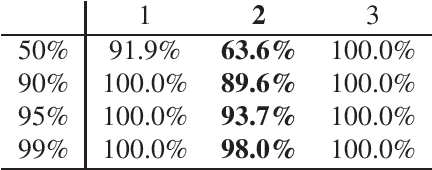
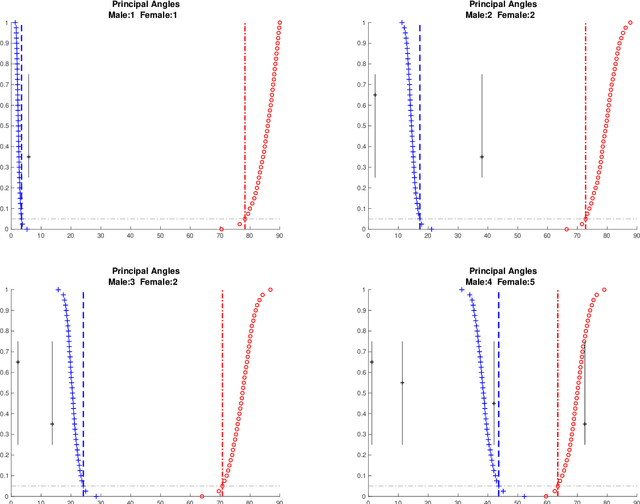
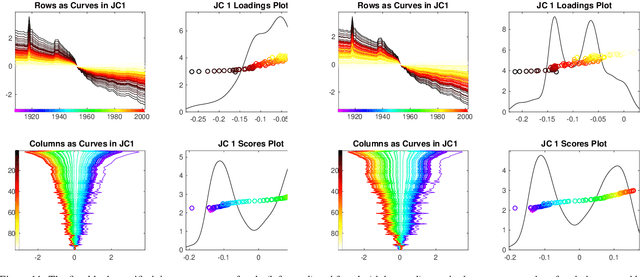
Abstract:Integrative analysis of disparate data blocks measured on a common set of experimental subjects is a major challenge in modern data analysis. This data structure naturally motivates the simultaneous exploration of the joint and individual variation within each data block resulting in new insights. For instance, there is a strong desire to integrate the multiple genomic data sets in The Cancer Genome Atlas to characterize the common and also the unique aspects of cancer genetics and cell biology for each source. In this paper we introduce Angle-Based Joint and Individual Variation Explained capturing both joint and individual variation within each data block. This is a major improvement over earlier approaches to this challenge in terms of a new conceptual understanding, much better adaption to data heterogeneity and a fast linear algebra computation. Important mathematical contributions are the use of score subspaces as the principal descriptors of variation structure and the use of perturbation theory as the guide for variation segmentation. This leads to an exploratory data analysis method which is insensitive to the heterogeneity among data blocks and does not require separate normalization. An application to cancer data reveals different behaviors of each type of signal in characterizing tumor subtypes. An application to a mortality data set reveals interesting historical lessons. Software and data are available at GitHub <https://github.com/MeileiJiang/AJIVE_Project>.
Distance weighted discrimination of face images for gender classification
Jun 15, 2017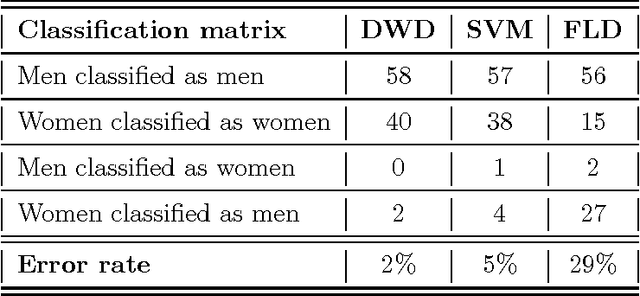
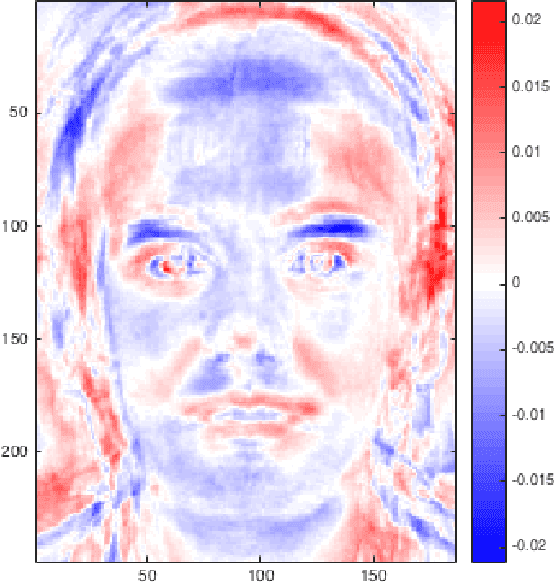
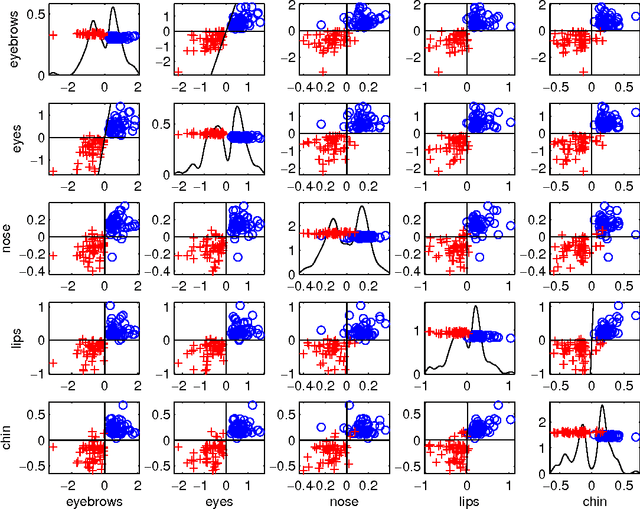
Abstract:We illustrate the advantages of distance weighted discrimination for classification and feature extraction in a High Dimension Low Sample Size (HDLSS) situation. The HDLSS context is a gender classification problem of face images in which the dimension of the data is several orders of magnitude larger than the sample size. We compare distance weighted discrimination with Fisher's linear discriminant, support vector machines, and principal component analysis by exploring their classification interpretation through insightful visuanimations and by examining the classifiers' discriminant errors. This analysis enables us to make new contributions to the understanding of the drivers of human discrimination between males and females.
Large-Margin Classification with Multiple Decision Rules
Nov 19, 2014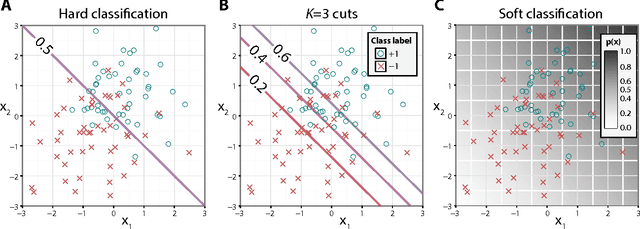
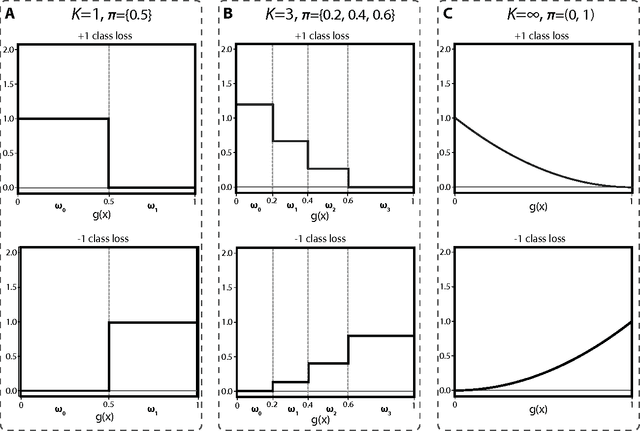
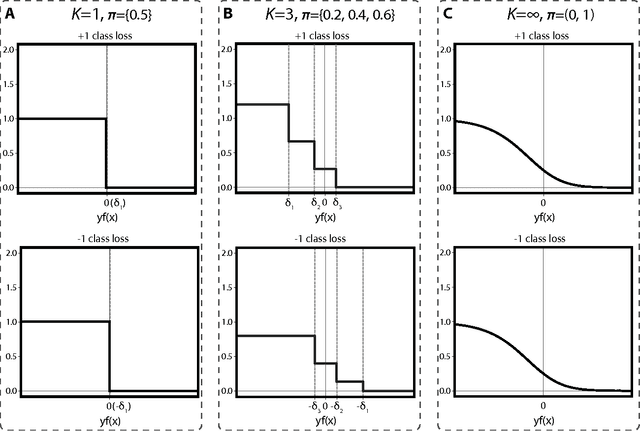
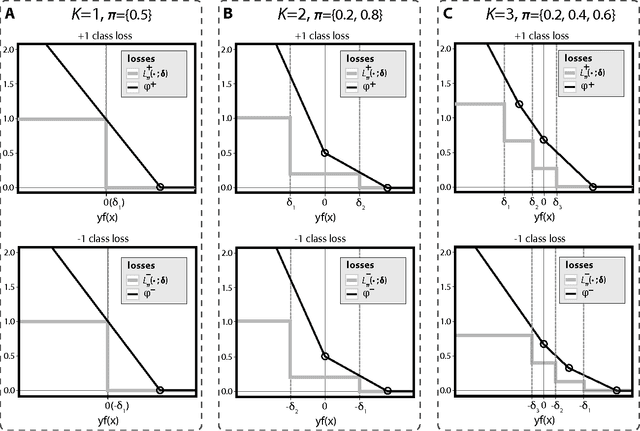
Abstract:Binary classification is a common statistical learning problem in which a model is estimated on a set of covariates for some outcome indicating the membership of one of two classes. In the literature, there exists a distinction between hard and soft classification. In soft classification, the conditional class probability is modeled as a function of the covariates. In contrast, hard classification methods only target the optimal prediction boundary. While hard and soft classification methods have been studied extensively, not much work has been done to compare the actual tasks of hard and soft classification. In this paper we propose a spectrum of statistical learning problems which span the hard and soft classification tasks based on fitting multiple decision rules to the data. By doing so, we reveal a novel collection of learning tasks of increasing complexity. We study the problems using the framework of large-margin classifiers and a class of piecewise linear convex surrogates, for which we derive statistical properties and a corresponding sub-gradient descent algorithm. We conclude by applying our approach to simulation settings and a magnetic resonance imaging (MRI) dataset from the Alzheimer's Disease Neuroimaging Initiative (ADNI) study.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge