Geometric Insights into Support Vector Machine Behavior using the KKT Conditions
Paper and Code
Oct 10, 2018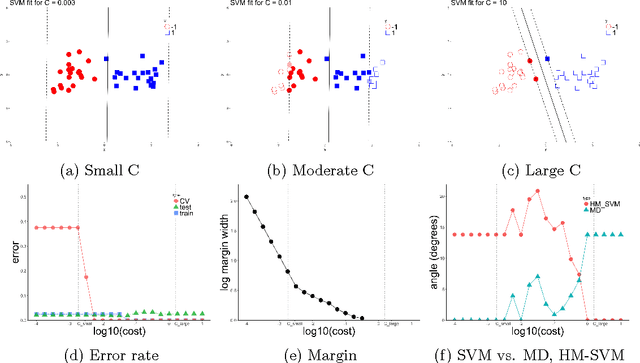
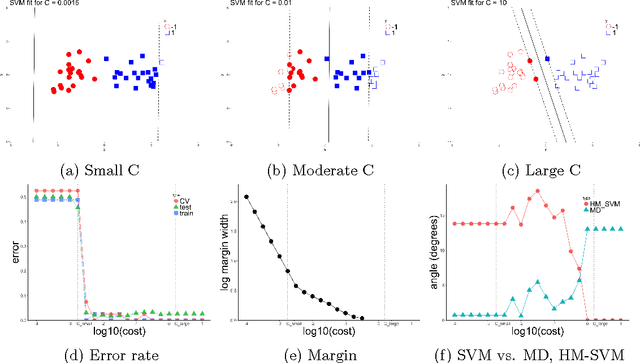
The support vector machine (SVM) is a powerful and widely used classification algorithm. This paper uses the Karush-Kuhn-Tucker conditions to provide rigorous mathematical proof for new insights into the behavior of SVM. These insights provide perhaps unexpected relationships between SVM and two other linear classifiers: the mean difference and the maximal data piling direction. For example, we show that in many cases SVM can be viewed as a cropped version of these classifiers. By carefully exploring these connections we show how SVM tuning behavior is affected by characteristics including: balanced vs. unbalanced classes, low vs. high dimension, separable vs. non-separable data. These results provide further insights into tuning SVM via cross-validation by explaining observed pathological behavior and motivating improved cross-validation methodology. Finally, we also provide new results on the geometry of complete data piling directions in high dimensional space.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge