Understanding complex predictive models with Ghost Variables

We propose a procedure for assigning a relevance measure to each explanatory variable in a complex predictive model. We assume that we have a training set to fit the model and a test set to check the out of sample performance. First, the individual relevance of each variable is computed by comparing the predictions in the test set, given by the model that includes all the variables with those of another model in which the variable of interest is substituted by its ghost variable, defined as the prediction of this variable by using the rest of explanatory variables. Second, we check the joint effects among the variables by using the eigenvalues of a relevance matrix that is the covariance matrix of the vectors of individual effects. It is shown that in simple models, as linear or additive models, the proposed measures are related to standard measures of significance of the variables and in neural networks models (and in other algorithmic prediction models) the procedure provides information about the joint and individual effects of the variables that is not usually available by other methods. The procedure is illustrated with simulated examples and the analysis of a large real data set.

Distance weighted discrimination of face images for gender classification

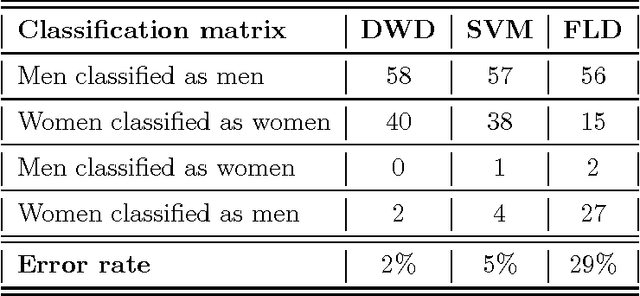
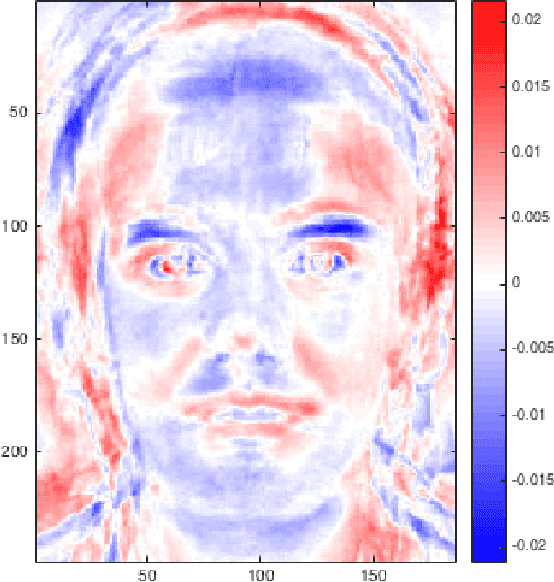
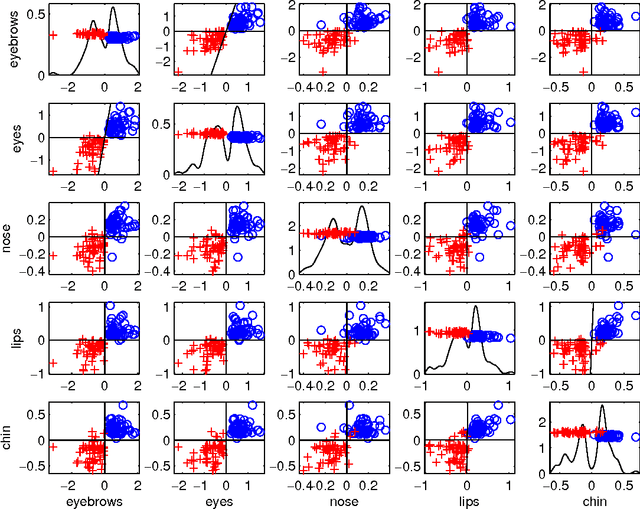
We illustrate the advantages of distance weighted discrimination for classification and feature extraction in a High Dimension Low Sample Size (HDLSS) situation. The HDLSS context is a gender classification problem of face images in which the dimension of the data is several orders of magnitude larger than the sample size. We compare distance weighted discrimination with Fisher's linear discriminant, support vector machines, and principal component analysis by exploring their classification interpretation through insightful visuanimations and by examining the classifiers' discriminant errors. This analysis enables us to make new contributions to the understanding of the drivers of human discrimination between males and females.