Satisficing Exploration in Bandit Optimization

Motivated by the concept of satisficing in decision-making, we consider the problem of satisficing exploration in bandit optimization. In this setting, the learner aims at selecting satisficing arms (arms with mean reward exceeding a certain threshold value) as frequently as possible. The performance is measured by satisficing regret, which is the cumulative deficit of the chosen arm's mean reward compared to the threshold. We propose SELECT, a general algorithmic template for Satisficing Exploration via LowEr Confidence bound Testing, that attains constant satisficing regret for a wide variety of bandit optimization problems in the realizable case (i.e., a satisficing arm exists). Specifically, given a class of bandit optimization problems and a corresponding learning oracle with sub-linear (standard) regret upper bound, SELECT iteratively makes use of the oracle to identify a potential satisficing arm with low regret. Then, it collects data samples from this arm, and continuously compares the LCB of the identified arm's mean reward against the threshold value to determine if it is a satisficing arm. As a complement, SELECT also enjoys the same (standard) regret guarantee as the oracle in the non-realizable case. Finally, we conduct numerical experiments to validate the performance of SELECT for several popular bandit optimization settings.

Phase Transitions in Learning and Earning under Price Protection Guarantee

Motivated by the prevalence of ``price protection guarantee", which allows a customer who purchased a product in the past to receive a refund from the seller during the so-called price protection period (typically defined as a certain time window after the purchase date) in case the seller decides to lower the price, we study the impact of such policy on the design of online learning algorithm for data-driven dynamic pricing with initially unknown customer demand. We consider a setting where a firm sells a product over a horizon of $T$ time steps. For this setting, we characterize how the value of $M$, the length of price protection period, can affect the optimal regret of the learning process. We show that the optimal regret is $\tilde{\Theta}(\sqrt{T}+\min\{M,\,T^{2/3}\})$ by first establishing a fundamental impossible regime with novel regret lower bound instances. Then, we propose LEAP, a phased exploration type algorithm for \underline{L}earning and \underline{EA}rning under \underline{P}rice Protection to match this lower bound up to logarithmic factors or even doubly logarithmic factors (when there are only two prices available to the seller). Our results reveal the surprising phase transitions of the optimal regret with respect to $M$. Specifically, when $M$ is not too large, the optimal regret has no major difference when compared to that of the classic setting with no price protection guarantee. We also show that there exists an upper limit on how much the optimal regret can deteriorate when $M$ grows large. Finally, we conduct extensive numerical experiments to show the benefit of LEAP over other heuristic methods for this problem.

Sparse Bayesian Optimization

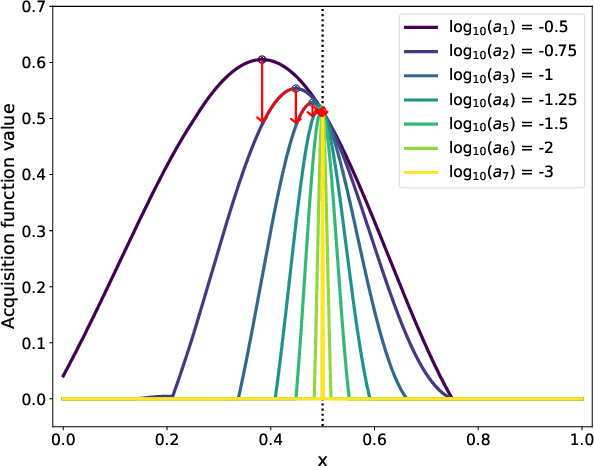
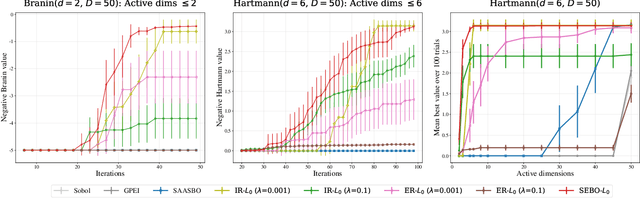
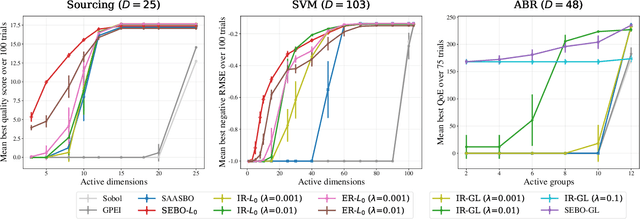
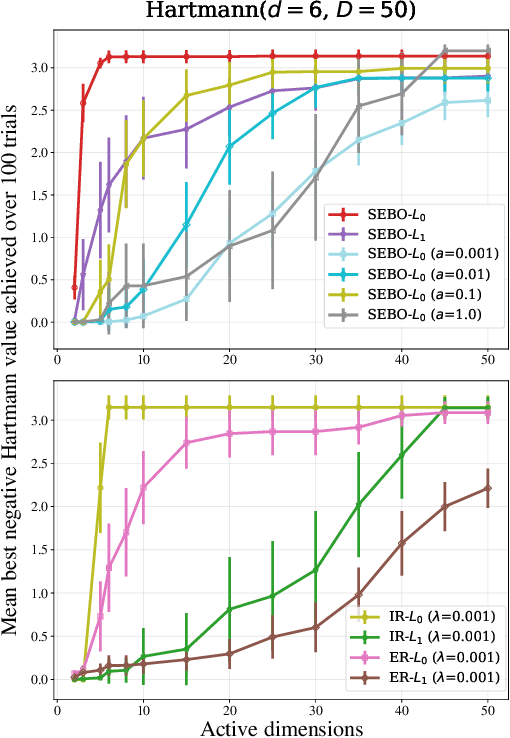
Bayesian optimization (BO) is a powerful approach to sample-efficient optimization of black-box objective functions. However, the application of BO to areas such as recommendation systems often requires taking the interpretability and simplicity of the configurations into consideration, a setting that has not been previously studied in the BO literature. To make BO applicable in this setting, we present several regularization-based approaches that allow us to discover sparse and more interpretable configurations. We propose a novel differentiable relaxation based on homotopy continuation that makes it possible to target sparsity by working directly with $L_0$ regularization. We identify failure modes for regularized BO and develop a hyperparameter-free method, sparsity exploring Bayesian optimization (SEBO) that seeks to simultaneously maximize a target objective and sparsity. SEBO and methods based on fixed regularization are evaluated on synthetic and real-world problems, and we show that we are able to efficiently optimize for sparsity.

Optimizing High-Dimensional Physics Simulations via Composite Bayesian Optimization

Physical simulation-based optimization is a common task in science and engineering. Many such simulations produce image- or tensor-based outputs where the desired objective is a function of those outputs, and optimization is performed over a high-dimensional parameter space. We develop a Bayesian optimization method leveraging tensor-based Gaussian process surrogates and trust region Bayesian optimization to effectively model the image outputs and to efficiently optimize these types of simulations, including a radio-frequency tower configuration problem and an optical design problem.

Angle-Based Joint and Individual Variation Explained

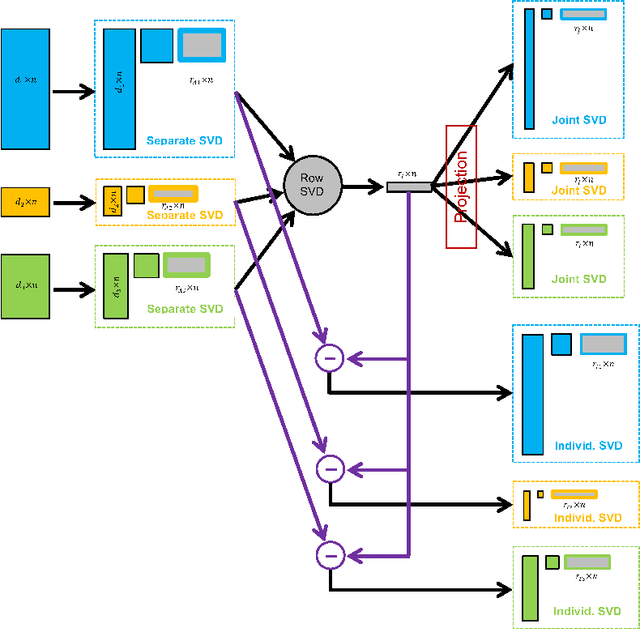
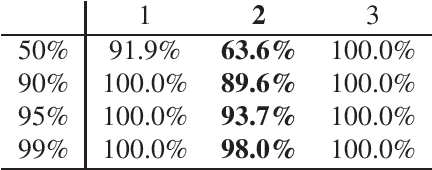
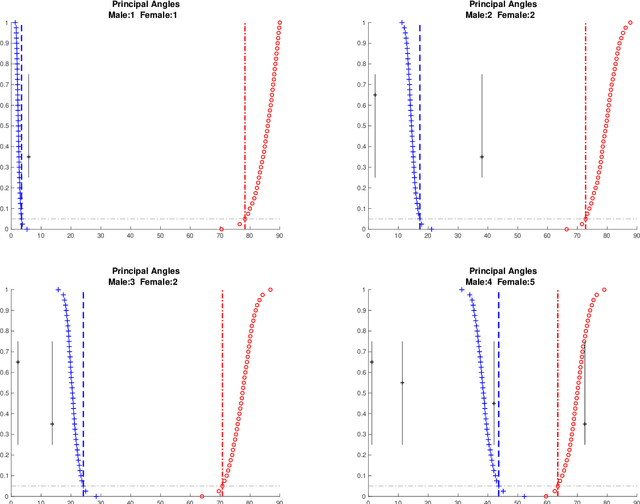
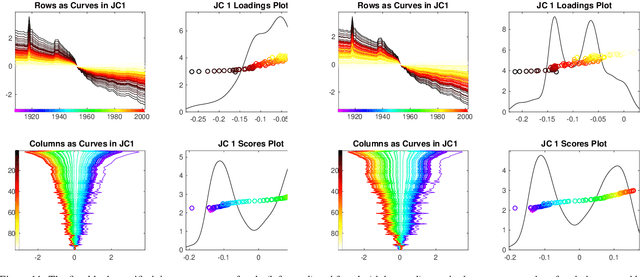
Integrative analysis of disparate data blocks measured on a common set of experimental subjects is a major challenge in modern data analysis. This data structure naturally motivates the simultaneous exploration of the joint and individual variation within each data block resulting in new insights. For instance, there is a strong desire to integrate the multiple genomic data sets in The Cancer Genome Atlas to characterize the common and also the unique aspects of cancer genetics and cell biology for each source. In this paper we introduce Angle-Based Joint and Individual Variation Explained capturing both joint and individual variation within each data block. This is a major improvement over earlier approaches to this challenge in terms of a new conceptual understanding, much better adaption to data heterogeneity and a fast linear algebra computation. Important mathematical contributions are the use of score subspaces as the principal descriptors of variation structure and the use of perturbation theory as the guide for variation segmentation. This leads to an exploratory data analysis method which is insensitive to the heterogeneity among data blocks and does not require separate normalization. An application to cancer data reveals different behaviors of each type of signal in characterizing tumor subtypes. An application to a mortality data set reveals interesting historical lessons. Software and data are available at GitHub <https://github.com/MeileiJiang/AJIVE_Project>.