Phase Transitions in Learning and Earning under Price Protection Guarantee

Motivated by the prevalence of ``price protection guarantee", which allows a customer who purchased a product in the past to receive a refund from the seller during the so-called price protection period (typically defined as a certain time window after the purchase date) in case the seller decides to lower the price, we study the impact of such policy on the design of online learning algorithm for data-driven dynamic pricing with initially unknown customer demand. We consider a setting where a firm sells a product over a horizon of $T$ time steps. For this setting, we characterize how the value of $M$, the length of price protection period, can affect the optimal regret of the learning process. We show that the optimal regret is $\tilde{\Theta}(\sqrt{T}+\min\{M,\,T^{2/3}\})$ by first establishing a fundamental impossible regime with novel regret lower bound instances. Then, we propose LEAP, a phased exploration type algorithm for \underline{L}earning and \underline{EA}rning under \underline{P}rice Protection to match this lower bound up to logarithmic factors or even doubly logarithmic factors (when there are only two prices available to the seller). Our results reveal the surprising phase transitions of the optimal regret with respect to $M$. Specifically, when $M$ is not too large, the optimal regret has no major difference when compared to that of the classic setting with no price protection guarantee. We also show that there exists an upper limit on how much the optimal regret can deteriorate when $M$ grows large. Finally, we conduct extensive numerical experiments to show the benefit of LEAP over other heuristic methods for this problem.

Self-adapting Robustness in Demand Learning

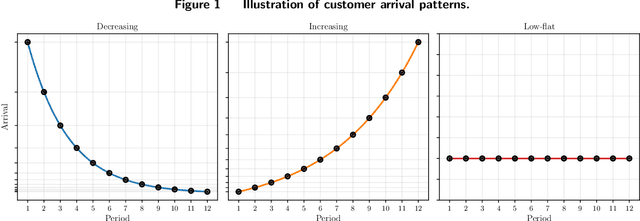
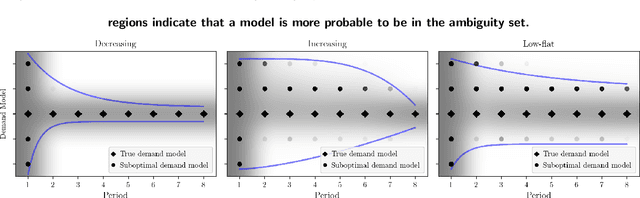
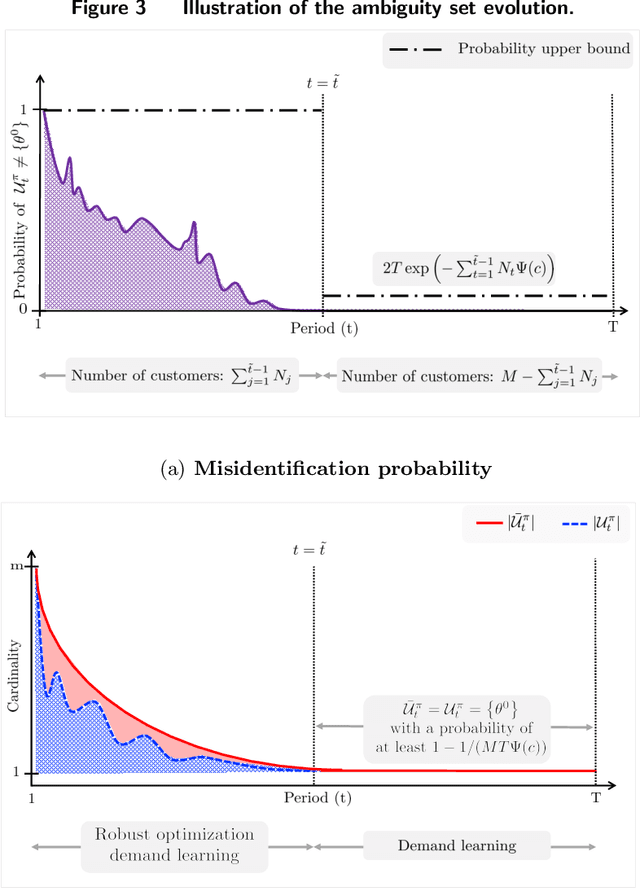
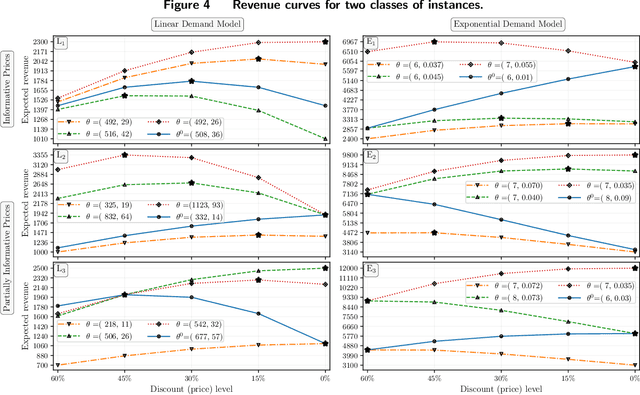
We study dynamic pricing over a finite number of periods in the presence of demand model ambiguity. Departing from the typical no-regret learning environment, where price changes are allowed at any time, pricing decisions are made at pre-specified points in time and each price can be applied to a large number of arrivals. In this environment, which arises in retailing, a pricing decision based on an incorrect demand model can significantly impact cumulative revenue. We develop an adaptively-robust-learning (ARL) pricing policy that learns the true model parameters from the data while actively managing demand model ambiguity. It optimizes an objective that is robust with respect to a self-adapting set of demand models, where a given model is included in this set only if the sales data revealed from prior pricing decisions makes it "probable". As a result, it gracefully transitions from being robust when demand model ambiguity is high to minimizing regret when this ambiguity diminishes upon receiving more data. We characterize the stochastic behavior of ARL's self-adapting ambiguity sets and derive a regret bound that highlights the link between the scale of revenue loss and the customer arrival pattern. We also show that ARL, by being conscious of both model ambiguity and revenue, bridges the gap between a distributionally robust policy and a follow-the-leader policy, which focus on model ambiguity and revenue, respectively. We numerically find that the ARL policy, or its extension thereof, exhibits superior performance compared to distributionally robust, follow-the-leader, and upper-confidence-bound policies in terms of expected revenue and/or value at risk.

Algorithmic Transparency with Strategic Users

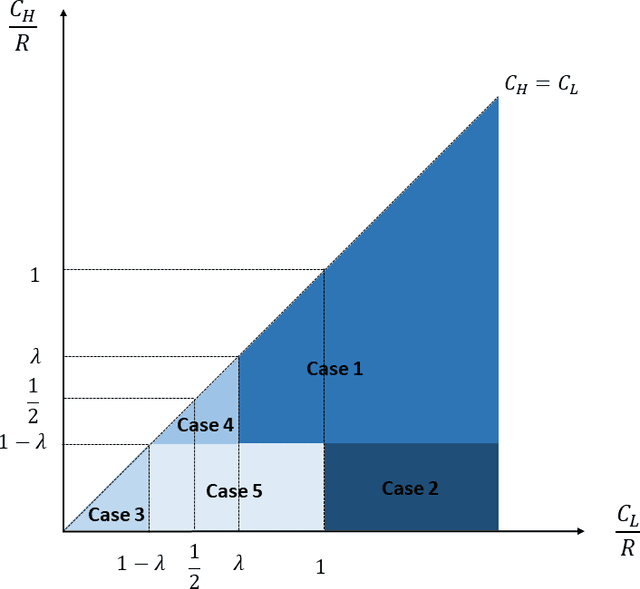
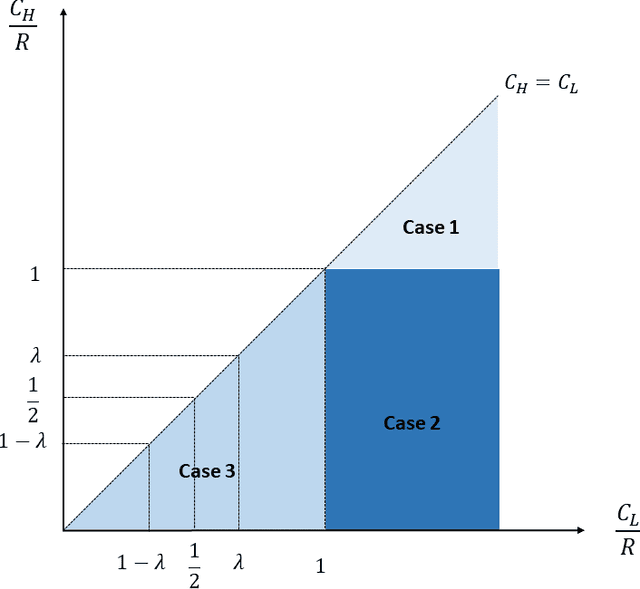
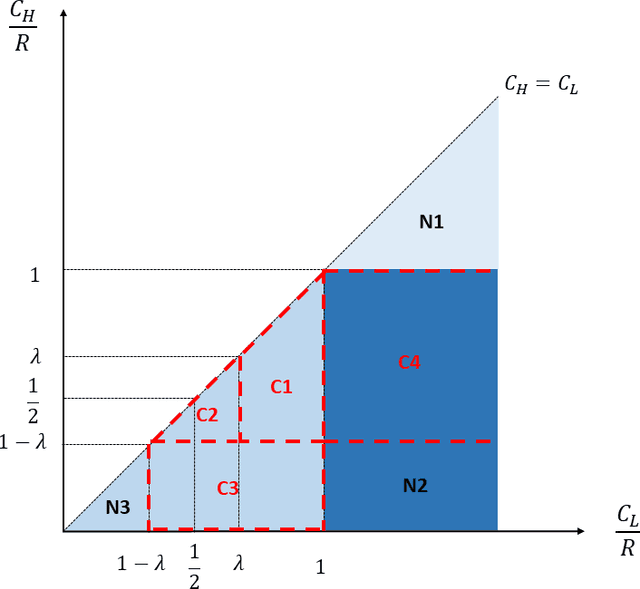
Should firms that apply machine learning algorithms in their decision-making make their algorithms transparent to the users they affect? Despite growing calls for algorithmic transparency, most firms have kept their algorithms opaque, citing potential gaming by users that may negatively affect the algorithm's predictive power. We develop an analytical model to compare firm and user surplus with and without algorithmic transparency in the presence of strategic users and present novel insights. We identify a broad set of conditions under which making the algorithm transparent benefits the firm. We show that, in some cases, even the predictive power of machine learning algorithms may increase if the firm makes them transparent. By contrast, users may not always be better off under algorithmic transparency. The results hold even when the predictive power of the opaque algorithm comes largely from correlational features and the cost for users to improve on them is close to zero. Overall, our results show that firms should not view manipulation by users as bad. Rather, they should use algorithmic transparency as a lever to motivate users to invest in more desirable features.