Boxiao Chen
Learning to Order for Inventory Systems with Lost Sales and Uncertain Supplies
Jul 10, 2022Abstract:We consider a stochastic lost-sales inventory control system with a lead time $L$ over a planning horizon $T$. Supply is uncertain, and is a function of the order quantity (due to random yield/capacity, etc). We aim to minimize the $T$-period cost, a problem that is known to be computationally intractable even under known distributions of demand and supply. In this paper, we assume that both the demand and supply distributions are unknown and develop a computationally efficient online learning algorithm. We show that our algorithm achieves a regret (i.e. the performance gap between the cost of our algorithm and that of an optimal policy over $T$ periods) of $O(L+\sqrt{T})$ when $L\geq\log(T)$. We do so by 1) showing our algorithm cost is higher by at most $O(L+\sqrt{T})$ for any $L\geq 0$ compared to an optimal constant-order policy under complete information (a well-known and widely-used algorithm) and 2) leveraging its known performance guarantee from the existing literature. To the best of our knowledge, a finite-sample $O(\sqrt{T})$ (and polynomial in $L$) regret bound when benchmarked against an optimal policy is not known before in the online inventory control literature. A key challenge in this learning problem is that both demand and supply data can be censored; hence only truncated values are observable. We circumvent this challenge by showing that the data generated under an order quantity $q^2$ allows us to simulate the performance of not only $q^2$ but also $q^1$ for all $q^1<q^2$, a key observation to obtain sufficient information even under data censoring. By establishing a high probability coupling argument, we are able to evaluate and compare the performance of different order policies at their steady state within a finite time horizon. Since the problem lacks convexity, we develop an active elimination method that adaptively rules out suboptimal solutions.
Self-adapting Robustness in Demand Learning
Nov 21, 2020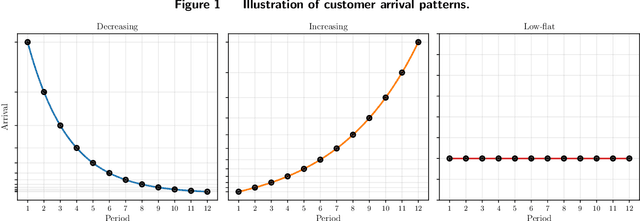
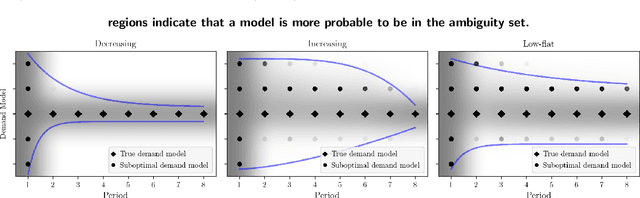
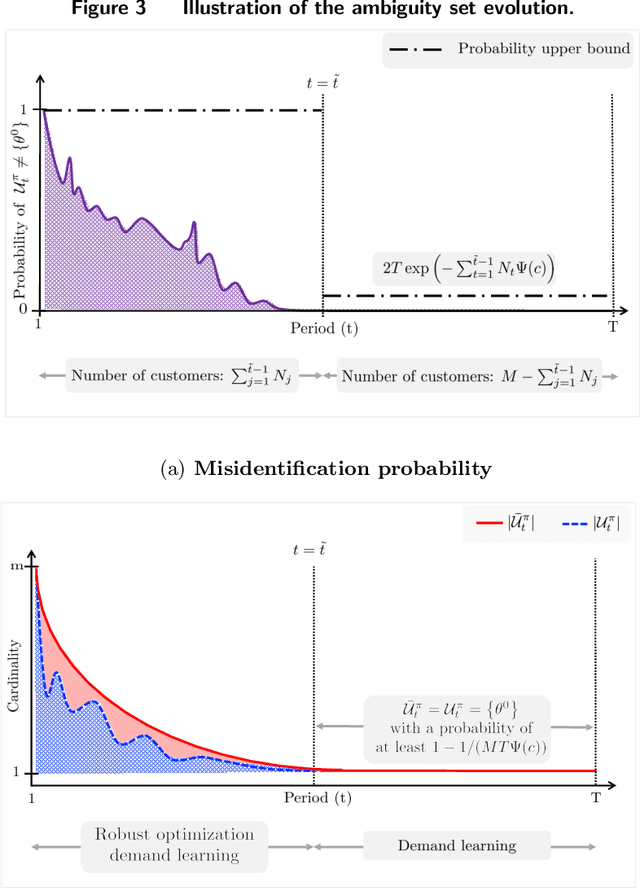
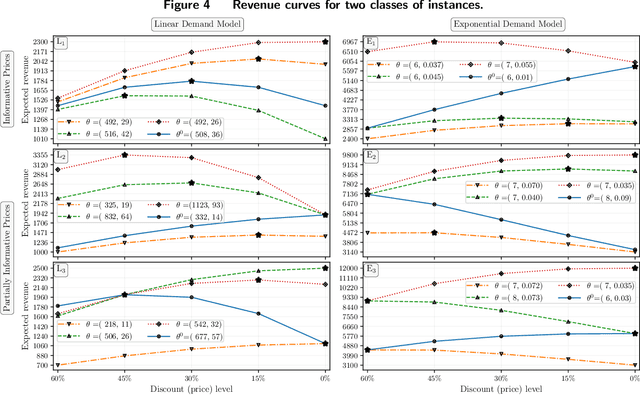
Abstract:We study dynamic pricing over a finite number of periods in the presence of demand model ambiguity. Departing from the typical no-regret learning environment, where price changes are allowed at any time, pricing decisions are made at pre-specified points in time and each price can be applied to a large number of arrivals. In this environment, which arises in retailing, a pricing decision based on an incorrect demand model can significantly impact cumulative revenue. We develop an adaptively-robust-learning (ARL) pricing policy that learns the true model parameters from the data while actively managing demand model ambiguity. It optimizes an objective that is robust with respect to a self-adapting set of demand models, where a given model is included in this set only if the sales data revealed from prior pricing decisions makes it "probable". As a result, it gracefully transitions from being robust when demand model ambiguity is high to minimizing regret when this ambiguity diminishes upon receiving more data. We characterize the stochastic behavior of ARL's self-adapting ambiguity sets and derive a regret bound that highlights the link between the scale of revenue loss and the customer arrival pattern. We also show that ARL, by being conscious of both model ambiguity and revenue, bridges the gap between a distributionally robust policy and a follow-the-leader policy, which focus on model ambiguity and revenue, respectively. We numerically find that the ARL policy, or its extension thereof, exhibits superior performance compared to distributionally robust, follow-the-leader, and upper-confidence-bound policies in terms of expected revenue and/or value at risk.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge