Efficient Generation of Molecular Clusters with Dual-Scale Equivariant Flow Matching

Amorphous molecular solids offer a promising alternative to inorganic semiconductors, owing to their mechanical flexibility and solution processability. The packing structure of these materials plays a crucial role in determining their electronic and transport properties, which are key to enhancing the efficiency of devices like organic solar cells (OSCs). However, obtaining these optoelectronic properties computationally requires molecular dynamics (MD) simulations to generate a conformational ensemble, a process that can be computationally expensive due to the large system sizes involved. Recent advances have focused on using generative models, particularly flow-based models as Boltzmann generators, to improve the efficiency of MD sampling. In this work, we developed a dual-scale flow matching method that separates training and inference into coarse-grained and all-atom stages and enhances both the accuracy and efficiency of standard flow matching samplers. We demonstrate the effectiveness of this method on a dataset of Y6 molecular clusters obtained through MD simulations, and we benchmark its efficiency and accuracy against single-scale flow matching methods.

Think While You Generate: Discrete Diffusion with Planned Denoising

Discrete diffusion has achieved state-of-the-art performance, outperforming or approaching autoregressive models on standard benchmarks. In this work, we introduce Discrete Diffusion with Planned Denoising (DDPD), a novel framework that separates the generation process into two models: a planner and a denoiser. At inference time, the planner selects which positions to denoise next by identifying the most corrupted positions in need of denoising, including both initially corrupted and those requiring additional refinement. This plan-and-denoise approach enables more efficient reconstruction during generation by iteratively identifying and denoising corruptions in the optimal order. DDPD outperforms traditional denoiser-only mask diffusion methods, achieving superior results on language modeling benchmarks such as text8, OpenWebText, and token-based generation on ImageNet $256 \times 256$. Notably, in language modeling, DDPD significantly reduces the performance gap between diffusion-based and autoregressive methods in terms of generative perplexity. Code is available at https://github.com/liusulin/DDPD.

Flow Matching for Accelerated Simulation of Atomic Transport in Materials

We introduce LiFlow, a generative framework to accelerate molecular dynamics (MD) simulations for crystalline materials that formulates the task as conditional generation of atomic displacements. The model uses flow matching, with a Propagator submodel to generate atomic displacements and a Corrector to locally correct unphysical geometries, and incorporates an adaptive prior based on the Maxwell-Boltzmann distribution to account for chemical and thermal conditions. We benchmark LiFlow on a dataset comprising 25-ps trajectories of lithium diffusion across 4,186 solid-state electrolyte (SSE) candidates at four temperatures. The model obtains a consistent Spearman rank correlation of 0.7-0.8 for lithium mean squared displacement (MSD) predictions on unseen compositions. Furthermore, LiFlow generalizes from short training trajectories to larger supercells and longer simulations while maintaining high accuracy. With speed-ups of up to 600,000$\times$ compared to first-principles methods, LiFlow enables scalable simulations at significantly larger length and time scales.

Generative Marginalization Models

We introduce marginalization models (MaMs), a new family of generative models for high-dimensional discrete data. They offer scalable and flexible generative modeling with tractable likelihoods by explicitly modeling all induced marginal distributions. Marginalization models enable fast evaluation of arbitrary marginal probabilities with a single forward pass of the neural network, which overcomes a major limitation of methods with exact marginal inference, such as autoregressive models (ARMs). We propose scalable methods for learning the marginals, grounded in the concept of "marginalization self-consistency". Unlike previous methods, MaMs support scalable training of any-order generative models for high-dimensional problems under the setting of energy-based training, where the goal is to match the learned distribution to a given desired probability (specified by an unnormalized (log) probability function such as energy function or reward function). We demonstrate the effectiveness of the proposed model on a variety of discrete data distributions, including binary images, language, physical systems, and molecules, for maximum likelihood and energy-based training settings. MaMs achieve orders of magnitude speedup in evaluating the marginal probabilities on both settings. For energy-based training tasks, MaMs enable any-order generative modeling of high-dimensional problems beyond the capability of previous methods. Code is at https://github.com/PrincetonLIPS/MaM.

Sparse Bayesian Optimization

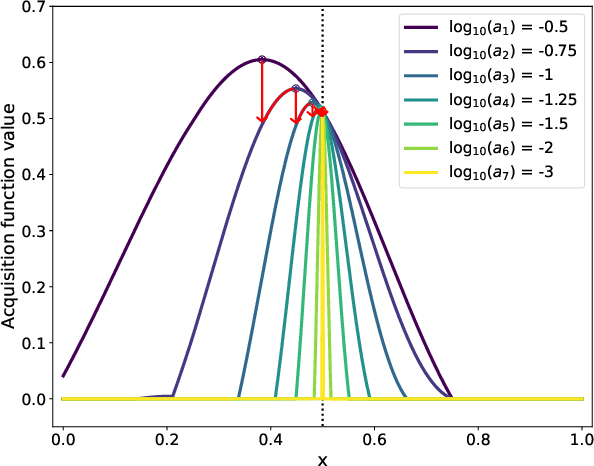
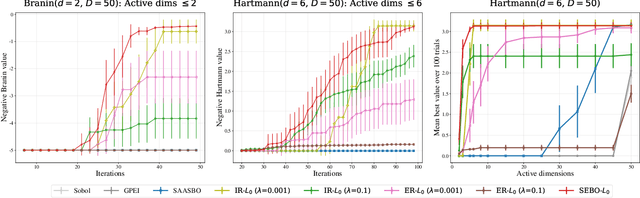
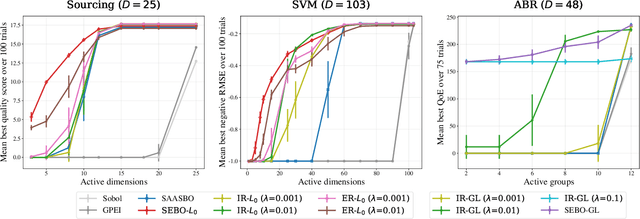
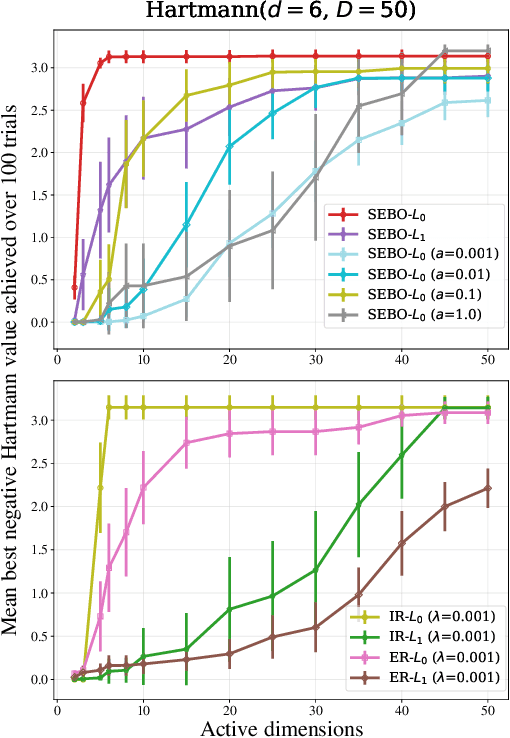
Bayesian optimization (BO) is a powerful approach to sample-efficient optimization of black-box objective functions. However, the application of BO to areas such as recommendation systems often requires taking the interpretability and simplicity of the configurations into consideration, a setting that has not been previously studied in the BO literature. To make BO applicable in this setting, we present several regularization-based approaches that allow us to discover sparse and more interpretable configurations. We propose a novel differentiable relaxation based on homotopy continuation that makes it possible to target sparsity by working directly with $L_0$ regularization. We identify failure modes for regularized BO and develop a hyperparameter-free method, sparsity exploring Bayesian optimization (SEBO) that seeks to simultaneously maximize a target objective and sparsity. SEBO and methods based on fixed regularization are evaluated on synthetic and real-world problems, and we show that we are able to efficiently optimize for sparsity.

ProBF: Learning Probabilistic Safety Certificates with Barrier Functions

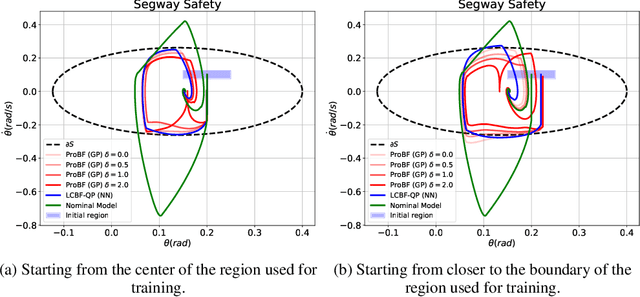
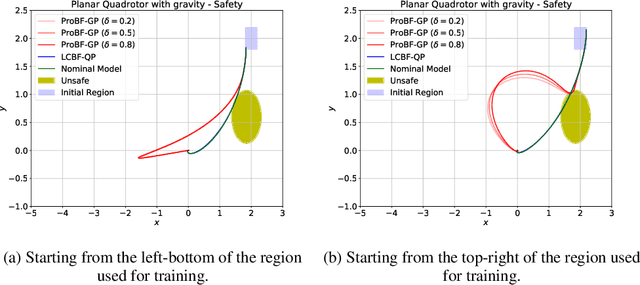
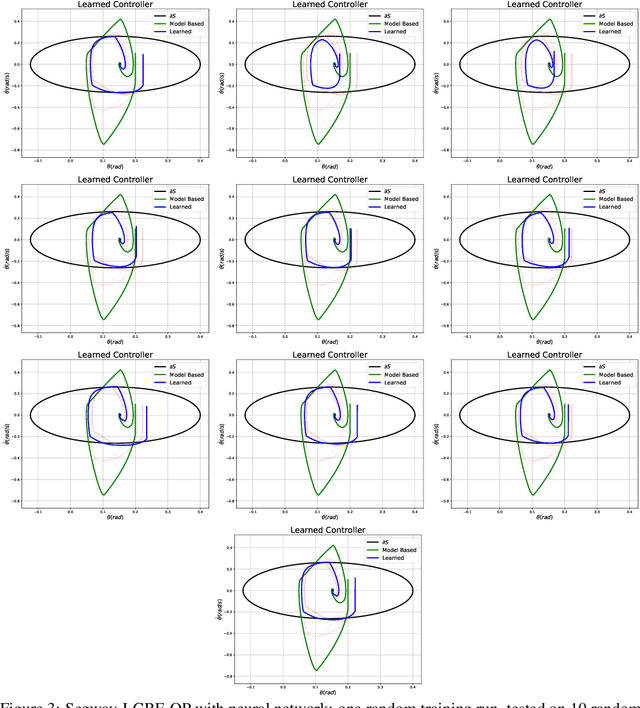
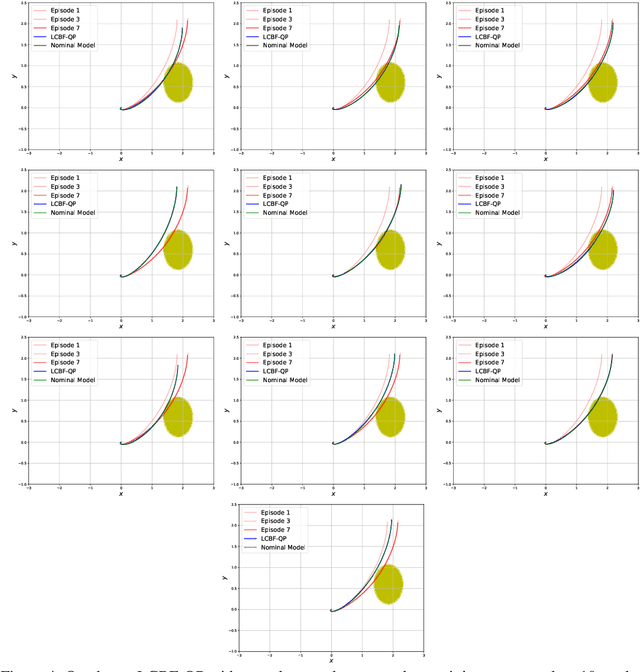
Safety-critical applications require controllers/policies that can guarantee safety with high confidence. The control barrier function is a useful tool to guarantee safety if we have access to the ground-truth system dynamics. In practice, we have inaccurate knowledge of the system dynamics, which can lead to unsafe behaviors due to unmodeled residual dynamics. Learning the residual dynamics with deterministic machine learning models can prevent the unsafe behavior but can fail when the predictions are imperfect. In this situation, a probabilistic learning method that reasons about the uncertainty of its predictions can help provide robust safety margins. In this work, we use a Gaussian process to model the projection of the residual dynamics onto a control barrier function. We propose a novel optimization procedure to generate safe controls that can guarantee safety with high probability. The safety filter is provided with the ability to reason about the uncertainty of the predictions from the GP. We show the efficacy of this method through experiments on Segway and Quadrotor simulations. Our proposed probabilistic approach is able to reduce the number of safety violations significantly as compared to the deterministic approach with a neural network.

The Landscape of Matrix Factorization Revisited

We revisit the landscape of the simple matrix factorization problem. For low-rank matrix factorization, prior work has shown that there exist infinitely many critical points all of which are either global minima or strict saddles. At a strict saddle the minimum eigenvalue of the Hessian is negative. Of interest is whether this minimum eigenvalue is uniformly bounded below zero over all strict saddles. To answer this we consider orbits of critical points under the general linear group. For each orbit we identify a representative point, called a canonical point. If a canonical point is a strict saddle, so is every point on its orbit. We derive an expression for the minimum eigenvalue of the Hessian at each canonical strict saddle and use this to show that the minimum eigenvalue of the Hessian over the set of strict saddles is not uniformly bounded below zero. We also show that a known invariance property of gradient flow ensures the solution of gradient flow only encounters critical points on an invariant manifold $\mathcal{M}_C$ determined by the initial condition. We show that, in contrast to the general situation, the minimum eigenvalue of strict saddles in $\mathcal{M}_{0}$ is uniformly bounded below zero. We obtain an expression for this bound in terms of the singular values of the matrix being factorized. This bound depends on the size of the nonzero singular values and on the separation between distinct nonzero singular values of the matrix.

Distributed Multi-Task Relationship Learning

Multi-task learning aims to learn multiple tasks jointly by exploiting their relatedness to improve the generalization performance for each task. Traditionally, to perform multi-task learning, one needs to centralize data from all the tasks to a single machine. However, in many real-world applications, data of different tasks may be geo-distributed over different local machines. Due to heavy communication caused by transmitting the data and the issue of data privacy and security, it is impossible to send data of different task to a master machine to perform multi-task learning. Therefore, in this paper, we propose a distributed multi-task learning framework that simultaneously learns predictive models for each task as well as task relationships between tasks alternatingly in the parameter server paradigm. In our framework, we first offer a general dual form for a family of regularized multi-task relationship learning methods. Subsequently, we propose a communication-efficient primal-dual distributed optimization algorithm to solve the dual problem by carefully designing local subproblems to make the dual problem decomposable. Moreover, we provide a theoretical convergence analysis for the proposed algorithm, which is specific for distributed multi-task relationship learning. We conduct extensive experiments on both synthetic and real-world datasets to evaluate our proposed framework in terms of effectiveness and convergence.